La estadística es la ciencia que se encarga de recopilar, organizar, procesar, analizar e interpretar datos con el fin de deducir las características de un grupo o población objetivo, su importancia radica en que es una fuente de información altamente confiable para la toma de decisiones.
En este post hallarás respuesta a las preguntas qué es estadística, cómo se define, cuál es su significado y sus partes. Además, aprenderás cuáles son los objetivos de esta ciencia, los tipos de estadística, descriptiva e inferencial (también llamada analítica o cuantitativa) y de lo que se ocupa cada una, ejemplificándolas de manera sencilla. Adicionalmente, encontrarás una breve reseña con la historia de esta ciencia, algunas definiciones de términos clave para iniciar su estudio y como cereza del pastel un curso compuesto por 13 video lecciones a través de las cuales te podrás adentrar al mundo de esta rama del saber. ¡Comencemos!
Qué es estadística, definición, significado y partes
La estadística es la ciencia de los datos, se ocupa de su recolección, organización, estructuración, análisis y presentación. Dichos datos se refieren a un fenómeno variable e incierto, por ejemplo el resultado de lanzar una moneda. Su aplicación busca inferir los principios que dirigen esos fenómenos, además, permite hacer predicciones y una toma de decisiones más informada.
Definición de estadística
A continuación la definición de estadística según algunos autores:
- Es la ciencia que estudia cómo debe emplearse la información y cómo dar una guía de acción en situaciones prácticas que entrañan incertidumbre. (Gutiérrez, p. 23)
- Es la ciencia de los datos, la cual implica su recolección, clasificación, síntesis, organización, análisis e interpretación, para la toma de decisiones frente a la incertidumbre (Ángel, p. 28)
- Es la rama del conocimiento humano que tiene como objeto el estudio de ciertos métodos inductivos aplicables a fenómenos susceptibles de expresión cuantitativa. (López, p. 1)
- Es el arte de aprender a partir de los datos. Está relacionada con la recopilación de datos, su descripción subsiguiente y su análisis, lo que nos lleva a extraer conclusiones. (Ross, p. 3)
- La estadística es la ciencia que trata de la recolección y descripción de las mediciones de muestras así como de las estimaciones y comparaciones poblacionales realizadas a partir de los resultados muestrales. (Romero, p. 25)
- Es una ciencia exacta cuyo objetivo fundamental es el estudio de diversas formas de comportamiento de la sociedad, para lo cual se fundamenta en el uso de diversos métodos y procedimientos matemáticamente demostrables de manera formal y rigurosa. (Cóndor, p. 10)
- Es una ciencia que facilita la toma de decisiones mediante la presentación ordenada de los datos observados en tablas y gráficos estadísticos, reduciendo los datos observados a un pequeño número de medidas estadísticas que permitirán la comparación entre diferentes series de datos y estimando la probabilidad de éxito que tiene cada una de las decisiones posibles. (Fernández et.al, p. 18)
Significado de Estadística
El Diccionario de la Lengua Española otorga el siguiente significado al término estadística:
- Estudio de los datos cuantitativos de la población, de los recursos naturales e industriales, del tráfico o de cualquier otra manifestación de las sociedades humanas.
- Rama de la matemática que utiliza grandes conjuntos de datos numéricos para obtener inferencias basadas en el cálculo de probabilidades.
Partes de la estadística
De acuerdo con Moore (p. XXXIV) la estadística, para su estudio, se divide en tres partes:
- La obtención de datos proporciona métodos para obtener datos que permiten dar respuestas claras a preguntas concretas,
- El análisis de datos se ocupa de los métodos y las ideas necesarias para organizar y describir datos utilizando gráficos y resúmenes numéricos.
- La inferencia estadística va más allá de los datos disponibles y obtiene conclusiones sobre un universo más amplio teniendo en cuenta la omnipresencia de la variabilidad y la incertidumbre de las conclusiones.
En el siguiente video se hace una corta introducción al concepto de estadística, se presenta una definición y, a través de un ejemplo, algunos conceptos adicionales que seguro te van a resultar útiles.
Objetivos de la estadística
1. Objetivo General
Como objetivo general se tiene que:
El objetivo de la estadística es mejorar la comprensión de hechos a partir de datos. (Moore, p. 267)
El principal objetivo de la estadística es hacer inferencias acerca de una población, con base en la información contenida en una muestra. (Pérez, p. 172)
2. Objetivos específicos
Algunos objetivos específicos son (Martínez, p. 9):
- Conocer la realidad de una observación o fenómeno.
- Determinar lo típico o normal de esa situación.
- Determinar los cambios que representa el fenómeno.
- Relacionar dos o más fenómenos.
- Determinar las causas que originan el fenómeno.
- Hacer estimaciones sobre el comportamiento futuro del fenómeno.
- Obtener conclusiones de un grupo menor (muestra) para hacerlas extensivas a un grupo mayor (población).
- Determinar el grado de validez y confiabilidad ya sea de las predicciones o las conclusiones obtenidas a partir de muestras.
Tipos de estadística
Básicamente se tienen dos tipos de estadística, a saber:
1. Estadística descriptiva
La estadística descriptiva se puede definir como un método para describir numéricamente conjuntos numerosos. Por tratarse de un método de descripción numérica, utiliza el número como medio para describir un conjunto, que debe ser numeroso, ya que las permanencias estadísticas no se dan en los casos raros. No es posible sacar conclusiones concretas y precisas de los datos estadísticos. (Vargas, p.33)
Objetivo
La finalidad última de la estadística descriptiva es resumir la información de conjuntos más o menos numerosos de datos. Para ello se asienta en un concepto inmediato a la tarea de recuento: la frecuencia, medida empírica de la ocurrencia de los distintos estados que puede presentar una variable. (SGT, p.16)
Ejemplo
Un docente de educación primaria desea conocer cuántos de los alumnos del curso que dirige saben cómo hacer operaciones aritméticas con el ábaco. Realizó una prueba a todos los estudiantes con la cual midió su grado de conocimientos en el uso de esta herramienta, así obtuvo datos que pudo representar en tablas y gráficos, además de calcular algunos indicadores con los cuales pudo apreciar que solo un 50% de sus discípulos contaba con los conocimientos requeridos para empezar el curso, por lo cual concluyó que lo mejor era impartir unas clases iniciales de nivelación para que todos estén en capacidad de aprovechar las lecciones.

Elementos de la estadística descriptiva. Fuente: Ramos et. al. (p. 16)
2. Estadística inferencial, analítica o deductiva
La estadística inferencial estudia la probabilidad de éxito de las diferentes soluciones posibles a un problema en las diferentes ciencias en las que se aplica y para ello utiliza los datos observados en una o varias muestras de la población. Mediante la creación de un modelo matemático infiere el comportamiento de la población total partiendo de los resultados obtenidos en las observaciones de las muestras. (Fernández et.al, p.17)
Objetivo
La inferencia estadística intenta tomar decisiones basadas en la aceptación o el rechazo de ciertas relaciones que se toman como hipótesis. Esta toma de decisiones va acompañada de un margen de error, cuya probabilidad está determinada. (Vargas, p.33)
La estadística inferencial tiene dos objetivos básicos: a) obtener conclusiones válidas acerca de una población sobre la base de una muestra, es decir, que las conclusiones que obtengamos de una muestra se puedan extrapolar a la población que dio origen a esa muestra y b) poder medir el grado de incertidumbre presente en dichas inferencias en términos de probabilidad. (Díaz, p.287)
Ejemplo
Un fabricante de colchones quiere conocer los hábitos de sueño de sus posibles clientes, para lo cual decide realizar una encuesta. Inicialmente establece una muestra de consumidores con el perfil requerido y procede a aplicarla, obteniendo así un conjunto de datos que le permiten inferir que una gran mayoría de usuarios prefieren los colchones blandos así que, para satisfacer al mercado, decide que empleará espumas de este tipo en la producción.
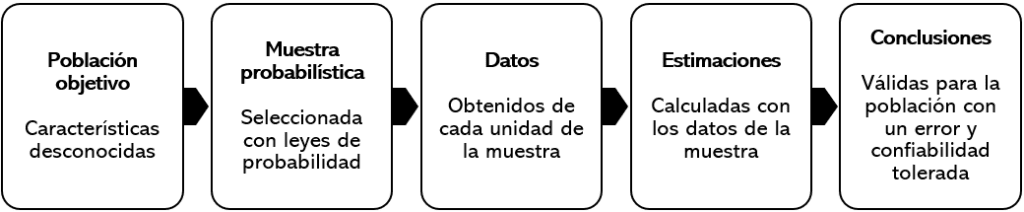
Elementos de la estadística inferencial. Fuente: Ramos et. al. (p. 17)
Breve reseña histórica
Hasta la actualidad se han desarrollado muchas y muy variadas técnicas estadísticas que se aplican en laboratorios y todo tipo de organizaciones por todo el mundo, en todos o casi todos los campos del conocimiento humano, lo que hace de la Estadística en sí misma una ciencia muy importante en el desarrollo de la vida.
A continuación algunos hitos históricos de su desarrollo (Llinás, p. 22 – 24):
El matemático británico Thomas Bayes (1702-1761) fue el pionero en el uso de la teoría de la probabilidad para argumentar desde lo particular a lo general o de la muestra a la población.
Pierre-Simon Laplace, astrónomo francés (1749-1827) admitió el principio de la probabilidad inversa, a él se debe el principio de que la distribución de una cantidad compuesta de partes independientes muestra toda una serie de características (la media, varianza y otras medidas) que son simplemente las sumas de cada característica de las distribuciones de las partes.
Carl Friedrich Gauss, matemático, astrónomo y físico alemán (1777-1855), se acercó al problema de la estimación estadística en forma empírica, planteando el problema de la estimación no solo en términos de probabilidades sino en términos de otros parámetros cuantitativos. Para este propósito trató de aplicar el método de máxima verosimilitud, aunque intentó derivar y justificar este método con el principio de la probabilidad inversa. Además, perfeccionó el ajuste sistemático de las fórmulas de regresión, simple y múltiple, por el método de los mínimos cuadrados, el cual, en los casos en los que sea apropiado, es un ejemplo particular del método de máxima verosimilitud.
Friedrich Robert Helmert, matemático y geólogo alemán (1843-1917), descubriría la distribución chi-cuadrada como una distribución de la varianza muestral para una distribución normal, pero como su obra fue escrita en alemán y desconocida en otras lenguas, luego se le atribuyó ese mismo descubrimiento a Karl Pearson, matemático y científico inglés (1857-1936), quién se considera que instituyó las disciplinas de la estadística matemática y de la bioestadística.
William Sealy Gosset, estadístico inglés (1876-1937), descubrió, a comienzos del Siglo XX, la forma de la distribución t mediante una combinación de trabajos empíricos y matemáticos con números aleatorios en su trabajo como estudiante y colaborador en el laboratorio de Pearson.
Ronald Fisher, estadístico y biólogo inglés (1890 – 1962), considerando uno de los padres de la inferencia estadística moderna, propuso y desarrolló el concepto de análisis de la varianza, los valores p, el método de máxima veroscimilitud, la distribución f (de Fisher, aunque también se le atribuye a otro científico, el estadounidense George W. Snedecor, quien la habría nombrado de esa manera por su gran admiración a Fisher), investigó la relación de los genes de diferentes características y desarrolló métodos de análisis multivariante para responder esas inquietudes.
Frank Yates, estadístico inglés (1902 – 1994), en su trabajo con Fisher, desarrolló la correccion de continuidad o correccion de Yates.
Egon Pearson, hijo de Karl, estadístico británico (1895 – 1980), y Jerzy Neyman, matemático y estadístico polaco (1894 – 1981), propusieron la prueba de hipótesis, en oposición a los estudios de Fisher, conocido como el lema fundamental de Neyman-Pearson, un resultado que describe el criterio óptimo para distinguir dos hipótesis simples.
Más sobre eventos históricos de esta ciencia en el siguiente video:
Elementos de la estadística
A continuación se definen algunos de los elementos más empleados en estadística:
- Población. Es el conjunto de todos los posibles elementos que intervienen en un experimento o en un estudio. La hay de dos tipos
- Población finita. Es aquella que indica que es posible alcanzarse o sobrepasarse al contar. Es aquella que posee o incluye un número limitado de medidas y observaciones.
- Población infinita. Es infinita si se incluye un gran conjunto de medidas y observaciones que no pueden alcanzarse en el conteo. Son poblaciones infinitas porque hipotéticamente no existe límite en cuanto al número de observaciones que cada uno de ellos puede generar.
- Muestra. Un conjunto de medidas u observaciones tomadas a partir de una población dada. Es un subconjunto de la población.
- Muestra representativa. Un subconjunto representativo seleccionado de una población de la cual se obtuvo.
- Muestreo. Al estudio de la muestra representativa.
- Censo. Al estudio completo de la población.
- Parámetro. Lo constituyen las características medibles en una población completa. Se le asigna un símbolo representado por una letra griega.
- Estadístico o estadígrafo. Es la medida de una característica relativa a una muestra. La mayoría de los estadísticos muestrales se encuentran por medio de una fórmula y suelen asignárseles nombres simbólicos que son letras latinas.
- Datos estadísticos (Variables). Los datos son agrupaciones de cualquier número de observaciones relacionadas. Para que se considere un dato estadístico debe tener 2 características: a) Que sean comparables entre sí. b) Que tengan alguna relación.
- Variable. Una característica que asume valores. Clases de datos:
- Variable cuantitativa o escalar. Será una variable cuando pueda asumir sus resultados en medidas numéricas.
- Variable cuantitativa discreta. Es aquella que puede asumir solo ciertos valores, números enteros. Ejemplo: El número de estudiantes (1,2,3,4)
- Variable cuantitativa continua. Es aquella que teóricamente puede tomar cualquier valor en una escala de medidas, ya sea entero o fraccionario. Ejemplo, Estatura: 1.90 m
- Variables cualitativas nominales. Cuando no es posible hacer medidas numéricas, son susceptibles de clasificación. Ejemplo: Color de autos: rojo, verde, azul.
- Experimento. Es una actividad planificada, cuyos resultados producen un conjunto de datos. Es el proceso mediante el cual una observación o medición es registrada. Ejemplo: ¿Cuál será la preferencia del consumidor ante dos marcas de refresco con similares características en un ambiente armónico y sin publicidad?
Video curso de estadística descriptiva
A continuación un curso de estadística descriptiva a través del cual podrás aprender los conceptos fundamentales de esta ciencia (José Luis Suárez, 13 videos)
Bibliografía
- Ángel Gutiérrez, Julio César. Estadística general aplicada. Universidad Eafit, 1998.
- Cóndor E., Ilmer. Teoría de la probabilidad y aplicaciones estadísticas.
- Díaz Narváez, Víctor. Metodología de la investigación científica y bioestadística. RIL Editores, 2009
- Fernández Fernández, Santiago; Cordero Sánchez, José María; Córdoba Largo, Alejandro; Cordero, José María. Estadística descriptiva, ESIC Editorial, 2002.
- Gutiérrez Cabria, Segundo. Filosofía de la estadística, Universitat de València, 1994.
- López Cazuzo, Rafael. Cálculo de probabilidades e inferencia estadística, Universidad Católica Andrés Bello, 2006.
- Llinás Solano, Humberto. Introducción a la estadística matemática. ECOE Ediciones, 2018.
- Martínez Bencardino, Ciro. Estadística básica aplicada, Ecoe Ediciones, 2012.
- Moore, David S. Estadística aplicada básica, Antoni Bosch editor, 2005.
- Pérez Tejada, Arnoldo Elorza. Estadística, ciencias sociales, del comportamiento y de la salud. Cengage Learning Editores, 2008.
- Ramos R. Julio, del Águila, Víctor y Bazalar B., Ana. Estadística básica para los negocios. Universidad de Lima, 2017.
- Romero Revilla, Félix. Aprendiendo estadística. Universidad Ricardo Palma, 2001.
- Ross, Sheldon M. Introducción a la estadística, Editorial Reverté, 2007.
- SGT. La estadística y la probabilidad en la Educación Secundaria Obligatoria, Ministerio de Educación, 2003.
- Vargas Sabadías, Antonio. Estadística descriptiva e inferencial, Universidad de Castilla La Mancha, 1996.
