Al hacer análisis estadísticos en busca de probar hipótesis, estos deben ser los apropiados según lo que se ha establecido, y lo que se ha construido a través del tiempo por diferentes autores en el mundo. Esta nota técnica se ha elaborado para disponer de una herramienta adecuada que oriente cómo proceder al momento de probar hipótesis utilizando variables cualitativas de tipo categóricas como son las nominales y ordinales. En esta se orienta al usuario, cómo proceder al momento de realizar la prueba de Chi Cuadrada para la prueba de hipótesis utilizando variables categóricas.
Contempla:
- Variables y tipos de pruebas.
- La chi cuadra.
Las Variables y los Tipos de Pruebas de Hipótesis
Cuando se hacen análisis estadísticos utilizando variables categóricas es importante conocer el tipo de análisis que se debe hacer y cómo se interpretan los resultados. Como se sabe, las variables se dividen en cualitativas (nominales y ordinales) y cuantitativas (intervalar y de razón).
En el caso de las variables categóricas, cuando se trata de probar hipótesis utilizando pruebas de contraste se pueden utilizar: Chi cuadrada (X2) de Pearson o Ji cuadrada, la prueba exacta de Fisher y la de Mcnemar (Statis Geek, 2019)
Tabla 1. Relación de variables y Tipos de Pruebas
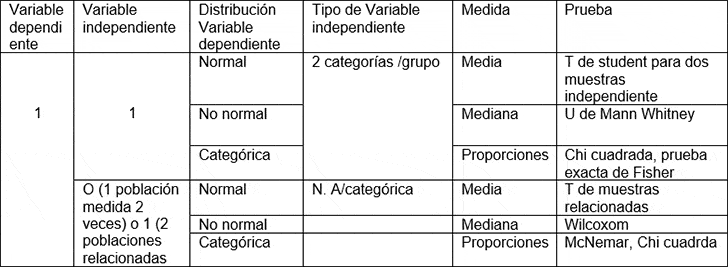
Fuente: Statis Geek (22 junio, 2019). Chi cuadra recuperado de https://www.youtube.com/watch?v=ruLCTkX4tRk
Chi Cuadrada
La prueba de chi cuadrada, es útil para establecer si existe o no relación entre variables categóricas (nominales, y ordinales). Se puede realizar mediante el uso de la fórmula siguiente:
![]()
Utilizando esta fórmula se puede trabajar en Excel, a partir de los datos observados que sirven de base para la prueba de asociación, además se pueden usar paquetes estadísticos que la contienen. Si dos variables están asociadas, significa que parte de la variabilidad de una de ella, puede ser explicada por la otra. Sin embargo, aunque esta prueba puede explicar la asociación entre dos variables, no explica las características o forma de la asociación.
Para entender los resultados de la Chi cuadrada es importante entender lo que es, la intensidad y el sentido o dirección de la asociación. La primera nos informa la fuerza de la asociación, que puede ir de débil a muy fuerte, y la segunda nos dice si es directa o inversa. Cuando la relación es directa, si aumenta una variable sube la otra, o viceversa. En cambio, si es inversa, si sube una variable baja la otra, o viceversa. Es importante destacar que esto solo es posible identificar si se trabaja con dos variables ordinales. Existe otro elemento que se puede determinar con la asociación de variables categóricas y es lo relativo al tipo de relación que existe entre las variables asociadas, que puede ser: simétrico y direccional (Ruiz, 2019).
- El simétrico, se usa cuando solo se desea medir la fuerza y sentido de la asociación entre dos variables categóricas. Ejemplo la intensidad de asociación entre el nivel de calificaciones y el método de enseñanza utilizado (una nominal y otra ordinal). En este caso hay un conjunto de pruebas que se puede utilizar.
- El direccional. Cuando se desea determinar, qué tanto una variable, puede ayudar a predecir el comportamiento de la otra. Para eso una de las variables debe ser dependiente (y) ante la otra independiente (x). por Ej. nivel de estrés (Y) con el nivel de la carrera (x). En este caso hay un conjunto de pruebas que lo pueden determinar.
La diferencia básica entre ambas, es que la simétrica solo permite medir la intensidad de la asociación, mientras que la de direccionalidad permite establecer el grado de predicción que se puede tener de una variable dependiente, conocimiento el nivel de la variable independiente (Ruiz, 2019).
Según Ruiz (2019) para la realización de la prueba chi cuadra se deben seguir los siguientes pasos:
- Identificación de las variables que se desean asociar.
- Identificar los tipos de variables que se desean asociar (nominales u ordinales). En este caso, pueden ser dos variables nominales, al menos una de ellas nominal, y dos variables ordinales.
- Establecer el tipo de relación que se desea realizar. En este sentido hay dos manera en que se pueden relacionar las variables que son:
- Medidas de simetría. Miden la relación de variables.
- Medidas de la direccionalidad. Mide la relación de dependencia entre dos variables (una dependiente y otra independiente).
En el caso de al menos una variable nominal se puede medir la intensidad de la relación. Mientras que si son dos variables ordinales, se puede medir la intensidad de la relación y la direccionalidad de esta.
- Identificar el tipo de prueba que se debe realizar.
- Si es una medida simétrica. Si se trabaja con dos variables nominales o al menos una variable nominal, se usa una escala de 0 a 1, que permite conocer la intensidad de la relación (no dependencia), una vez que previamente se ha determinado si existe asociación mediante el uso del P-valor (p-valor≤0.05 ó 0.01) según se halla definido previamente. Las pruebas disponibles en este caso son: Phi, V de Cramer, y Coeficiente de contingencia. Si en cambio se utilizan dos variables ordinales, en la medida simétrica se trabaja con una escala de -1 a +1 y se utilizan las pruebas: Gamma, Tau b de Kendall, y Tau C de Kendall (ver tabla 2)
- Si es una medida de direccionalidad. Si al menos se trabaja con una variable nominal, se usa una escala de 0 a 1, permite conocer la direccionalidad de la relación (grado de dependencia) y utiliza la prueba Lambda. En cambio cuando se trabaja con dos variables ordinales en la medida de direccionalidad se usa la escala de -1 a +1 y la prueba D de Somers.
Tabla 2. Medidas de Asociación para Variables Nominales
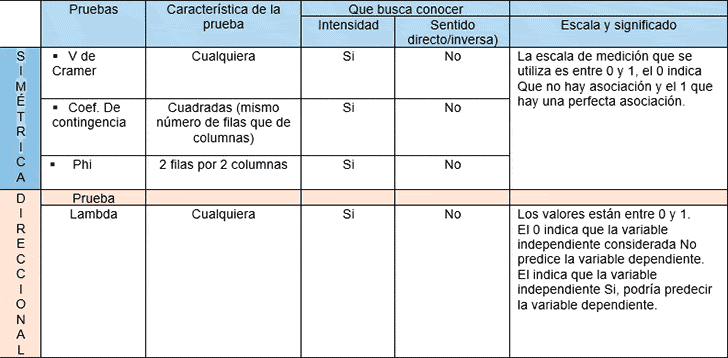
Nota: extraído de Ruiz, C. C. (12 de octubre de 2019). Chi cuadra y medidas de asociación. Recuperado el 31 de marzo de 2020, de https://www.youtube.com/watch?v=cyRAxn5NbD4&t=106s
Tabla 3. Tipo de asociación) V de Cramer)

Tabla 4. Medidas de Asociación Para variables Ordinales
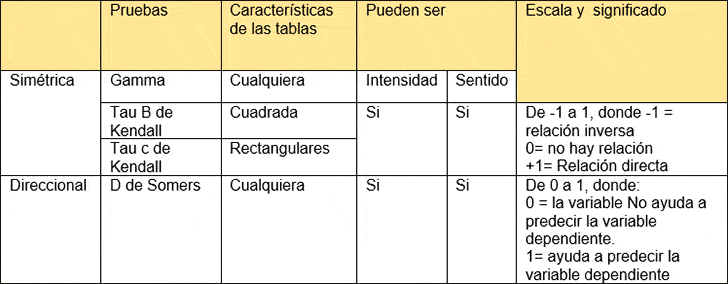
Nota. Statis Geek. (22 de junio de 2019). Chi cuadra. Recuperado el 2 de abril de 2020, de https://www.youtube.com/watch?v=ruLCTkX4tRk
Uso de Chi Cuadrada
Esta prueba se utiliza, cuando se desea establecer si existe o no asociación entre variables categóricas, como son las nominales y las ordinales.
Esta prueba contrasta una variable cualitativa Vs una variable cualitativa. La prueba se basa en la distribución de chi cuadrada para poder obtener un valor de P.
En la Chi cuadrada, la hipótesis nula (Ho) se expresa en término de independencia, mientras que la hipótesis alternativa o de investigación, se expresa en término de dependencia o asociación.
Supuestos de la Prueba Chi Cuadrada
Para la chi cuadrada, al menos el 80% de las frecuencias esperadas deben ser superior a 5. Para una prueba de 2*2, todos los valores esperados deben ser mayor a 5 para su uso. En caso de que el valor esperado sea menor a 5 se debe utilizar la prueba exacta de Fisher. Ej. Sexo (hombre, mujer), tipo de escuela (pública, privada).
Procedimiento de Chi Cuadrada
- Se calcula con la fórmula apropiada el SPSS, minitad etc.
- 2. Se interpretan los resultados de acuerdo a la hipótesis planteada y el nivel de significancia estadística considerada.
- Si la significancia en 5% el valor de p debe ser menos a 0.05 para rechazar la hipótesis nula.
- Si la significancia es del 1% el valor de p debe ser menor a 0.01 para rechazar la hipótesis nula.
- Si hay valores esperado menor de 5 en un 20% o más, no se usa Ji cuadrada sino la prueba exacta de Fisher.
- Si la tabla es 2*2 y tiene frecuencias esperadas menores a 5 se usa la prueba exacta de Fisher.
Te dejamos con un par de videos (que sirven como fuente de esta nota técnica) en los que podrás aprender más sobre la prueba chi cuadrada
Referencias
- Ruiz, C. C. (12 de octubre de 2019). Chi cuadra y medidas de asociación. Recuperado el 31 de marzo de 2020, de https://www.youtube.com/watch?v=cyRAxn5NbD4&t=106s
- Statis Geek. (22 de junio de 2019). Chi cuadra. Recuperado el 2 de abril de 2020, de https://www.youtube.com/watch?v=ruLCTkX4tRk


