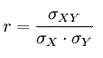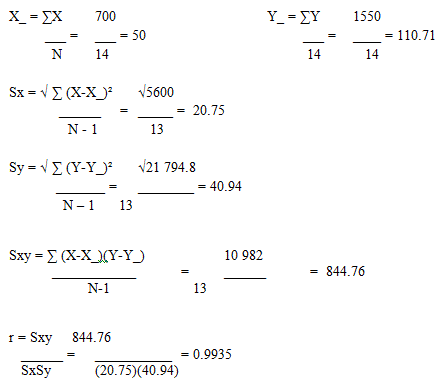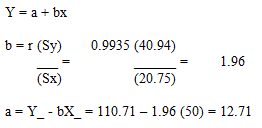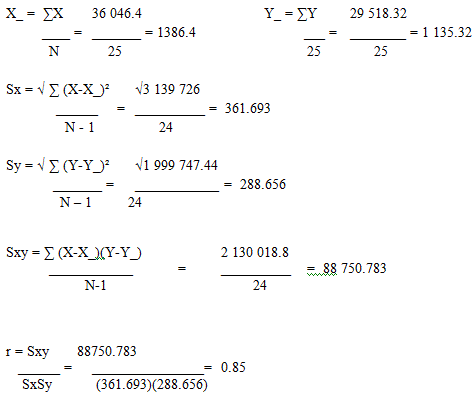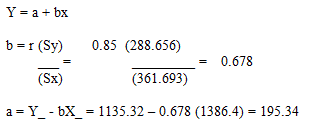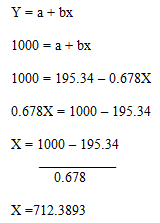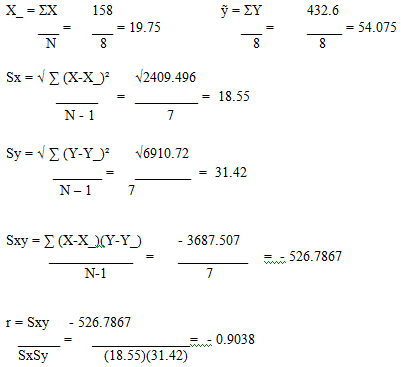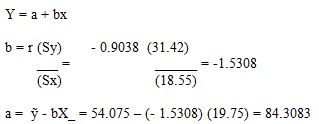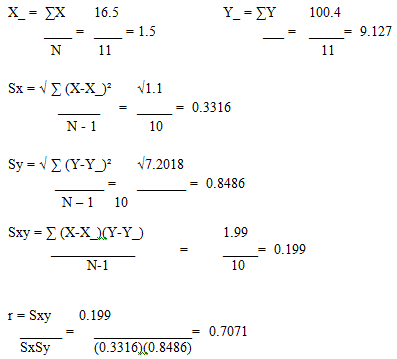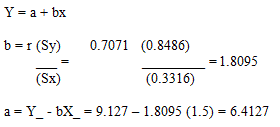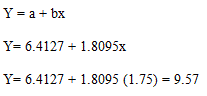Objetivo:
El objetivo de este proyecto es aprender a como usar el programa MINITAB y más que nada saber lo más posible de lo que es la probabilidad y estadística. Para ellos tenemos que hacer el siguiente proyecto que será publicado y mostrados a nuestros compañeros de clase y a aquellos que deseen verlo en la pagina de Internet www.gestiopolis.com. Todo lo que aprenderemos se lo debemos a nuestro maestro favorito que nos imparte la clase de Matemáticas III esperamos que nuestro proyecto sea de lo mas satisfactorio para nuestros videntes y leyentes y que no los decepcionemos. Sin más que decir o agregar nos despedimos con el siguiente proyecto que se les mostrara.
Antecedentes.
Variable
Una variable es un símbolo que representa un elemento no especificado de un conjunto dado. Dicho conjunto es llamado conjunto universal de la variable, universo o dominio de la variable, y cada elemento del conjunto es un valor de la variable. Sea x una variable cuyo universo es el conjunto {1,3,5,7,9,11,13}; entonces x puede tener cualquiera de esos valores: 1,3,5,7,9,11,13. En otras palabras x puede reemplazarse por cualquier entero positivo impar menor que 14. Por esta razón, a menudo se dice que una variable es un reemplazo de cualquier elemento de su universo.
Una variable es un elemento de una fórmula, proposición o algoritmo que puede adquirir o ser sustituido por un valor cualquiera (siempre dentro de su universo). Los valores que una variable es capaz de recibir, pueden estar definidos dentro de un rango, y/o estar limitados por criterios o condiciones de pertenencia, al universo que les corresponde (en estos casos, el universo de la variable pasa a ser un subconjunto de un universo mayor, el que tendría sin las restricciones).
Medición
La medición es la determinación de la proporción entre la dimensión o suceso de un objeto y una determinada unidad de medida. La dimensión del objeto y la unidad deben ser de la misma magnitud. Una parte importante de la medición es la estimación de error o análisis de errores.
Es comparar la cantidad desconocida que queremos determinar y una cantidad conocida de la misma magnitud, que elegimos como unidad. Teniendo como punto de referencia dos cosas: un objeto (lo que se quiere medir) y una unidad de medida ya establecida ya sea en Sistema Ingles, Sistema Internacional, o Sistema Decimal.
Al resultado de medir lo llamamos Medida.
Cuando medimos algo se debe hacer con gran cuidado, para evitar alterar el sistema que observamos. Por otro lado, no hemos de perder de vista que las medidas se realizan con algún tipo de error, debido a imperfecciones del instrumental o a limitaciones del medidor, errores experimentales, por eso, se ha de realizar la medida de forma que la alteración producida sea mucho menor que el error experimental que se pueda cometer.
La medida o medición es directa, cuando disponemos de un instrumento de medida que la obtiene, así si deseamos medir la distancia de un punto «A» a un punto «B», y disponemos del instrumento que nos permite realizar la medición.
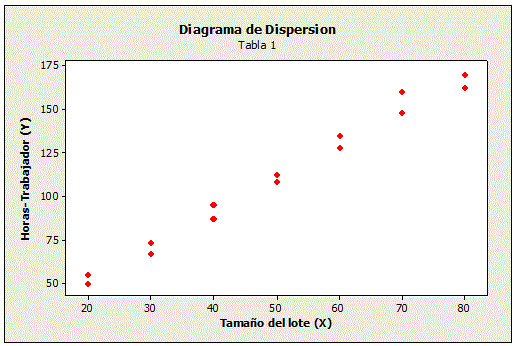
Diagrama de dispersión
Gráfica realizada trazando puntos en un plano coordenado de acuerdo con los valores pares observados para mostrar la relación entre dos variables.
Coeficiente de correlación de Pearson
El coeficiente de correlación de Pearson es un índice estadístico que mide la relación lineal entre dos variables cuantitativas. A diferencia de la covarianza, la correlación de Pearson es independiente de la escala de medida de las variables.
El cálculo del coeficiente de correlación lineal se realiza dividiendo la covarianza por el producto de las desviaciones estándar de ambas variables:
Siendo:
σXY la covarianza de (X,Y)
σX y σY las desviaciones típicas de las distribuciones marginales.
I.- Una compañía que fabrica partes para maquinaria quiere desarrollar un modelo para estimar el numero de horas – trabajador requeridas para corridas de producción de lotes de diversos tamaños. Se selecciona una muestra aleatoria de 14 corridas de producción (2 para cada tamaño de lote de 20, 30, 40, 50, 60, 70, 80) y se obtienen los siguientes resultados.
| Tamaño del lote (X) | Horas-Trabajador (Y) |
| 20 | 50 |
| 20 | 55 |
| 30 | 73 |
| 30 | 67 |
| 40 | 87 |
| 40 | 95 |
| 50 | 108 |
| 50 | 112 |
| 60 | 128 |
| 60 | 135 |
| 70 | 148 |
| 70 | 160 |
| 80 | 170 |
| 80 | 162 |
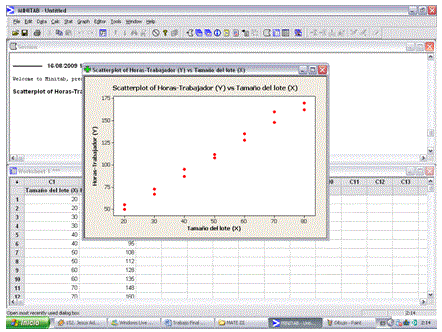
a) Grafique el Diagrama de Dispersión
b) Pronostique el número promedio de horas-trabajador requeridas para una corrida de producción de un lote de tamaño 100.
| Tamaño del lote (X) | Horas-Trabajador (Y) | (X-X_) | (X-X_)2 | (Y-Y_) | (Y-Y_)2 | (X-X_)(Y-Y_) |
| 20 | 50 | -30 | 900 | -60.71 | 3685.7 | 1821,3 |
| 20 | 55 | -30 | 900 | -55.71 | 3103.6 | 1671,3 |
| 30 | 73 | -20 | 400 | -37.71 | 1422.04 | 754,2 |
| 30 | 67 | -20 | 400 | -43.71 | 1910.56 | 874,2 |
| 40 | 87 | -10 | 100 | -23.71 | 562.16 | 237,1 |
| 40 | 95 | -10 | 100 | -15.71 | 246.8 | 157,1 |
| 50 | 108 | 0 | 0 | -2.71 | 7.34 | 0 |
| 50 | 112 | 0 | 0 | 1.29 | 1.66 | 0 |
| 60 | 128 | 10 | 100 | 17.29 | 298.94 | 172,9 |
| 60 | 135 | 10 | 100 | 24.29 | 590.004 | 242,9 |
| 70 | 148 | 20 | 400 | 37.29 | 1390.54 | 754,8 |
| 70 | 160 | 20 | 400 | 49.29 | 2429.5 | 985,8 |
| 80 | 170 | 30 | 300 | 59.29 | 3515.3 | 1778,7 |
| 80 | 162 | 30 | 300 | 51.29 | 2630.66 | 1538,7 |
| ?= 700 | ?= 1550 | ?= 5600 | ?= 21794.8 | ?= 10982 | ||
| X__ = 50 | Y_ = 110.71 |
X_ = Media de X Y_= Media de Y Sx = desviación estándar de X
Sy = desviación estándar de Y Sxy = Covarianza r =Coeficiente de correlación
Procedimiento de formulas y resultados:
Ecuación de la Regresión Lineal
b) Pronostique el número promedio de horas-trabajador requeridas para una corrida de producción de un lote de tamaño 100.
Y = a + bX
Y = 12.71 + 1.96X
Y = 12.71 + 1.96 (100) = 208.71
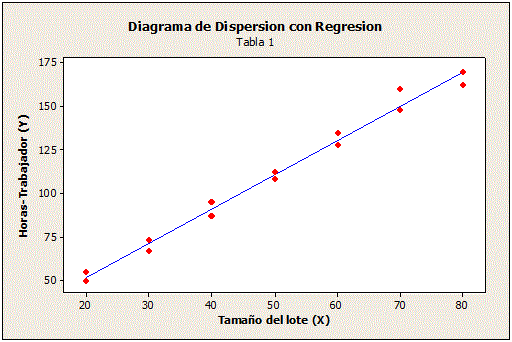
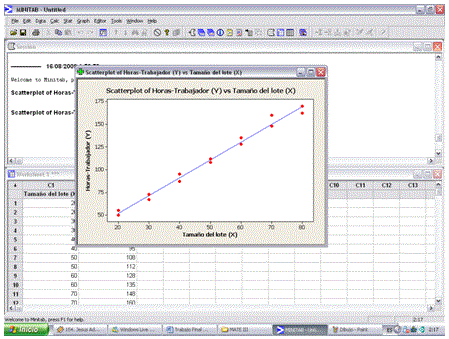
Diagrama de Dispersión con Regresión
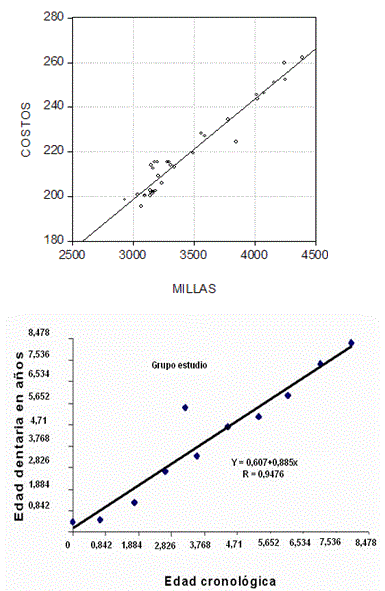
II.- Una compañía de bienes raíces residenciales en una ciudad grande desea poder predecir los costos mensuales de renta para departamentos, basada en el tamaño de los mismos definidos por los pies cuadrados de espacio. Se selecciona una muestra aleatoria y la información generada revela lo siguiente
| En dólares (X) | En pies cuadrados (Y) |
| 950 | 850 |
| 1600 | 1450 |
| 1200 | 1085 |
| 1500 | 1232 |
| 950 | 718 |
| 1700 | 1485 |
| 1650 | 1136 |
| 935 | 726 |
| 875 | 700 |
| 1150 | 956 |
| 1400 | 1100 |
| 1650 | 1285 |
| 2300 | 1985 |
| 1800 | 1369 |
| 1400 | 1175 |
| 1450 | 1225 |
| 1100 | 1245 |
| 1700 | 1259 |
| 1200 | 1150 |
| 1150 | 896 |
| 1600 | 1361 |
| 1650 | 1040 |
| 1200 | 755 |
| 800 | 1000 |
| 1750 | 1200 |
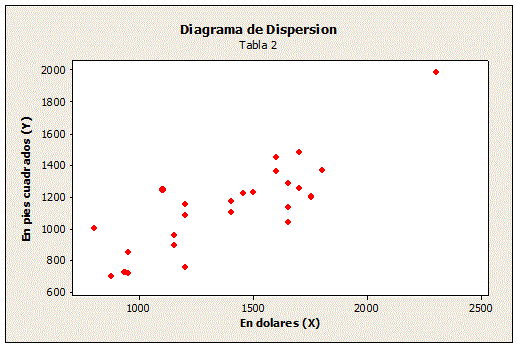
a) Grafique el Diagrama de Dispersión
b) Utilice el método de mínimos cuadrados para encontrar los coeficientes de regresión a y b.
c) Establezca la ecuación de regresión
d) Pronostique la renta mensual promedio para un departamento que tiene 1000 pies cuadrados.
| X | Y | X-X_ | (X-X_)2 | Y-Y_ | (Y-Y_)2 | (X-X_)(Y-Y_) |
| 950 | 850 | -436.4 | 190444.96 | -285.32 | 81407.5024 | 124513.648 |
| 1600 | 1450 | 213.6 | 45624.96 | 314.68 | 99023.5024 | 67215.648 |
| 1200 | 1085 | -186.4 | 34744.96 | -50.32 | 2532.1024 | 9379.648 |
| 1500 | 1232 | 113.6 | 12904.96 | 96.68 | 9347.0224 | 10982.848 |
| 950 | 718 | -436.4 | 190444.96 | -417.32 | 174155.982 | 182118.448 |
| 1700 | 1485 | 313.6 | 98344.96 | 349.68 | 122276.102 | 109659.648 |
| 1650 | 1136 | 263.6 | 69484.96 | 0.68 | 0.4624 | 179.248 |
| 935 | 726 | -451.4 | 203761.96 | -409.32 | 167542.862 | 184767.048 |
| 875 | 700 | -511.4 | 261529.96 | -435.32 | 189503.502 | 222622.648 |
| 1150 | 956 | -236.4 | 55884.96 | -179.32 | 32155.6624 | 42391.248 |
| 1400 | 1100 | 13.6 | 184.96 | -35.32 | 1247.5024 | -480.352 |
| 1650 | 1285 | 263.6 | 69484.96 | 149.68 | 22404.1024 | 39455.648 |
| 2300 | 1985 | 913.6 | 834664.96 | 849.68 | 721956.102 | 776267.648 |
| 1800 | 1369 | 413.6 | 171064.96 | 233.68 | 54606.3424 | 96650.048 |
| 1400 | 1175 | 13.6 | 184.96 | 39.68 | 1574.5024 | 539.648 |
| 1450 | 1225 | 63.6 | 4044.96 | 89.68 | 8042.5024 | 5703.648 |
| 1100 | 1245 | -286.4 | 82024.96 | 109.68 | 12029.7024 | -31412.352 |
| 1700 | 1259 | 313.6 | 98344.96 | 123.68 | 15296.7424 | 38786.048 |
| 1200 | 1150 | -186.4 | 34744.96 | 14.68 | 215.5024 | -2736.352 |
| 1150 | 896 | -236.4 | 55884.96 | -239.32 | 57274.0624 | 56575.248 |
| 1600 | 1361 | 213.6 | 45624.96 | 225.68 | 50931.4624 | 48205.248 |
| 1650 | 1040 | 263.6 | 69484.96 | -95.32 | 9085.9024 | -25126.352 |
| 1200 | 755 | -186.4 | 34744.96 | -380.32 | 144643.302 | 70891.648 |
| 800 | 1000 | -586.4 | 343864.96 | -135.32 | 18311.5024 | 79351.648 |
| 1750 | 1200 | 363.6 | 132204.96 | 64.68 | 4183.5024 | 23517.648 |
| ?= 36046.4 | ?= 29518.32 | ?= 3139726 | ?= 1999747.44 |
?= 2130018.8 |
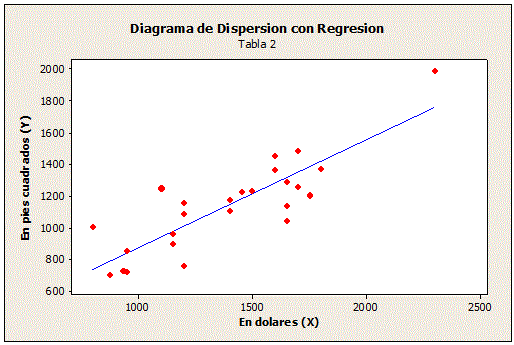
Ecuación de la Regresión Lineal
e) Pronostique la renta mensual promedio para un departamento que tiene 1000 pies cuadrados.
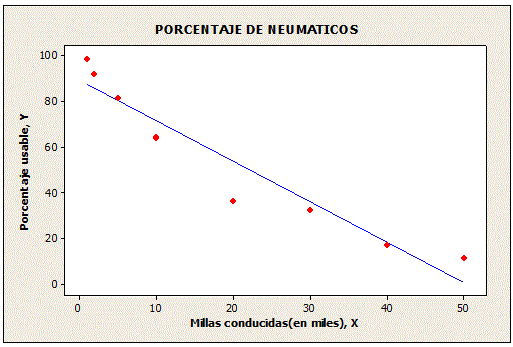
III.- Los siguientes datos se refieren al porcentaje de neumáticos radiales de alto rendimiento hechos por cierto fabricante que son aun usables después de haber sido empleados el número de millas indicadas.
Determine la ecuación de regresión que mejor ajuste los datos y determine el porcentaje usable para 25000 millas conducidas.
| Millas conducidas(en miles), X | Porcentaje usable, Y |
| 1 | 98.2 |
| 2 | 91.7 |
| 5 | 81.3 |
| 10 | 64.0 |
| 20 | 36.4 |
| 30 | 32.6 |
| 40 | 17.1 |
| 50 | 11.3 |
———-
| X | Y | (X-X_) | (X-X_)² | (y-?) | (y-?)² | (x-x_)(y-?) |
| 1 | 98.2 | -18.75 | 351.562 | 44.125 | 1947.015 | -827.343 |
| 2 | 91.7 | -17.75 | 315.062 | 37.625 | 1415.640 | -667.843 |
| 5 | 81.3 | -14.75 | 217.562 | 27.225 | 741.200 | -401.568 |
| 10 | 64.0 | -9.75 | 95.062 | 9.925 | 98.505 | -96.768 |
| 20 | 36.4 | 0.25 | 0.062 | -17.675 | 312.405 | -4.418 |
| 30 | 32.6 | 10.25 | 105.062 | -21.475 | 461.175 | -220.118 |
| 40 | 17.1 | 20.25 | 410.062 | -36.975 | 1367.150 | -748.743 |
| 50 | 11.3 | 30.25 | 915.062 | -23.825 | 567.630 | -720.706 |
|
?= 158 |
?= 432.6 |
?= 2409.496 |
?= 6910.72 |
?= – 3607.507 |
Ecuación de la Regresión Lineal
Determine la ecuación de regresión que mejor ajuste los datos y determine el porcentaje usable para 25000 millas conducidas.
Y = a + bx
Y = 23.85 + (-1.53)(25) = 46.0583
IV.- Se realiza un estudio sobre la cantidad de azúcar transformada en cierto proceso a varias temperaturas. Los datos se recolectan y registran como sigue:
| Temperatura (X) | Azúcar transformado (Y) |
| 1 | 8,1 |
| 1,1 | 7,8 |
| 1,2 | 8,5 |
| 1,3 | 9,8 |
| 1,4 | 9,5 |
| 1,5 | 8,9 |
| 1,6 | 8,6 |
| 1,7 | 10,2 |
| 1,8 | 9,3 |
| 1,9 | 9,2 |
| 2 | 10,5 |
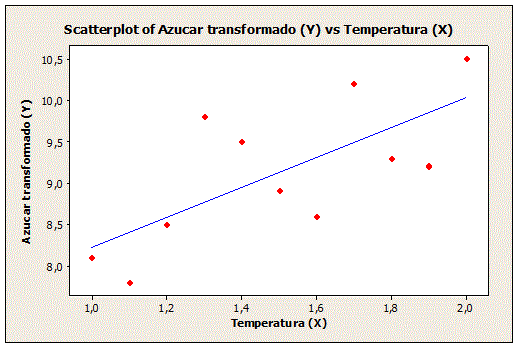
a) Estime la línea de regresión lineal.
b) Estime la cantidad media de azúcar transformada cuando la temperatura codificada es 1.75
| Temperatura (X) | Azúcar transformado (Y) | X-X_ | (X-X_)2 | Y-Y_ | (Y-Y_)2 | (X-X_)(Y-Y_) |
| 1 | 8,1 | -0,5 | 0,25 | -1,0272 | 1,0552 | 0,5136 |
| 1,1 | 7,8 | -0,4 | 0,16 | -1,3272 | 1,7616 | 0,5309 |
| 1,2 | 8,5 | -0,3 | 0,09 | -0,6272 | 0,3934 | 0,1881 |
| 1,3 | 9,8 | -0,2 | 0,04 | 0,6727 | 0,4525 | -0,1345 |
| 1,4 | 9,5 | -0,1 | 0,01 | 0,3727 | 0,1389 | -0,0372 |
| 1,5 | 8,9 | 0 | 0 | -0,2272 | 0,0516 | 0 |
| 1,6 | 8,6 | 0,1 | 0,01 | -0,5272 | 0,2780 | -0,0527 |
| 1,7 | 10,2 | 0,2 | 0,04 | 1,0727 | 1,1507 | 0,2145 |
| 1,8 | 9,3 | 0,3 | 0,09 | 0,1727 | 0,0298 | 0,0518 |
| 1,9 | 9,2 | 0,4 | 0,16 | 0,0727 | 0,0052 | 0,0290 |
| 2 | 10,5 | 0,5 | 0,25 | 1,3727 | 1,8843 | 0,6863 |
| ?= 16,5 | ?= 100,4 | ?= 1,1 | ?= 7,2018 | ?= 1,99 | ||
| X_=1,5 | X_=9,127 |
Ecuación de la Regresión Lineal
b) Estime la cantidad media de azúcar transformada cuando la temperatura codificada es 1.75
———-
Solución en MINITAB
Los siguientes pasos son con los que podremos hacer una tabla de datos, graficas, formulas y de mas cosas de probabilidad y estadística con el programa MINITAB. Las imágenes y procedimientos siguientes son los que usaremos para hacer una grafica de dispersión:
Paso 1.- Abrir MINITAB
Paso 2.- Colocarse en la pantalla principal
Paso 3.- Colocar los Datos que se desean obtener en las tablas. Por ejemplo la tabla de Tamaño de lote (X) y Horas-Trabajador (Y).
Paso 4.- Obtener el Diagrama de dispersión con los siguientes pasos:
4.1.- Abrir menú Graph
4.2.- Seleccionar Scatterplot y hacer clic.
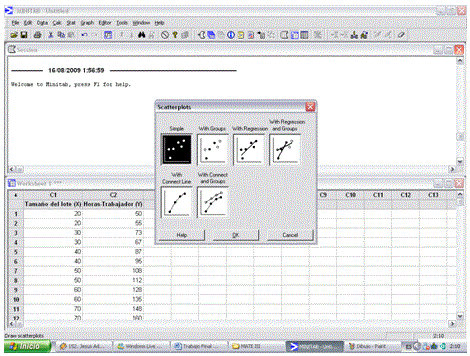
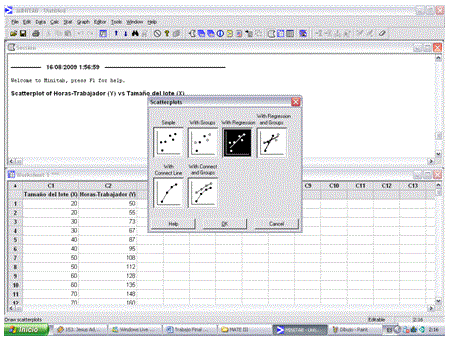
4.3.- Ya que se hizo clic aparecerá una ventana que dice scatterplots, seleccionar el modelo simple y hacer clic en ok.
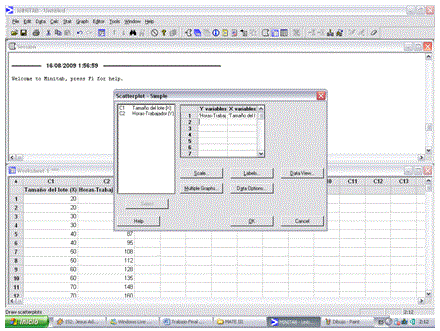
4.4.- Aparecerá otra ventana para colocar las variables “X” y “Y”, cuando aparezca esa ventana colocar las variables en las columnas correspondientes como se muestra en la siguiente imagen:
4.5.- Hacer clic en ok y se mostrara la grafica de dispersión.
Nota: si se quiere un diagrama de dispersión con la línea de regresión solo seleccionar scatterplot with regression y hacer los pasos ya siguientes ya mencionados como se muestra en la siguiente imagen:
Diagrama de dispersión con regresión lineal.
Experiencias de Aprendizaje:
La experiencia que obtuvimos al realizar el trabajo final fue algo buena y mala por los siguientes motivos.
Fue buena porque:
• Nos enseño a trabajar más en equipo y a esforzarnos cada vez más en nuestros trabajos.
• Siempre nos brindo la confianza para aclarar nuestras dudas.
• Impartió su clase con un dominio y gusto que la verdad a muchos profesores les falta.
• Siempre se porto muy respetuoso ante la clase.
La verdad lo único malo que podemos destacar fue la presión que sentimos todos los alumnos ya que están cerca los exámenes y la mayoría de los maestros encargaban trabajos finales con un alto porcentaje de calificación, por otra parte tratamos de dar lo mejor de nosotros para cumplir con las expectativas del maestro al momento de entregar el trabajo y pasar con buena calificación.
Conclusiones:
Todo el equipo estuvimos de acuerdo en lo siguiente:
Nos gusto mucho como nos impartió la materia de Matemáticas III ya que siempre nos
Tuvo demasiada paciencia al momento de explicar su plan de estudio.
También cabe destacar que fue en realidad uno de los mejores maestros que nos han impartido clase, por la razón de que siempre llegaba con demasiado entusiasmo para impartir su materia. Eso a nosotros nos motivo para esforzarnos más en su materia.
La verdad es un ejemplo a seguir por enseñarnos a ver con muy buena actitud la rama de matemáticas y no como una materia tan pesado y/o difícil.
Bueno es todo por el momento y agradecerle por todo este tiempo que nos impartió con muy buenas actitudes su materia, esperando que nuestra amistad siga perdurando aunque usted en un futuro no nos diera clases en la Universidad.
Bibliografía:
www.wikipedia.com
Material didáctico entregado por el profesor
Apuntes del cuaderno