Una línea de espera es el efecto resultante en un sistema cuando la demanda de un servicio supera la capacidad de proporcionar dicho servicio. Este sistema está formado por un conjunto de entidades en paralelo que proporcionan un servicio a las transacciones que aleatoriamente entran al sistema. Dependiendo del sistema que se trate, las entidades pueden ser cajeras, máquinas, semáforos, grúas, etcétera, mientras que las transacciones pueden ser: clientes, piezas, autos, barcos, etcétera. Tanto el tiempo de servicio como las entradas al sistema son fenómenos que generalmente tienen asociadas fuentes de variación que se encuentran fuera del control del tomador de decisiones, de tal forma que se hace necesaria la utilización de modelos estocásticos que permitan el estudio de este tipo de sistemas.
Una línea de espera puede modelarse como un proceso estocástico en el cual la variable aleatoria se define como el número de transacciones en el sistema en un momento dado; el conjunto de valores que puede tomar dicha variable es {O, 1, 2, . . . , N\ y cada uno de ellos tiene asociada una probabilidad de ocurrencia.
Objetivo
El objetivo es determinar qué nivel de servicio, ya sea por cantidad de entidades o por la velocidad de ellas, proporcionar para minimizar el costo total del sistema. Este costo está formado tanto por costo de servicio como por el que causa la espera.
Estructura de un sistema de línea de espera
Línea de espera de un solo canal
Cada cliente debe pasar por un canal, una estación para tomar y surtir el pedido, para colocar el pedido, pagar la cuenta y recibir el producto. Cuanto llegan más clientes forman una línea de espera y aguardan que se desocupe la estación para tomar y surtir el pedido.
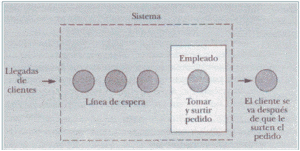
Línea de espera de un solo canal
Distribución de llegadas
Para determinar la distribución de probabilidad para la cantidad de llegadas en un período dado, se puede utilizar la distribución de Poisson.
/= Media o cantidad promedio de ocurrencia en un intervalo
e= 2.17828
X= cantidad de ocurrencias en el intervalo
Distribución de llegadas
El tiempo de servicio es el tiempo que pasa un cliente en la instalación una vez el servicio ha iniciado.
Se puede utilizar la distribución de probabilidad exponencial para encontrar la probabilidad de que el tiempo de servicio sea menor o igual que un tiempo t.
e= 2.17828
μ= cantidad media de unidades que pueden servirse por período
Disciplina de la línea de espera
Manera en la que las unidades que esperan el servicio se ordenan para recibirlo.
El primero que llega, primero al que se le sirve
Último en entrar, primero en salir
Atención primero a la prioridad más alta
Operación de estado estable
Generalmente la actividad se incrementa gradualmente hasta un estado normal o estable. El período de comienzo o principio se conoce como período transitorio, mismo que termina cuando el sistema alcanza la operación de estado estable o normal.
Modelos de línea de espera de un solo canal con llegadas de poisson y tiempos de servicio exponenciales
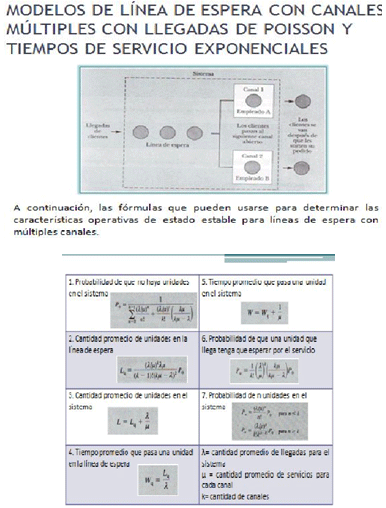
A continuación, las fórmulas que pueden usarse para determinar las características operativas de estado estable para una línea de espera de un solo canal.
El objetivo de las fórmulas es mostrar cómo se puede dar información acerca de las características operativas de la línea de espera.
Fórmulas
¿Cómo se puede mejorar la operación de línea de espera?
Características operativas para el sistema con la tasa media de servicio aumentada a μ=1.25 clientes por minuto.
Características operativas para el sistema
Modelos de línea de espera con canales múltiples
Valores de P0 para líneas de espera de canales múltiples
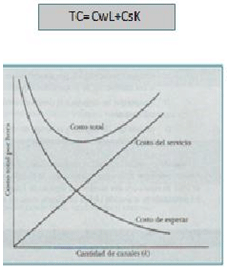
Análisis económico de las líneas de espera
Antes de que pueda llevarse a cabo un análisis económico de una línea de espera, debe elaborarse un modelo de costo total, el cual incluye el costo de esperar y el costo de servicio.
Cw= costo de esperar por período para cada unidad
L= cantidad promedio de unidades en el sistema
Cs= costo de servicio por período para cada canal
K= cantidad de canales
La forma general de las curvas de costo en el análisis económico de las líneas de espera consiste en que el costo del servicio aumenta conforme aumenta la cantidad de canales; pero con más canales, el servicio es mejor. Como resultado, el tiempo de espera y el costo disminuyen conforme se aumenta la cantidad de canales. Puede encontrarse la cantidad de canales que proporcionará una buena aproximación al diseño de costo total mínimo evaluando el costo total para varias alternativas de diseño.
Análisis económico de las líneas de espera
Programación lineal
Introducción
La programación lineal es una técnica matemática relativamente reciente (sigloXX), que consiste en una serie de métodos y procedimientos que permiten resolver problemas de optimización en el ámbito, sobre todo, de las Ciencias Sociales.
Nos centraremos en este tema en aquellos problemas simples de programación lineal, los que tienen solamente 2 variables, problemas bidimensionales.
Para sistemas de más variables, el procedimiento no es tan sencillo y se resuelven por el llamado Método Simplex (ideado por G.B.Danzig, matemático estadounidense en 1951).
Recientemente (1984) el matemático indio establecido en Estados Unidos, Narenda Karmarkar, ha encontrado un algoritmo, llamado algoritmo de Karmarkar, que es más rápido que el método simplex en ciertos casos. Los problemas de este tipo, en el que intervienen gran número de variables, se implementan en ordenadores.
La programación lineal constituye un importante campo de la optimización por varias razones, muchos problemas prácticos de la investigación de operaciones pueden plantearse como problemas de programación lineal.
Algunos casos especiales de programación lineal, tales como los problemas de flujo de redes y problemas de flujo de mercancías se consideraron en el desarrollo de las matemáticas lo suficientemente importantes como para generar por si mismos mucha investigación sobre algoritmos especializados en su solución.
Una serie de algoritmos diseñados para resolver otros tipos de problemas de optimización constituyen casos particulares de la más amplia técnica de la programación lineal. Históricamente, las ideas de programación lineal han inspirado muchos de los conceptos centrales de la teoría de optimización tales como la dualidad, la descomposición y la importancia de la convexidad y sus generalizaciones.
Del mismo modo, la programación lineal es muy usada en la microeconomía y la administración de empresas, ya sea para aumentar al máximo los ingresos o reducir al mínimo los costos de un sistema de producción. Algunos ejemplos son la mezcla de alimentos, la gestión de inventarios, la cartera y la gestión de las finanzas, la asignación de recursos humanos y recursos de máquinas, la planificación de campañas de publicidad, etc.
Otros son:
- Optimización de la combinación de cifras comerciales en una red lineal de distribución de agua.
- Aprovechamiento óptimo de los recursos de una cuenca hidrográfica, para un año con afluencias caracterizadas por corresponder a una determinada frecuencia.
- Soporte para toma de decisión en tiempo real, para operación de un sistema de obras hidráulicas;
- Solución de problemas de transporte.
Pasos para resolver un problema de programación lineal
- Elegir las incógnitas.
- Escribir la función objetivo en función de los datos del problema.
- Escribir las restricciones en forma de sistema de inecuaciones.
- Averiguar el conjunto de soluciones factibles representando gráficamente las restricciones.
- Calcular las coordenadas de los vértices del recinto de soluciones factibles (si son pocos).
- Calcular el valor de la función objetivo en cada uno de los vértices para ver en cuál de ellos presenta el valor máximo o mínimo según nos pida el problema (hay que tener en cuenta aquí la posible no existencia de solución si el recinto no está acotado).
Ejemplo de programación lineal
Unos grandes almacenes encargan a un fabricante pantalones y chaquetas deportivas.
El fabricante dispone para la confección de 750 m de tejido de algodón y 1000 m de tejido de poliéster. Cada pantalón precisa 1 m de algodón y 2 m de poliéster. Para cada chaqueta se necesitan 1.5 m de algodón y 1 m de poliéster.
El precio del pantalón se fija en 50 € y el de la chaqueta en 40 €.
¿Qué número de pantalones y chaquetas debe suministrar el fabricante a los almacenes para que éstos consigan una venta máxima?
1Elección de las incógnitas.
x = número de pantalones
y = número de chaquetas
2Función objetivo.
f(x,y)= 50x + 40y
Referencias:
Reza, Mohamad. García, Eduardo. Simulación y análisis de modelos estocásticos. McGraw Hill. (Líneas de espera)
