Una decisión en el presente, puede afectar toda una vida en el futuro. Partiendo de la premisa anterior y trasladándolo al campo empresarial, esta mantiene relación gráfica muy parecida a lo que se vive todos los días en las oficinas de la alta gerencia, con los jefes departamentales, incluso con todos los que tienen la capacidad en la organización de decidir situaciones críticas en el desempeño del ejercicio empresarial de toda compañía.
Las decisiones son fundamentales y siempre requieren de acciones rápidas, por ello se ha recurrido a la modelación matemática como una herramienta que coadyuve en la identificación de las mejores decisiones y de este modo, con toda la seguridad que se ha descartado todo sesgo, tomarse la decisión en base a un fundamento cuantificable y calificable.
En el presente escrito, se describe de manera general la terminología y conceptualización de modelación matemática, las implicaciones que tiene en la toma de decisiones y se mencionan los modelos mayormente aplicados en base a los requerimientos de las organizaciones ante la dinámica de los sistemas. Se describen los modelos matemáticos más comúnmente utilizados.
Conceptualización
- Modelo
“Un modelo es una representación de un objeto, sistema o idea, de forma diferente al de la entidad misma. El propósito de los modelos es ayudarnos a explicar, entender o mejorar un sistema. Un modelo de un objeto puede ser una réplica exacta de éste o una abstracción de las propiedades dominantes del objeto” (Universidad Nacional Autónoma de Colombia, 2015)
La naturaleza del hombre siempre ha sido la necesidad de conocer el comportamiento de su medio para crear a partir de ello un proceso que le ayude a manipularlo según su necesidad o conveniencia y para ello se vale de la modelación. En efecto:
- Modelar- es el proceso mediante el cual se crean modelos con vistas a investigar la realidad.
- Modelación- es crear una representación explícita del entendimiento que una persona tiene de una situación, o simplemente de las ideas que se tienen acerca de una situación.
Proceso de la toma de decisiones
Es el proceso de la toma de decisiones que le da la razón de ser e identidad a la organización en el que interesa el proceso de elección que resulta en la acción, una dinámica donde el decidir y hacer es parte de toda la administración.
En este contexto (Simon, 1964) describe que la gestión administrativa debe incluir en las tareas de decidir y hacer, principios de organización que aseguren una toma de decisiones correcta de igual manera que debe incluir principios que aseguren una acción efectiva.
Por ello es que en la toma de decisiones no se pueden aislar los eventos iniciales o básicos del comportamiento y perspectiva humana.
Básicamente en la incertidumbre de la elección el decisor determinará una opción de un conjunto de varias después de un proceso detallado y pormenorizado de las alternativas resultantes.
Algunos elementos distintos que ayudan al decisor en su elección racional enuncian:
- Se debe tener un conocimiento profundo del tema en el que será decisor.
- Ejecuta un orden jerárquico de preferencias del conjunto de todas las alternativas con que cuenta.
- El decisor no tiene restricción de capacidad para el procesamiento de la información.
- No queda objeción a las alternativas equivalentes.
A partir de estos principios y su formación profesional, el decisor posee el conocimiento y las habilidades para analizar y valorar la información que como resultado produzcan la toma de la mejor decisión fundamentada.
“La fórmula de toma de decisiones en la organización ha creado una nueva forma de pensamiento acerca de cómo operan realmente las organizaciones, aumentando nuestra comprensión del diseño organizacional” (Morgan, 1980)
Dinámica del entorno
Las decisiones en las organizaciones no debieran considerarse como patrones establecidos, sino siempre contemplar que están en continuo cambio, esto quiere decir que si se toma una buena decisión en el presente, mañana quizás no sea la correcta, lo que implica que el análisis debe considerarse dinámico, en continua revisión.
Es cierto que los modelos y algoritmos catalizan los análisis, pero esto no determina una solución al continuo cambio, por lo tanto una forma de hacer frente y como estrategia al tiempo, estratégicamente se determina diseñar modelos matemáticos a diferentes niveles y secuencias de tiempo.
El Dr. Flores Cantú en su investigación sobre Métodos y modelado matemático para el análisis de procesos complejos en las organizaciones, menciona al menos cuatro niveles en los se enfoca la toma de decisiones mediante el uso de modelos matemáticos.
A continuación se hace una breve descripción de cada uno de ellos:
- Nivel estratégico.- aquí es donde se toman las decisiones sobre los objetivos de la organización. Para ello requiere del conocimiento del contexto y proceso a través de análisis de histórico de datos. Con decisiones a largo plazo y estas están enfocadas a los niveles directivos.
- Nivel de planeación.- son las decisiones enfocadas a los recursos que se encuentran en toda la planta y están disponibles en cualquier momento, lo que posibilita acciones estratégicas. El tiempo relativamente es corto pues las decisiones se toman en períodos entre tres a cuatro semanas.
- Nivel de programación.- refiere esencialmente a la asignación de tareas para que se ejecute en nivel anterior. El tiempo es un recurso. En si la planeación determina el cómo se ejecutan las acciones. Con un periodo entre por día o hasta semanal.
- Nivel de ejecución.- es el nivel de mayor dinamismo, en sí su tarea es la supervisión de cumplimiento de normas y programas. Esto porque lo planeado no siempre ocurre como se espera y en necesario mantener alerta para reaccionar inmediatamente el cambio.
Sistema
“Los sistemas están formados por partes que son puestas en funcionamiento juntas de una forma particular para obtener un objetivo” (Kafati, 2009)
En los sistemas en importante mencionar que es más importante las relaciones internas que los elementos individuales.
Dinámica del sistema
Aquel sistema que no presenta cambios se le considera “determinístico”. La gran mayoría los sistemas son dinámicos; es decir, cambian a través de tiempo en base a un comportamiento, cuando este sigue una ruta específica, entonces se dice que presenta un patrón de comportamiento.
Entonces será dinámico o estático según el enfoque que se busque y de acuerdo a las variables que se determinen, referimos variable a todo aquello que cambia dentro del sistema.
Dentro de los modelos estáticos o determinísticos, las decisiones son consideradas de acuerdo a los resultados. En contraparte cuando a esto se le añade el nivel de riego, entonces se traslada a un modelo probabilístico.
Gutiérrez Kafati refiere mediante un ejemplo la diferencia entre un modelo determinístico y un probabilístico, donde establece considerar el pasado y el futuro de la siguiente manera: “Nada que hagamos ahora puede cambiar el pasado, pero cualquier cosa que hacemos influencia y cambia el futuro, a pesar de que el futuro tiene un elemento de incertidumbre”.
Concluyendo que los CEO se ocupan más de pronosticar el futuro con cierto nivel de incertidumbre, que considerar el histórico pasado.
Métodos matemáticos
En función a lo que ya se desarrolló, entonces se establece que cada problema requiere de su propia solución a partir de uno o diferentes métodos matemáticos. No es posible etiquetar determinadas soluciones para x problemas.
No obstante se pueden apreciar tendencias entre los métodos los cuales dan un valor agregado según la problemática que enfrentan. Algunos métodos de matemáticos comúnmente utilizados son:
- Técnicas de Modelos matemáticos
Hay una extensa cantidad de recursos de modelación matemática y cada una de ellas está en base a lo que se quiere analizar. Cada modelo tiene sus propias características y en base a ello factores específicos inmerso en el proceso.
Por lo que en este proceso se pueden llegar a considerar los cuatro niveles de la toma de decisiones en los que se sugiere cuáles son los de utilidad.
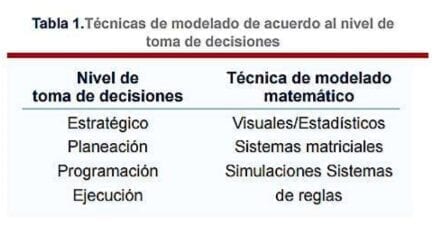
Modelado de Toma de Decisiones
- Técnica de visualización
Considera todos aquellos modelos basados gráficamente por medio de ordenadores, se prioriza en los modelos de visualización. Así el diseño correcto y ajustado a las necesidades se considera útil en el proceso de la toma de decisiones.
- Optimización matemática
Comúnmente al estudio de los algoritmos corresponde la programación matemática.
Cada tipo de algoritmo está diseñado para cumplir con determinados requerimientos, mientras que los modelos algebraicos o diferenciales pueden utilizar otro tipo de programación en base a sus necesidades.
- Heurísticos.
Este tipo de técnica es muy utilizada para optimización y se utiliza cuando la estructura de los modelos no es apropiada. La gran diferencia entre los heurísticos es que no brindan una solución matemática al programa, cuando no hay un algoritmo matemático.
Los heurísticos a pesar de sus restricciones pueden ofrecer soluciones útiles cuando no se sabe de algoritmos matemáticos conocidos.
- Sistemas expertos
En palabras generales, los sistemas expertos buscan montar sobre un existente un sistema de decisiones automatizados basado en el conocimiento avanzado del ser humano. Por su complejidad requieren inversión de tiempo en el diseño y capacitación, además de colaboración estrecha con expertos en la materia. Se hace uso de ellos cuando se requiere automatizar decisiones en el nivel jerárquico de ejecución.
- Análisis y minera de datos
Diseñar modelos siempre requiere de conocimientos sólidos y profundos en los procesos involucrados. Normalmente lo adquirimos a partir de la expedida de experto que ha dedicado tiempo de su vida a la investigación y análisis, a través de libros, revistas, periodos, publicaciones. Sin embargo la materia prima de estos modelos se alimenta básicamente del histórico de datos.
El propósito del análisis es la obtención de datos del histórico para la creación de los modelos que sustenten en la toma de decisiones.
Uso de modelos matemáticos para la toma de decisiones
Los modelos matemáticos y la toma de decisiones después de todo no están tan dispersos uno del otro. Ambos reaccionan en consecuencia a las eventualidades de las organizaciones para evaluar su desempeño.
Es imprescindible que toda organización fomenta a partir de su toma de decisiones, sin importar el nivel de organización, los que tienen una responsabilidad interna dentro de la compañía el uso de modelación matemática para obtener los resultados esperados.
La toma de decisiones por lo tanto no es un proceso que debe incorporar a una actividad más en la apretada agenda de los directivos, sino que debe estudiarse con cautela y poder determinar las mejores y óptimas decisiones que afectarán a toda la organización.
Conclusión
Las organizaciones, sea grandes o pequeñas esta regidas una misma premisa; la toma de decisiones. Parece ser un tema común y que no representa más que un poco de la atención de los responsables de las organizaciones, sin embargo, el papel que juega la toma de decisiones es elemental y vital en el funcionamiento y permanencia.
Una pequeña decisión puede marcar el rumbo de toda una organización. Y a partir de ello es que tan pronto como los directivos identificaron que las estrategias pueden mejorar, comenzaron a explorar áreas o aplicaciones hasta ese momento desconocidas en el campo de las matemáticas.
De este modo surge el estudio de la toma de decisiones a partir de modelos matemáticos, los cuales se aproximaban más, o por lo menos proporcionan un panoramas más amplio del futuro cercano.
Referencias
- Cantú, H. R. (2013). Métodos y modelado matemático para el análisis de procesos complejos en las organizacione. CELERINET, 64-69.
- García, J. (2006). Monografias.com. Obtenido de La modelación, los modelos y su importancia para las ciencias de la educación: http://www.monografias.com/trabajos36/los-modelos/los-modelos.shtml
- Kafati, E. G. (01 de Mayo de 2009). Pensamiento imaginativo . Obtenido de Modelamiento matemático para la toma de decisiones:
- http://manuelgross.bligoo.com/content/view/501562/Modelamientomatematico-para-la-toma-de-decisiones.html
- Morgan, G. (1980). Imágenes de la Organización. Madrid : Roma .
- Munévar, A. H. (2008). Atlantic International University . Obtenido de Toma de decisiones :
- http://www.aiu.edu/publications/student/spanish/TOMA%20DE%20DECISIO NES%20-%20Decisions%20Making.html#_Toc145505545
- SALGADO, C. A. (2006). Propuesta de un modelo matemático multicriterio, para que la toma de decisiones en fondos de empleados y cooperativas de trabajo asociado de manizales coadyuve a la coopetitividad . Manizales.
- Simon, H. A. (1964). El Comportamiento Administrativo. Estudio de los procesos decisorios en la organización administrativa. Valencia.
- Universidad Nacional Autónoma de Colombia. (2015). Obtenido de Facultad de Administración: http://www.virtual.unal.edu.co/cursos/sedes/manizales/4060010/lecciones/C apitulo1/modelo.htm


