Sin duda alguna la toma de decisiones es una de las situaciones más difíciles a las que se enfrenta el ser humano, la mayoría de los profesionistas al tomar una decisión busca argumentar cuantitativamente, lógicamente bajo el pensamiento matemático.
Los cursos de matemáticas impartidos en la escuela, apoyan en diversas áreas de conocimiento, no obstante se enfocan principalmente en la resolución de problemas propios de esta materia, es por esto que al ubicarlas en planes de estudio de diversas disciplinas, puede ser complicada su modelación, esta ciencia debiera tener un propósito más amplio y profundo que sólo ser un apoyo instrumental para el planteamiento y solución de problemas; otro de sus objetivos debería ser el desarrollo del pensamiento lógico.
DESARROLLO
DEFINICIONES
El pensamiento lógico es aquel que se desprende de las relaciones entre los objetos y procede de la propia elaboración del individuo. Surge a través de la coordinación de las relaciones que previamente ha creado entre los objetos. (DE, s.f.)
Un modelo matemático se define como una descripción desde el punto de vista de las matemáticas, es aquel que emplea algún tipo de formulismo matemático para expresar relaciones, proposiciones sustantivas de hechos, variables, parámetros, entidades y relaciones entre variables y/o entidades u operaciones, para estudiar comportamientos de sistemas complejos ante situaciones difíciles de observar en la realidad. (VALDIVIA, 2013)
PENSAMIENTO LÓGICO
La lógica representa la base fundamental para el desarrollo de las matemáticas. Podemos afirmar que, a su vez, las matemáticas permiten el desarrollo de pensamiento lógico. Esta última afirmación requiere distinguir el tipo de lógica de la que hablamos. Si se piensa en una lógica formal, como tradicionalmente la conocemos, donde el cumplimiento de formas y reglas para dar validez a las conclusiones es irrestricto, los caminos construidos a través de las matemáticas pueden volverse camisas de fuerza para el desarrollo del libre del pensamiento y de la capacidad de aprender a aprender.
Por el contrario, consideramos que la lógica que sustenta el propósito de las matemáticas como instrumento para el desarrollo del aprendizaje reflexivo es la lógica dialéctica, en la que los conceptos que parecen contrapuestos y contradictorios, como concreto-abstracto, análisis-síntesis, inducción, deducción, entre otros; no son uno la negación del otro sino más bien los elementos duales que inducen hacia la dinámica de pensamiento necesaria para descubrir, interpretar y generar nuevo conocimiento.
TIPOS DE DECISIONES COMPLEJAS
En primer lugar, la clasificación por nivel distingue tres tipos de decisiones que dependen de la posición jerárquica del decisor. Estas decisiones son: estratégicas o de planificación, tácticas o de pilotaje y operacionales o de regulación. Sus principales características son: (DAROS)
1- Decisiones estratégicas o de planificación.
- Los decisores son los altos directivos.
- Se remiten a la selección de fines, objetivos generales y planes a largo plazo.
- La información debe ser oportuna y de calidad. Un error puede ser fatal.
Ejemplos: localización, recursos financieros, productos a fabricar, etc.
2- Decisiones tácticas o de pilotaje.
- Los decisores son los directivos intermedios.
- Es la puesta en práctica de las decisiones estratégicas.
- Son útiles para repartir eficientemente los recursos limitados.
3- Decisiones Operacionales o de regulación
Ejemplos: distribución en planta, presupuesto, producción, etc.
- Decisiones operacionales o de regulación.
- Los decisores son los ejecutivos más inferiores: supervisores y gerentes.
- Se refieren a las actividades funcionales y rutinarias, al día a día.
Ejemplos: aceptación o rechazo de créditos, inventario, asignación de trabajos, etc.
La clasificación por métodos se realiza dependiendo del procedimiento utilizado para elegir la alternativa final, las diferentes decisiones son:
1- Decisiones programadas
- Se define un procedimiento o criterio de forma que estas decisiones no tengan que tratarse de nuevo cada vez que surjan.
- Hacen frente a los problemas estructurados, bien definidos y rutinarios.
- Se pueden definir, predecir y analizar los elementos del problema y sus relaciones.
- Su resolución se realiza utilizando hábitos, costumbres, procedimientos estandarizados, heurísticos y/o simulación.
Ejemplo: un cliente presenta una queja para la que se pone en marcha un protocolo de compensación, la realización de tareas rutinarias recogidas en el manual de procedimientos, etc.
2- Decisiones no programadas
- Son decisiones nuevas, no estructuradas e inusualmente importantes.
- No hay métodos preestablecidos para tratar estos sucesos inesperados.
- Para su resolución se utiliza la intuición, creatividad o criterio personal del decisor.
Ejemplos: una catástrofe natural destruye uno de los almacenes de la empresa y se debe decidir su reparación o su localización en otro lugar, una empresa quiere dar el salto al mercado internacional, etc.
Finalmente, se propone una clasificación sintética basada en las dos anteriores, es decir, en función del nivel jerárquico donde se tome la decisión y del método utilizado, distinguiendo entre decisiones estructuradas, semiestructuradas y no estructuradas
1- Decisiones estructuradas (decisiones programadas)
- Las tres fases principales (inteligencia, diseño y elección) son estructuradas.
- Se usan métodos matemáticos y reglas de decisión en todas las fases.
2- Decisiones semiestructuradas
- Imposibilidad de usar métodos en la fase de inteligencia e incluso en la de diseño y selección.
- Generalmente la fase de inteligencia no es estructurada, pero en ella, una vez identificado el problema, es posible el uso de modelos matemáticos, de algoritmos o de reglas de decisión.
3- Decisiones no estructuradas (no programadas)
- No se pueden utilizar métodos matemáticos o reglas de ningún tipo.
- Ninguna de las fases es estructurada.
PROCESO DE TOMA DE DECISIONES
La toma de decisiones es el proceso que consiste en escoger una entre varias opciones.
- LA TEORÍA PRESCRIPTIVA Es un método normativo que define y trata de explicar la forma en que se deben tomar las decisiones. Propone los pasos que se deben seguir para tomar buenas decisiones y los puntos clave que se deben tomar en cuenta.
- LA TEORÍA DESCRIPTIVA Se ocupa de describir cómo se toman en realidad las decisiones, las cuáles sufren muchas veces la influencia de factores subjetivos tales como la personalidad del individuo o la presión de la situación. (BOREA, 2002)
La forma en que las personas que dirigen las organizaciones, deben llegar a una decisión (teoría prescriptiva) y la forma en que lo hacen finalmente (teoría descriptiva) pueden ser muy diferentes.
A la hora de establecer los pasos dentro del proceso de toma de decisiones existe diversidad de criterios por varios autores y en ocasiones coinciden con las etapas.
A continuación se presenta una metodología científica en la toma de decisiones. (MACHADO, 2016)
1- Observación de la realidad:
En este primer paso se define el problema en relación con los objetivos propuestos y que están implicados en el mismo, y se identifican por abstracción los factores que influyen en los objetivos.
2- Representación en un modelo:
Una vez identificados los factores, se seleccionan los que son más relevantes, no teniendo en cuenta aquellos cuya influencia sea mínima. En esta fase se formulan las alternativas y los demás factores del ambiente estructural.
3- Prueba y verificación del modelo:
El modelo explica de una manera útil aunque no del todo exacta lo que está implicado en el problema en relación con los objetivos propuestos. Sin embargo, no debe tomarse una decisión hasta que el modelo no haya sido probado mediante una contrastación adecuada En general, la verificación dependerá del tipo de contraste elegido y del modelo elaborado.
4- Desarrollo de una regla de decisión:
Una vez realizada la verificación con resultados satisfactorios, entonces el modelo puede ser utilizado en la toma de decisiones. Sin embargo, es preciso tener en cuenta que es el mejor mientras el sistema para el cual ha sido elaborado no se modifique. Por lo tanto, es necesario crear un mecanismo de control que actúe sobre los resultados y los factores considerados con el fin de realizar los ajustes correspondientes. En definitiva, el modelo se convierte en una regla de decisión que lo relaciona más directamente con los objetivos.
5- Aplicación:
Finalmente, se pone en práctica la solución obtenida a partir del modelo. Este paso da, pues, por terminado el proceso de decisión.
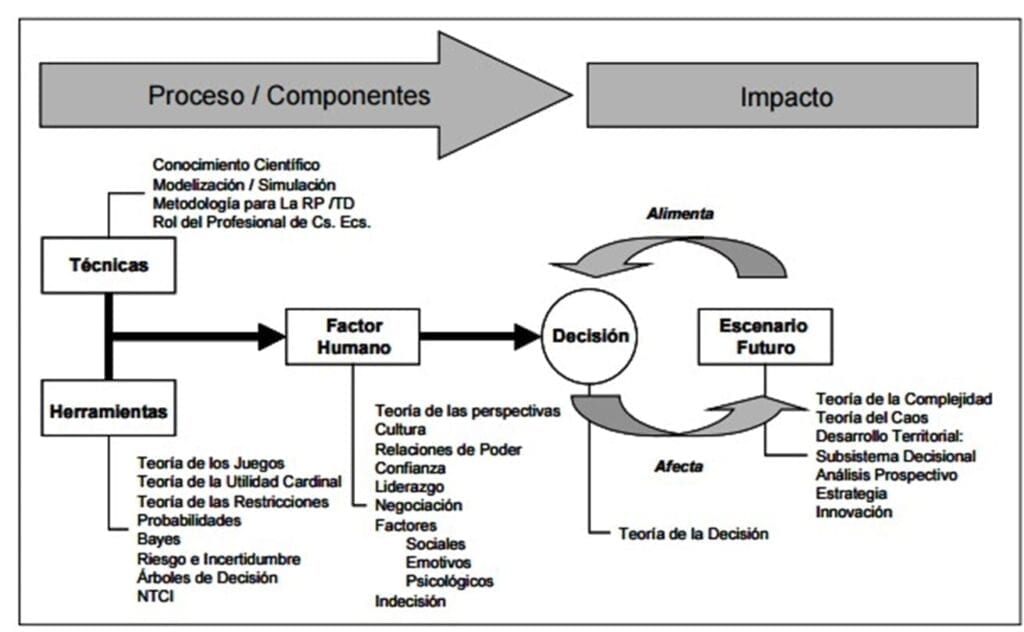
La manera como una persona examina un problema y toma la decisión se puede describir desde diferentes puntos de vista, de acuerdo con los supuestos que la persona realiza. Optimizar un proceso de toma de decisiones implica tener un conocimiento o aproximación a los elementos que la componen, a saber:
- El escenario futuro el cual se puede ver afectado por nuestra decisión y a su vez alimenta a la misma a partir de la comprensión del comportamiento de sus variables
- Las Técnicas y Herramientas de las cuales me puedo valer durante el proceso de Resolución de problemas y toma de decisiones
- Y las condiciones individuales, personales, socio-afectivas y culturales que influyen en aquel que toma la decisión, a la que llamaremos: factor humano. El siguiente modelo esquematiza este proceso.

DESARROLLO DE PENSAMIENTO LÓGICO Y RESOLUCIÓN DE PROBLEMAS
Diversas escuelas han tratado de explicar cómo es que funciona el pensamiento en la solución de problemas. Por ejemplo, encontramos en la psicología cognitiva, históricamente la disciplina que ha provisto de resultados útiles a este propósito, dos enfoques básicos
La teoría del pensamiento asociacionista, que enfatiza como un elemento de una cadena de resolución es asociado con otro y la teoría de la Gestalt, que se sustenta en el entendimiento estructural de la situación a resolver.
De acuerdo al enfoque asociacionista, el proceso de pensamiento se describe como una aplicación de ensayo y error, para hallar la respuesta más plausible a cualquier situación problemática particular, considerando todos los enlaces posibles de asociación a una gran cantidad de posibles respuestas así como las tendencias preexistentes de respuesta. Los elementos explicativos básicos de esta teoría son: el estímulo, una situación de resolución de problema particular, las respuestas, comportamientos particulares para la resolución de problemas y las asociaciones, que se establecen entre un estímulo y una respuesta particulares. Se considera que en la mente se configura una familia de posibles respuestas asociadas con cada situación de problema dada. Además, las respuestas pueden variar pues se jerarquizan de acuerdo a qué tan fuerte es la asociación identificada. Es así que este enfoque enfatiza el aprendizaje por reforzamiento.
De acuerdo con la teoría de la Gestalt, el proceso de resolución de problemas es una búsqueda para relacionar un aspecto de la situación problemática con otro dentro de un entendimiento estructural de tal situación, luego este proceso desarrolla la habilidad para comprender cómo las partes del problema se ajustan conjuntamente para satisfacer los requerimientos del objetivo de solución. El proceso de resolución involucra la reorganización de los elementos del problema en una nueva forma que resulte más legible al que pretende resolver el mismo. El énfasis en el ajuste de los elementos para formar una estructura de análisis (la organización), en la creación de soluciones a nuevas situaciones (pensamiento productivo) y en la reorganización de los elementos del problema (pensamiento creativo); descansa en la idea de que las estructuras u organizaciones mentales son las unidades de pensamiento. Se trata de esta manera de comprender y explicar un proceso mental de tipo creativo de muy alto nivel.
En la lógica dialéctica, la explicación que se da a la dinámica de desarrollo del pensamiento lógico al abordar la resolución de problemas se sustenta en la presencia de dualidades conceptuales, como las que a continuación, se explican.
Concreto – abstracto: Lo concreto y lo abstracto no pueden separarse; son dos aspectos solidarios, dos caracteres inseparables del conocimiento que sin cesar pasan del uno al otro. “Lo concreto verdadero no se encuentra en lo sensible, en lo inmediato. Lo sensible es, en cierto sentido, la primera abstracción. Sensación y percepción separan uno de los aspectos del objeto; su relación con nosotros, el aspecto que nos importa y nos afecta en ese instante”. Penetrar en lo real es alcanzar, por la inteligencia y la razón, conocimientos mediatos que son pensamientos, ideas. Penetrar en lo real es superar lo inmediato para alcanzar “un conjunto cada vez más vasto de relaciones, de detalles, de elementos, de particularidades aprehendidas en un todo”. Este conjunto, ese todo, no puede por otra parte, coincidir con la totalidad de lo real, con el mundo. El acto de pensamiento aísla de la totalidad – por medio de una separación en capas real o “ideal” eso que se llama justamente un “objeto de pensamiento”. Dicho producto “abstracto” del pensamiento no es más misterioso que un producto de la acción práctica. Así, aunque el conocimiento parte de lo concreto, global y “confusamente aprehendido en la percepción sensible”, camina a través del entendimiento de los aspectos y elementos distintos de la situación por medio de puntos de vista abstractos y unilaterales. Por medio de la profundización del contenido y de la investigación racional se dirige hacia la comprensión del conjunto.
Análisis – síntesis: El análisis se esfuerza por penetrar desde afuera, por medio del pensamiento, al objeto. Los seres, lo concreto, se presentan relativamente cerrados ante nosotros, pues cada ser es un todo. Pero esos seres no son absolutamente inaccesibles. El análisis penetra en ellos y los separa, los rompe, sea real o idealmente. El análisis no puede ser nunca exhaustivo pues es infinito; porque lo concreto es mucho más profundo y concreto de lo que se pensaba (considérese el ejemplo del análisis del cuerpo humano donde de los órganos, podemos pasar a las células y de ahí a la química de los átomos). En todo momento el análisis debe tener presente, y aprehender, esa relación compleja, muy frecuentemente contradictoria, de los elementos entre sí y con el todo. Por otra parte, la síntesis se manifiesta como complementaria al análisis. La síntesis se define, en general, como una operación sea experimental (real) o racional (ideal) por medio de la cual se rehace en sentido inverso el camino recorrido por el análisis. La síntesis reconstruye el todo, asegurándose de no omitir nada. Sin embargo la síntesis no se limita a trabajar sobre un cuadro sinóptico creado por el análisis sino que hace que éste mantenga en todo momento el contacto con el todo, por eso mismo guía al análisis, evita que se extravíe.
Inducción – deducción: La inducción va de los hechos a la ley — de un conjunto de hechos particulares a una conclusión general -, sea de manera rigurosa, cuando “la ley resume en una fórmula todos los casos particulares estudiados”, sea amplificante, cuando pasa de un número finito de hechos estudiados, que son necesariamente hechos pasados, a un número infinito de hechos posibles. Para regresar a la aplicación de esta ley a nuevos hechos, es necesaria la deducción. Verdad-error Las verdades científicas no son eternas ni inamovibles, de ser así serían infecundas pues negarían el esfuerzo del pensamiento por pasar de la ignorancia al conocimiento, “de verdades menores a verdades más profundas a través de errores parciales o momentáneos”.Ya que todo error puede ser en sí mismo una verdad parcial o el aspecto de una verdad, permite ampliar los límites de una verdad, negándola inicialmente. Es decir, la verdad se convierte en error antes de ser ampliada
Absoluto-relativo Cada verdad alcanzada es relativa pues “está destinada a superarse, a aparecer bajo aspectos nuevos, a ser superada por leyes y teorías más precisas”, pero en cierto sentido es absoluta, pues el conocimiento científico adquirido posteriormente implica, verifica y complementa al anterior, lo sitúa en su verdad Las verdades “absolutas” se alcanzan a través de los descubrimientos relativos y de los pensamientos individuales, cuyo alcance es limitado. “”La relación de lo absoluto con lo relativo no es otra que la del pensamiento humano con el pensamiento de los individuos” Es esto mismo lo que explica las dualidades: general-particular, modelos genéricos-situaciones específicas.
Teoría-práctica Para comprender lo familiar es preciso superar el entendimiento individual, el punto de vista particular, la práctica inmediata; es preciso pasar a otra escala, a una orden de reflexiones más amplias, teóricas y abstractas en apariencia, sin olvidar ni omitir el hecho de que se trata de uno. Aún las verdades matemáticas son sometidas a discusión por filósofos y matemáticos y se perciben cada vez bajo nuevos aspectos con tal de profundizarlas. lo real, lo concreto, lo humano, lo que se intenta conocer y que habrá que regresar a ello para comprenderlo. Aunque los científicos reconozcan que todo resultado alcanzado con estas reflexiones es ya un conocimiento, buscan de nuevo lo desconocido para profundizar en su verdad. Sin embargo, al ser parte de este mundo que queremos comprender, para conocer los objetos será necesario actuar sobre ellos, sólo así se puede garantizar de alguna manera que el conocimiento adquirido, si bien adquirido es relativo con respecto al lugar que ocupamos en el universo, a la precisión de nuestros instrumentos de medida, a la eficacia de nuestras acciones; será en cierto modo real sea respecto a la idealización que hemos hecho de su naturaleza sea respecto a su estructura que hemos construido de manera subjetiva en nuestro pensamiento.
Macro-micro: Un individuo sólo se comprende verdaderamente si se descubren por una parte sus singularidades y por otra parte sus rasgos más generales, pues se toma conciencia de ellas sólo por medio de éstos. Por otra parte, todo ser inmerso en un conjunto de relaciones sociales es un conjunto de cualidades. Luego, para comprender a un individuo es necesario observarlo de manera alternativa desde el punto de vista social (de sus rasgos generales) y desde el punto de vista privado. “La razón dialéctica aprehende al individuo (singular) pero en la totalidad y por la totalidad” Considerando los conceptos duales que se han presentado, afirmamos que el estudio de las matemáticas enfatiza el desarrollo de capacidades y habilidades intrínsecamente relacionadas con el pensamiento lógico dialéctico. Veamos a continuación cómo es que estos conceptos se ven reflejados en los modelos, particularmente en los modelos matemáticos, de la realidad. (ROSALES, 2005)
MODELOS PARA LA TOMA DE DECISIONES EN LAS ORGANIZACIONES
A continuación, se presenta una serie de modelos mediante los cuales la toma de decisión se puede simplificar, no se busca profundizar en cada una de las disciplinas, sino tener una visión global de las mismas simplificando su explicación con la posible adaptación a la práctica de nuestras organizaciones. Estos modelos son: Maximin o Wald, Maximax, Hurwicz, Laplace y Savage.
Siempre hay que contar con ese umbral probabilístico de incertidumbre por lo que la decisión variará en función de factores externos no controlables pero en la medida de lo posible si evitables y disminuir su impacto lo mas posible para/con la decisión tomada alcanzando el objetivo que se había propuesto.
Se presenta un ejemplo común el cual se irá desarrollando en todos los modelos, usted se encuentra ante una situación de cambio de estrategia de la organización, existen dudas sobre cómo redirigirla y hacer foco en un nuevo nicho de mercado. (RODRIGO, 2012)
Se hace una valoración en función de las variables obtenidas.
| Escenarios | |||
| 1 | 2 | 3 | |
| A | 7 | 8 | 1 |
| B | 10 | 2 | 5 |
| Soluciones C | 5 | 4 | 9 |
1. Modelo Maximin o de Wald
Lo que propone el modelo de Maximin o de Wald es fijar las valoraciones mas bajas dentro de todas las soluciones es decir, las valoraciones mas bajas son 1 para la solución A, 2 para la B y 4 para la C, entonces dentro de este rango se elige C, pues es la mas alta dentro de las peores, la filosofía es la mejor de las peores , esto supone una perdida de información porque no se tienen en cuenta el resto de campos y la opción elegida no podría ser la mas optima.
2. Modelo Maximax
Al contrario que el anterior, el modelo Maximax propone trabajar con los datos que mayor puntuación han obtenido, por ejemplo, en el cuadro las de mayor puntuación son 8 para A, 10 para B y de 9 para C, aplicando la lógica de este modelo se toma como decisión final la B pues su puntuación es superior al resto, la mejor de las mejores, por lo que es la que mas beneficios daría.
3. Modelo de Hurwicz
Este modelo toma una lógica intermedia entre las anteriores, y para el peor valor da un valor de 1-α, mientras que para el valor mas alto otorga un valor de α, donde α es el valor de optimismo que utiliza, este valor oscila de 0 a 1, sin llegar a los extremos para no coincidir con las teorías anteriores, un valor razonable es 1/2, en este caso se trabaja con α=1/4. Por lo que el resultado es el siguiente:
A: 1*3/4 + 8*1/4= 2,75
B: 2*3/4 + 10*1/4= 4
C: 4*3/4 + 9*1/4= 5,25
La opción a elegir en este caso es la C, pues tiene la máxima puntuación.
4. Modelo de razón insuficiente o de Laplace
Laplace plantea la utilización de todos los valores que se han obtenido anteriormente. La lógica que aplica es asignar a cada valor la misma probabilidad (1/n) de tal modo que todos están en igualdad de condiciones. N muestra los posibles estados de la naturaleza, es decir, un ejemplo para esta organización seria: aumento de ganancias, pérdidas o estancamiento.
Con estos criterios la opción sigue siendo la C pues a priori parece la más completa y equilibrada, este método no arriesga en la toma de decisiones.
A: 7*1/3 + 8*1/3 + 1*1/3= 5.3
B: 10*1/3 + 2*1/3 + 5*1/3= 5.6
C: 5*1/3 + 4*1/3+ 9*1/3= 6
5. Modelo de Savage
Se busca la máxima ganancia a través de la pérdida mínima. Entonces para cada una de las soluciones se tienen diferentes resultados, se toman los escenarios (columnas) como referente y dentro de estas se elige el mayor valor para restarlo por cada valor dentro de esa misma columna para cada solución.
Para este ejemplo el valor máximo de la primera columna es 10, por lo que se resta 7,10 y 5 respectivamente, así se realiza en las siguientes columnas. Por lo que la solución C se presenta como la mejor de todas.
| Escenarios | uma | |||
| 1 | 2 | 3 | —– | |
| A | 3 | 0 | 8 | 11 |
| B | 0 | 6 | 4 | 10 |
| Soluciones C | 5 | 4 | 0 | 9 |
HERRAMIENTAS DE MODELACIÓN MATEMÁTICA
Usualmente se afirma que las matemáticas descansan en un número limitado de proposiciones elementales, llamadas axiomas, de las cuales se derivan todas las demás únicamente mediante procesos de inferencia lógica y deducción; sin embargo, las matemáticas requieren de la observación, de la experimentación, de la inducción, de la causalidad; pues surgen de la actividad de la mente humana en un ejercicio continuo de introspección del mundo interior de los pensamientos en relación con el mundo exterior de la realidad; tal relación es de una correspondencia “más o menos como una sombra con el objeto que la proyecta, o como la palma hueca de una mano con el puño cerrado que abraza de la otra.
Existen algunas técnicas matemáticas empleadas para argumentar la toma de decisiones.
INVESTIGACIÓN DE OPERACIONES
La rama de investigación de operaciones (IO) proviene de la administración científica la cual agrego métodos matemáticos como tecnología computacional y una orientación más amplia.
La IO adopta el método científico como estructura para la solución de los problemas con fuerte énfasis en el juicio objetivo.
Las definiciones de la IO varían desde técnicas de las matemáticas específicas hasta el método científico en sí. En general, esas definiciones incluyen tres aspectos básicos comunes al enfoque de la IO a la toma de decisión administrativa.
- Visión sistemática de los problemas que van a ser resueltos
- Uso del método científico en la resolución de problemas
- Utilización de técnicas específicas de estadística, probabilidad y modelos matemáticos para ayudar al que toma las decisiones a solucionar los problemas
La IO enfoca el análisis de operaciones de un sistema y no solamente como un problema particular, la IO utiliza:
- La probabilidad en el enfoque de la IO para decisiones bajo condiciones de riesgo e incertidumbre
- La estadística en sistematización y análisis de datos para obtener solución
- La matemática en la formulación de modelos cuantitativos
La metodología de la investigación de operaciones utiliza seis fases:
- Formular el problema.- Con el análisis del sistema y sus objetivos y las alternativas de acción.
- Construir un modelo matemático para representar el sistema- El modelo expresa el sistema el sistema como un conjunto de variables, de las cuales una por una por lo menos, esta sujeta a control.
- Deducir una solución del modelo.- La solución óptima de un modelo por medio del proceso analítico o del proceso numérico
- Probar el modelo y la solución del modelo.- Construir el modelo que represente la realidad y que debe ser capaz de prever con exactitud el efecto de los cambios en el sistema y la eficiencia general del sistema
- Establecer control sobre la solución.- la solución de un modelo será adecuado mientras las variables incontroladas conserven sus valores y las relaciones entre las variables se mantengan constantes
- Colocar la solución en funcionamiento (implementación). La solución necesita ser probada y transformada en una serie de procesos operacional
Las principales técnicas de la investigación de operaciones Son:
- Teoría de juegos
- Teoría de las colas
- Teoría de los grafos
- Programación lineal.
- Programación dinámica.
- Análisis estadístico y cálculo de probabilidad.
1- Teoría de los juegos
Teoría de los juegos propuesta por los matemáticos Johann Von Neumann propone una formulación matemática para la estrategia y el análisis de los conflictos.
La situación de conflicto ocurre cuando un jugador gana y otro pierde, pues los objetivos en la mira son invisibles, antagónicos e incompatibles entre sí.
La cantidad de Estrategias disponibles es finita y, por lo tanto innumerable. Cada estrategia describe lo que será hecho en cualquier situación.
La teoría de los juegos se aplica cuando:
- La cantidad de participantes es finito
- Cada participante dispone de un número finito de cursos posibles de acción.
- Cada participante conoce los cursos de acción.
- Cada participante conoce los cursos de acción al alcance del adversario, aunque desconozca cuál será el curso de acción escogido por él
- Las dos partes intervienen cada vez y el juego es “suma cero”, es decir puramente competitivos los beneficios de de un jugador son las pérdidas del otro, y viceversa
2.- Teoría de las colas
La teoría de las colas, es la teoría que cuida de los puntos de estrangulamiento y de los tiempos de espera, o sea, de las demoras observadas en algún punto de servicio.
En la teoría de las colas los puntos de interés son: el tiempo de espera de los clientes; la cantidad de clientes en cola; y la razón entre el tiempo de espera y el tiempo de prestación de servicio.
En una situación de cola, existen los siguientes componentes:
- Clientes u operaciones.
- Un pasaje o punto de servicio por donde deben pasar los clientes u operación
- Un proceso de entrada (imputa).
- Una disciplina sobre la cola.
- una organización de servicio.
3.- Teoría de los grafos
La Teoría de los Grafos se basa en redes y diagramas de flechas para varias finalidades. Ofrece técnicas de planeación y programación por redes utilizadas en actividades de construcción y de montaje industrial. Tanto PERT (Programa Evaluación Rebién Technique), como APM (Critical Path Method) son diagramas de flechas que identifican el camino crítico estableciendo una relación directa entre los factores de tiempo y costo, indicando el “óptimo económico” de un proyecto.
El Neopert es una variación simplificada del Pert, posibilitando economía de tiempo en su elaboración.
Las redes o diagramas de flechas se aplican en proyectos que involucran varias operaciones y etapas, varios recursos, diferentes órganos involucrados, plazos y costos mínimos.
Las redes o diagramas de flechas presentan las siguientes ventajas:
- Ejecución del proyecto en el plazo más corto y al menor costo.
- Permiten la interrelación de las etapas y operaciones del proyecto
- Distribución óptima de los recursos disponibles y facilitan su redistribución en caso de modificación
- Provee alternativas para la ejecución del proyecto y facilitan la toma de decisión.
- Identifican tareas u operaciones “críticas” que no ofrecen holgura en el tiempo para su ejecución, y así concentrarse en ellas totalmente.
- Las tareas u operaciones “críticas” afectan el plazo para el término del proyecto global.
- Definen responsabilidad de tornarnos o personas involucradas en el proyecto
4.- Programación lineal
Programación lineal (PL) es una técnica matemática que permite analizar los recursos de producción para maximizar las utilidades y minimizar el costo. Es una técnica de solución de problemas que requiere la definición de los valores de las variables involucradas en la decisión para optimizar un objetivo a ser alcanzado dentro de un conjunto de limitaciones o restricciones, que constituyen las reglas del juego. Tales problemas involucran asignación de recursos, relaciones lineales entre las variables de la decisión, objetivo a alcanzar y restricciones.
El problema de la asignación involucra situaciones como programar la producción para maximizar utilidades, mezclar ingredientes de un producto para minimizar costos, seleccionar una cartera excelente de inversiones, asignar personal de ventas en un territorio o definir una red de transportes intermodales con el menor costo y mayor rapidez.
La Programación lineal presenta características como:
- Busca la posición óptima de relación con un objetivo. La finalidad es minimizar costos y maximizar beneficios en función del objetivo preestablecido.
- Supone la elección entre alternativas o combinación de esas alternativas
- Considera límites o restricciones que cercan la decisión.
- Las variables deben ser cuantificables y tener relaciones lineales entre sí.
5.- Programación dinámica
La programación dinámica se aplica en problemas que poseen varias etapas interrelacionadas, donde una decisión adecuada a cada una de las etapas debe adoptarse, sin perder de vista el objetivo final. Únicamente cuando el efecto de cada decisión se evalúa es que se efectúa la elección final.
6.- Probabilidad y análisis estadístico
El análisis estadístico es el método matemático utilizado para obtener la misma información con la menor cantidad de datos. Una de sus aplicaciones más conocidas es el control estadístico de calidad (CEQ) en el área de producción. Los métodos estadísticos permiten producir el máximo de información a partir de los datos disponibles.
La aplicación de la estadística a los problemas de calidad comenzó con Malter A. Shewhart en el transcurso de la Segunda Guerra Mundial.
a.- Control estadístico de calidad
La idea inicial era aplicar metodología estadística en la inspección de calidad y llegando a la calidad asegurada con la finalidad de obtener conformidad con las especificaciones y proporcionar alto grado de confiabilidad, durabilidad y desempeño en lo productos.
El control estadístico de la calidad se base en técnicas de determinación del momento en que los errores tolerados en la producción empiezan a rebasar los límites de tolerancia, es cuando la acción correctiva se hace necesaria.
El control estadístico de la calidad tiene por objetivo localizar desviaciones, errores, defectos o fallas en el proceso productivo, comparando el desempeño con el estándar establecido. Esa comparación puede realizarse de res formas:
- Control de calidad 100%.Corresponde a la inspección total de la calidad. El control de calidad (QC) total hace parte del proceso productivo y se inspeccionan todos los productos
- Control de calidad por muestreo Es el que se hace por lotes de muestras recogidos para su inspección. El control de muestras sustituye el control total ya que no interfiere en el proceso productivo. Si se aprueba la muestra todo el lote se aprueba. Se rechaza la muestra, se deberá inspeccionar todo el lote.
- Control de calidad aleator Es el QC probabilística y consisten en inspeccionar solamente un cierto porcentaje de productos o del trabajo en forma aleatoria.
b.- Calidad total
J. M. Juran (nació en 1904). Extendió los conceptos de calidad para toda la empresa con su control total de la calidad.
Mientras el control estadístico de la calidad se aplica apenas en el nivel operacional, y de preferencia en el área de producción y manufactura, la calidad total extiende el concepto de calidad a toda la organización, desde el nivel operacional hasta el institucional, abarcando todo el personal de la oficina y de la base de la fábrica en un todo.
Las ventajas son:
- Reducción de desperdicios
- Disminución de los ciclos de tiempo y de los tiempos de resultados
- Mejoría de la calidad de los resultados (productos o servicios).
Ambos constituyen enfoques de incremento para así excelencia en la calida de los productos y procesos, además de proporcionar una formidable reducción de costos.
SIX-SIGMA
Sigma es una medida de variación estadística. Cuando se aplica a un proceso organizacional, se refiere a la frecuencia con que determinada operación o transacción, utiliza más que los recursos mínimos para satisfacer al cliente.
El programa 6-sigma utiliza varias técnicas en un método proceso paso a paso para alcanzar metas bien definidas. La principal diferencia es que con el 6-sigma ya que no se busca calidad por calidad, pero se pretende perfeccionar todos los procesos de una organización. En la práctica, el 6-sigma se diferencia de la calidad total en cuatro áreas básicas:
- Mayor amplitud de la aplicación. se aplica dentro del área del producto y manufactura y no en el proyecto, finanzas, etcétera. El 6-sigma es para toda la organización.
- Estructura de implementación más senc Los cinta negra se dedican íntegramente a los cambio y quedan fuera del cotidiano. La administración premia o castiga por la mejora de los negocios.
- Herramientas más profund 6-sigma se profundiza para describir la situación actual y prever el futuro. Existe una fuerte dosis de estadística aplicada y una mejor comprensión de cómo los procesos se comportan, un software para auxiliar y un mapa para la aplicación de las herramientas. De aplicación de herramientas permite aclarar los problemas y mejorar.
- Fuerte vinculación con la saluda (financiera) de los negoc El 6-sigma aborda los objetivos de la empresa y se certifica de que todas las áreas clave para la salud futura de la empresa contienen medidas cuantificables con meas de mejor y planos y aplicación detallados.
El 6-sigma busca la eficacia organizacional en tres dimensiones que deben funcionar conjuntamente:
- Reducción del desperdicio. A través del concepto de emprendimiento exacto, sin excedentes, sólo lo esencial, o esfuerzo de tiempo futuro, o reducción del ciclo de tiempo o incluso eliminación de lo que no tiene valor para el cliente, imprimiendo la velocidad a la empresa.
- Reducción de los defecto Es el 6-sigma propiamente,
- Involucramiento de las person A través de la llamada “arquitectura humana”.
BALANCE SCORE CARD (BSC)
Las medidas e indicadores afectan significativamente la conducta de las personas en las organizaciones. (FUENTES, 2008)
Lo que una organización define como indicador es lo que se obtendrá como resultados. El punto central de los sistemas y medidas tradicionalmente utilizados en las organizaciones se concentra puramente en aspectos financieros o cuantitativos, e intenta controlar comportamientos.
Es un método de administración enfocado en el equilibrio organizacional y se basa en cuatro perspectivas básicas, que son las siguientes:
- Finanzas. Analiza el negocio desde el punto de vista financiero. Este punto involucra los indicadores y medidas financieras y contables que permiten evaluar la conducta de la organización frente a puntos como utilidad, retorno sobre inversiones, valor agregado al patrimonio y otros indicadores que la organización adopte como relevantes para su negocio.
- Client Analiza el negocio desde el punto de vista de los clientes. Incluye indicadores y medidas como satisfacción, participación en el mercado, tendencias, retención de clientes y adquisición de clientes potenciales, así como valor agregado a los productos/servicios, posición en el mercado, nivel de servicios agregados a la comunidad por los cuales los clientes contribuyen indirectamente, etcétera.
- Procesos internos Analiza el negocio desde el punto de vista interno de la organización. Incluye indicadores que garantizan la calidad intrínseca a los productos y procesos, la innovación, la creatividad, la capacidad reproducción y la optimización con las demandas, la logística y la optimización de los flujos, así como la calidad de la información, de la comunicación interna y de las interfaces.
- Aprendizaje/crecimiento organización Analiza el negocio del punto de vista de aquello que es básico para alcanzar el futuro con éxito.
TÉCNICA MONTECARLO
Es un método simplificado de simulación, pero también incluye factores de probabilidad. La simulación es guiada por un muestreo al azar para tomar en cuenta la probabilidad de que el evento suceda.
El muestreo al azar se usa para simular sucesos naturales con el fin de determinar la probabilidad de los eventos bajo estudio.
Se emplea una tabla de números al azar para obtener la muestra al azar. El Montecarlo es un medio de tanteo para ver que sucedería cuando ciertos eventos, normales y anormales, se presentan.
Este enfoque es productivo y dice lo que probablemente sucederá en los eventos reales sin analizar los eventos comprobables existentes. Las aplicaciones posibles son muy numerosas.
Pueden usarse para resolver problemas con estas preguntas típicas:
- ¿Cuál es la probabilidad de un evento o combinación de eventos, que ocurran en un proceso dado?
- ¿Qué decisión debe tomarse en base a las alternativas posibles?
LÍNEAS DE ESPERA ( FILAS )
Se presentan problemas administrativos debido a:
- Se hace esperar a empleados, máquinas o materiales debido a instalaciones insuficientes para manejarlos de inmediato.
- Ocurre la utilización de las instalaciones a menos del máximo a causa de la secuencia de la llegada de recursos que emplean las instalacion
Hay pérdidas de tiempo, mano de obra no utilizada y costos excesivos causados por las líneas de espera o filas. Minimizar estas pérdidas es el objetivo de esta técnica.
Las filas están relacionadas con el flujo; Ejemplo: el material que espera ser procesado por una máquina, los aviones que dan círculos sobre un aeropuerto en espera de instrucciones, incluyen el flujo de la combinación y de los materiales. (BARRERA, 2006)
CONCLUSIÓN
En la vida diaria tomamos un sinfín de decisiones, a veces evadimos el camino largo y nos inclinamos por decisiones cuantitativas basadas en sentimientos y emociones, quizás por ignorancia de métodos de modelación matemática, no obstante, este no debe de ser un impedimento, no debemos cerrarnos a la posibilidad de su uso, aunque esto represente una investigación ardua del tema y una capacitación.
Existen algunas decisiones “simples” en las que influyen múltiples factores e indicadores emocionales, en estos casos la modelación resultaría compleja, pero siempre se debe de tomar en cuenta que el análisis y la lógica matemática sirve para reducir riesgos al obtener resultados cuantificables.
AGRADECIMIENTOS
Agradecida con Dios por todas sus bendiciones, igualmente por la oportunidad de trabajar en el proceso de mejorarme a misma.
A mi “alma mater” el Instituto Tecnológico de Orizaba por su esmero en la formación de profesionistas de calidad, a mi Profesor M.A.E Fernando Aguirre y Hernández por su dedicación, esmero y compromiso al compartir sus conocimientos.
¡A Dios por la vida y por la ciencia!
PROPUESTA DE TESIS
IMPLEMENTACIÓN DE SIX SIGMA EN EL AREA DE INSPECCIÓN EN EMBOTELLADORA TROPICAL ORIZABA, VER.
Objetivo: Mediante six sigma reducir el número de defectos por millón en el área de inspección, de planta Pepsi Orizaba.
BIBLIOGRAFIA
- BARRERA, M. E. (2006). Obtenido de GESTIOPOLIS: https://www.gestiopolis.com/tecnicas-para-la-toma-de-decisiones/
- BOREA, F. (2002). CIENCIARED. Obtenido de http://www.cienciared.com.ar/ra/usr/4/26/m0.pdf
- DAROS, L. C. (s.f.). UNIVERSIDAD DE VALENCIA.Obtenido de: https://riunet.upv.es/bitstream/handle/10251/16502/TomaDecisiones.pdf
- D (s.f.). DEFINICIÓN.DE. Obtenido de http://definicion.de/pensamiento-logico/
- FUENTES, S. T. (2008). GESTIOPOLIS. Obtenido de: https://www.gestiopolis.com/teoria-matematica-administracion-investigacion-operaciones/
- MACHADO, D. U. (2016). Obtenido de GESTIOPOLIS: https://www.gestiopolis.com/modelos-economico-matematicos-la-decision-empresarial/
- RODRIGO, G. (2012). PDCAHOME. Obtenido de: https://www.pdcahome.com/4655/modelos-para-la-toma-de-decisiones/
- VALDIVIA, F. A. (2013). SCRIBD. Obtenido de: https://es.scribd.com/doc/225097600/Concepto-de-Modelacion-Matematica