En el presente documento se aborda el tema de lógica difusa, comenzando por una breve exposición de antecedentes de este concepto por parte de su autor Lofti Zaedeh, posteriormente se aborda los principios para analizar cada uno de las etapas que llevan a la generación de estos sistemas, incluyendo en este aspecto conceptos tales como: incertidumbre y probabilidad, marcando las principales diferencias entre ambas. Por último se expone su aplicación en el área de la administración organizacional.
Palabras clave: lógica difusa, incertidumbre, sistemas.
Introducción
La oportunidad que genera la lógica difusa es poder formalizar el pensamiento lógico dialéctico, aplicando matemáticas, esto gracias a la unión de la tradición clásica aristotélica, seguida y transformada por las matemáticas con la lógica dieléctrica. La matemática difusa, ya como herramienta de cálculo de criterios de verdad, inicia de una escala de valores desde el más falso a la más verdadero, generando un resultado cuantitativo, lo que resulta en garantizar la opción más cerca a la verdad. La teoría de la lógica difusa proporciona a través de las matemáticas, poder modelar la incertidumbre de los procesos cognitivos de las personas.
Antecedentes
El término de lógica difusa fue generado en los años setenta por Lofti Zaedeh. Posteriormente en 1974 Ebrahim Mamdani aplica los conceptos de lógica difusa en el control de procesos y crea el primer control difuso para regular un motor de vapor. En 1985 Takagi y Sugeno establecen la teoría del control difuso. Sus aplicaciones en control de procesos se evidencian en la industria, medicina, aeronáutica y electrónica. (Robaina, 2010)
Principios de lógica difusa
La lógica difusa o Fussy logic por su nombre en inglés, está orientada a la modelización de modos de razonamientos imprecisos, que son importantes para el trazo hacia la toma de decisiones racionales en un ambiente de incertidumbre e imprecisión. Esto depende de la habilidad de inferir una respuesta cercana a preguntas que se basan en un conjunto de conocimientos que son inexactos, incompletos o no del todo confiables. La lógica difusa permite representar el conocimiento común del tipo lingüístico cualitativo en un lenguaje matemático a través de la teoría de conjuntos difusos. (Pérez, 2007)
La lógica difusa tiene el propósito de identificar los resultados de un fenómeno no lineal sin dejar a un lado las circunstancias en las que da y las características cualitativas; por otro lado las estadísticas tradicionales y matemática lineal solo dan una aproximación puntual o funcional de su comportamiento y de un fenómeno en general. (Mendoza, 2009)
La lógica difusa se fundamenta en conceptos que son percibidos de manera diferente por cada persona. Por ejemplo hay personas que conceptualizan una persona delgada si pesa menos de 70 kg. Otras dependiendo de su punto de vista las conciben en estado de gordura con un peso arriba de 70 kg. Es por esto que los conjuntos delgado, gordo y obeso son llamados conjuntos difusos. Un conjunto difuso es un conjunto con límites borrosos o no del todo bien establecidos. Posteriormente una vez clasificadas las variables en los conjuntos difusos, se les asigna un valor, estos valores tiene que ver con el contexto en el que se encuentre el problema. En la lógica difusa se le asigna un porcentaje de pertenencia a un conjunto que esta numéricamente del mismo. Este concepto es llamado grado de membresía, que puede tomar valores de 0 a 1; el número 1, representa pertenencia al conjunto y 0 ninguna pertenencia al conjunto.
Esto se puede ejemplificar en la siguiente tabla.
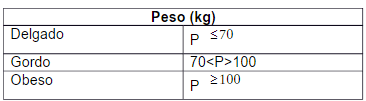
Lógica Difusa
Tabla 1. Elaboración propia
Se definen los nuevos intervalos de los conjuntos difusos, la cual es llamada función membresía (µ). La forma de los intervalos se elige tomando en cuenta la experiencia de las personas, sobre el concepto de estado físico en kilos. A esta traducción de los valores del mundo real a lógica difusa a través de funciones de membresía, se le llama fussyficación.
Se realiza un gráfico en donde el eje “y” es el grado de membresía, que describe cuantitativamente la función de membresía. En el eje de las “x” se establece los kilos. El nombre asociado (delgado, gordo, obeso) es llamado significación lingüística y describe cualitativamente la función de membresía. La forma de la función de membresía es elegido de acuerdo a la situación problemática que se resolverá. Hay formas diferentes por ejemplo: triangular, gaussiana, trapezoidal, sigmoidal, entre otras. El grado de membresía asociado dependiendo de la función de membresía, es nombrado grado de pertenencia (GP).
A partir de las funciones de membresía se pueden tomar una decisión, a este paso se le conoce como inferencia. De acuerdo a la experiencia o percepción que se presenten en el problema, a esto se le conoce como reglas difusas y pueden ser escritas de la forma si…… entonces.
A partir de la función de membresía de entrada y de salida se continua con la siguiente metodología:
- Proceso de inferencia. Para cada grado de pertenencia asociados a la variable en medición se generan conclusiones. Esto puede ser por el método de truncamiento, que consiste en cortar la función de membresía de salida, para que los valores mayores al grado de pertenencia asociado desaparezcan. O por el método de escalamiento, el cual consiste en escalar la función de membresía en proporción con el grado de pertenencia.
- Se realiza una conclusión final combinando las conclusiones difusas.
- Por último la conclusión final se defuzzyfica, esto es se lleva nuevamente al mundo real, a través del uso de diversas técnicas como:
- Promedios de máximos, el cual calcula el promedio de todas las variables que tienen el mayor grado de membresía.
- Método de centro. El cual calcula el promedio ponderado de la salida.
Para la selección del método de deffuzyficacion, será de acuerdo al que cumpa las necesidades y comportamiento del proceso. A pesar que los conceptos de lógica difusa surgen de la experiencia de la situación en problema su campo de aplicación ha sido importante en procesos en donde es difícil predecir o modelar matemáticamente. (Guzmán, 2006)
Lógica difusa y probabilidad
La probabilidad representa datos sobre la frecuencia de ocurrencias de un suceso bien definido sobre el número total de eventos posibles. Por otro lado el grado de pertenencia difuso representa las similitudes de un evento con respecto a otro evento, en el que las características de esos eventos no están bien definidas.
Incertidumbre
Se puede clasificar a la incertidumbre en: determinista, aleatoria, ambigua o no especifica, vaguedad y confusión. (Torres & Tranchita, 2004) A continuación se detallan cada una de ellas:
Determinismo. Es el conocimiento perfecto de los resultados y de la ocurrencia de los eventos, desde este punto no es considerada la incertidumbre.
Incertidumbre aleatoria. Esta ocurre cuando los posibles eventos resultantes de un experimento son conocidos, por ejemplo el lanzar una moneda.
Incertidumbre de ambigüedad o no específica. Esto es cuando una afirmación que puede ser verdadera o falsa. En este aspecto la probabilidad se establece de forma empírica, subjetiva o experimental y puede darse en términos de rangos en lugar de valores absolutos. En este punto los eventos no están especificados o bien definidos, ya que hay carencia de información. Esto es la vaguedad imposibilita establecer la verdad o falsedad de una situación.
Incertidumbre de confusión. Este tipo presenta características tanto ambiguas como vagas.
Si la incertidumbre es de tipo aleatorio, desde el aspecto de probabilidad, puede ser modelado los problemas de incertidumbre asignando probabilidades a los distintos sucesos por medio de la frecuencia relativa y el análisis estadístico. Así podemos obtener una medición adecuada de la probabilidad de que los eventos sucedan.
Pero hay situaciones en que esto no es posible desde el punto de vista subjetivo, ya que la probabilidad se considera como una medida personal de la incertidumbre o de creencia sobre un evento o un objeto y la probabilidad no existe, ya que no está definido. Es por esto que algunos problemas pueden ser modelados, debido a que no se tienen datos estáticos, pero su probabilidad puede ser asignada con base en la creencia de las personas sobre la ocurrencia. Entre las técnicas para el modelaje de la incertidumbre están las redes Bayesianas y las cadenas de Markow.
Para el caso de ambigüedad y la vaguedad, en donde no es posible definir de manera precisa la verdad o falsedad de una afirmación, el modelaje de la incertidumbre se realiza por lógica difusa.
Sistemas de lógica difusa
Un sistema de lógica difusa emplea la inferencia, el cua está compuesto por cinco bloques, como se visualiza en la figura no. 1. Una base de reglas que contienen cierto número de reglas difusas sí…. Entonces…, una base de datos que define las funciones de pertenencia de los conjuntos difusos usados en las reglas difusas, una unidad de toma de decisiones en la que se determinan las operaciones de inferencia de acuerdo a las reglas, una interfaz de difusión en la que se trasforma las entradas especificas en grados de equivalencia con valores lingüísticos y una interfaz de defusificación que convierte los resultados difusos de la inferencia en una salida precisa.
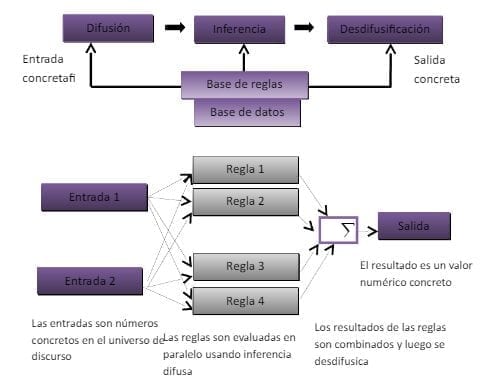
Sistema de lógica difusa. (Torres & Tranchita, 2004)
Hay dos tipos de modelos difusos de diferenciación se basa en la consecuente de las reglas. El primer modelo es el sistema de tipo Mamdani. En este los consecuentes de las reglas son funciones de pertenencia posteriormente estas regla son evaluadas, por un operados de agregación que es una función máximo, por lo que se obtiene un conjunto difuso que luego es desdifusificado.
El otro modelo es el tipo Tsukamoto, en el los consecuentes de la regla son funciones monótonamente no-decrecientes. La salida inferida década regla se reduce como un valor cierto inducido. La salida globales el promedio ponderado de la salida de cada regla.
En los dos sistemas el consecuente de cada regla es una entrada más un término constante, y la salida final es el promedio ponderado de la salida de cada regla. (Torres & Tranchita, 2004)
Lógica difusa en la administración
Los modelos clásicos de racionalidad en el área de toma de decisiones, como lo son la teoría normativa de la decisión, métodos descriptivos y la teoría de juegos son hoy en día la base de los sistemas de ayuda de la decisión y soportan a la administración moderna, pero estos modelos dejan a un lado la subjetividad humana. La administración lógica utiliza modelos difusos integrados para la toma de decisiones y tiene miras a logra coherencia organizacional, la toma de decisiones organizacionales puede estar enfocada de diferentes puntos, ya sea la psicología, economía y la administración. Para los dos primeros se ha utilizado modelos matemáticos en la llamada psicología y economía experimental, emplean modelos de racionalidad limitada, que tratan de describir como el ser humano decide. Otro aspecto en la toma de decisiones es por medio de sistemas expertos, a través de la inteligencia artificial, con la programación de incertidumbre. (Keropyan & Gil-Lafuente, 2011)
Por otro lado la administración lógica emplea modelos basados en lógica difusa por medio de técnicas de ingeniería del conocimiento, a partir de la literatura y la experiencia, para encaminar a la organización hacia la competitividad. Se clasifican tres modelos:
- Modelo cognitivo. Emplean el uso de lógicas multivalentes y otros elementos de lógica difusa tales como los modificadores para transformar en modelos formales el conocimiento de los expertos y la información de respaldo.
- Modelos estructurales. Emplean relaciones difusas para tener en consideración la complejidad estructural de organizaciones y su encajamiento n el entorno.
- Modelo de cálculo en la incertidumbre. Emplea la aritmética difusa, para visualizar en los cálculos de las variables dependientes, las variaciones posibles de las variables dependientes. (Espín & Vanti, 2006)
Conclusión
La lógica difusa o también llamada lógica borrosa, es la lógica que emplea expresiones inciertas o imprecisas, este análisis se realiza mediante la combinación de variables de entrada, que están definida en términos de conjuntos difusos, a través de grupos de reglas que generan uno o varios valores de salida. Una de las aplicaciones con respecto a la administración es poder tomar decisiones estratégicas para la organización, considerando en primera instancia cuestiones objetivas y no dejando a un lado características subjetivas que influyen, en el resultado de las decisiones.
Tema de tesis
Propuesta de un modelo de lógica difusa para la cuantificación de la satisfacción del cliente, en el servicio de post venta en una agencia de autos.
Objetivos
Diseñar una encuesta, para obtener la información correspondiente al grado de satisfacción por parte de los clientes de la agencia de autos. Definir las variables para realizar el conjunto difuso, en base las respuestas obtenidas en la encuesta.
Referencias
- Espín, R., & Vanti, A. (2006). Administración lógica: un estudio de caso en una empresa de comercio exterior. revista de administracao e contabilidade da Unisinos, 2(2), 69-77.
- Guzmán, V. (2006). La lógica difusa en ingeniería: principios, aplicaciones y futuro. Ciencia y Tecnología, 24(2), 87-107.
- Hassan, S., Mata, M., & Garmendia, L. (s.f.). Aplicación de lógica difusa a sistemas sociales con agentes software. Matematicas en las ciencias de la computacion.
- Keropyan, A., & Gil-Lafuente, A. M. (2011). A fuzzy-based decision model application on strategic management. African Journal of Business Management, 5(15), 6586-6590.
- Mendoza, L. (2009). Sistema de lógica difusa. una aplicación a la percepción empresarial. Universidad & Empresa, 17, 252-270.
- Pérez, I. (2007). Lógica difusa para principiantes: teoría y práctica. Caracas, Venezuela: UCAB.
- Robaina, D. (2010). Lógica difusa aplicada a la toma de decisiones. Industrial, 31(2), 2-5.
- Torres, A., & Tranchita, C. (2004). ¿Inferencia y razonamiento probabilístico o difuso? Facultad de ingeniería, 157-165.


