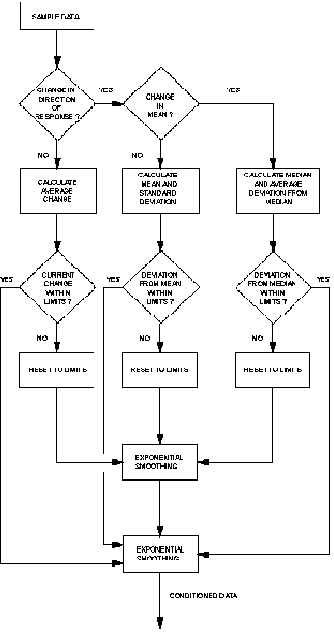
¿Qué es proceso estadístico?
- El proceso estadístico está parado para el control de proceso estadístico.
- El proceso estadístico no refiere a una técnica, a un algoritmo o a un procedimiento particular.
- El proceso estadístico es una filosofía de la optimización referida a mejoras de proceso continuas, usando una colección de las herramientas (estadísticas) para:
a- datos y análisis del proceso
b- fabricación de inferencias sobre comportamiento de proceso
c- toma de decisión.
- El proceso estadístico es un componente dominante de las iniciativas totales de la calidad.
- En última instancia, búsquedas del proceso estadístico para maximizar beneficio cerca.
- mejorar calidad del producto
- mejorar productividad
- aerodinamizar proceso
- Reducción de despilfarro
- Reducción de emisiones
- mejorar servicio de cliente, etc.
Herramientas para el proceso estadístico
Las herramientas comúnmente usadas en el proceso estadístico incluyen
- Organigramas
- Gráficas de funcionamiento
- Gráfica y análisis de pareto
- Diagramas de causa-efecto
- Histogramas de la frecuencia
- Gráficas de Control
- Estudios de la capacidad de proceso
- Planes de muestreo de aceptación
- Diagramas de dispersión
- Cada herramienta es simple poner en ejecución
- Estas herramientas se utilizan generalmente para complementarse, más bien que se emplean como técnicas independientes
Organigramas
- No tenga ninguna base estadística
- son las herramientas excelentes de la visualización
- Demostración de los organigramas
- El progreso del trabajo
- El flujo del material o de la información con una secuencia de operaciones
- Los organigramas son útiles en un análisis de proceso inicial
- Los organigramas se deben complementar por los organigramas de proceso o los organigramas de proceso (detallados) si están disponibles
- Cada uno implicado en el proyecto debe dibujar un organigrama del proceso que es estudiado para revelar las diversas opiniones de cómo el proceso funciona.
Organigrama del ejemplo de un procedimiento para asegurar calidad de los datos.
Las Gráficas de funcionamiento
Las gráficas de funcionamiento son simplemente diagramas de características de proceso contra tiempo o en secuencia cronológica. No tienen base estadística, sino son útiles en revelar
- Tendencias
- Relaciones entre las variables
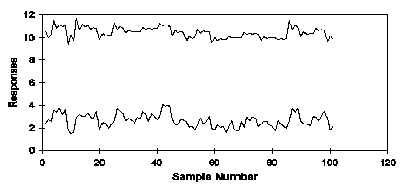
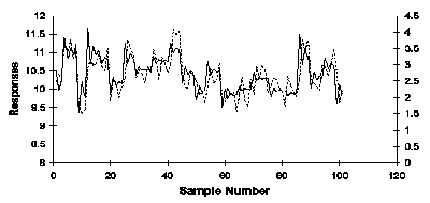
Las gráficas de funcionamiento se pueden utilizar para estudiar relaciones entre las variables. Por ejemplo, en la carta antedicha, la relación entre las 2 variables es difícil de discernir. Para facilitar esto, los escalamientos apropiados para los diagramas deben ser elegidos. Si cada uno trazó la variable tiene su propia escala del y-axis, la gráfica de funcionamiento antedicha entonces se convierte,
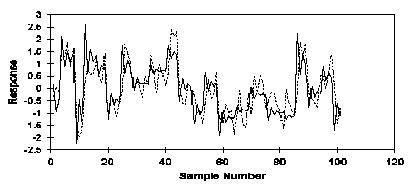
Ahora, la relación entre los dos se convierte en mucho clarificante. Este método fallará obviamente cuando hay más de dos variables. Sin embargo, si las variables se estandarizan antes de trazar, sólo un solo eje común es necesario, y los resultados son justos tan claramente como los anteriores.
Vilfredo Pareto (1848-1923) descubrió eso:
- El 80% de la abundancia en Italia fueron llevados a cabo por el 20% de la población;
- El 20% de clientes consideraron el 80% de ventas;
- El 20% de piezas consideraron el 80% coste, etc.
- Estas observaciones fueron confirmadas por Juran (1960) y dadas lugar a qué se conoce como el principio de Pareto .
El principio de Pareto indica eso:
» no todas las causas de un fenómeno particular ocurren con la misma frecuencia o con el mismo impacto »
Tales características se pueden destacar usando las Gráficas de Pareto
Cartas y análisis de Pareto
- Las gráficas de Pareto demuestran los factores con la más frecuencia posible que ocurren
- El análisis de las gráficas de Pareto ayuda a hacer el mejor uso de recursos limitados apuntando los problemas más importantes para abordar
Por ejemplo:
- Los productos pueden sufrir de diversos defectos, pero
- Los defectos ocurren en diversa frecuencia
- Solamente algunos explican la mayoría de los defectos presentes
- Diversos defectos incurren en diversos costes
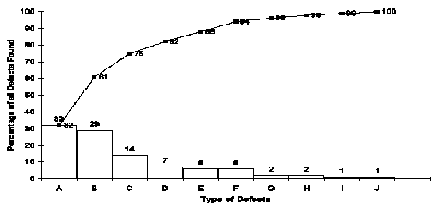
Una línea de productos puede experimentar tan una gama de los defectos (A, B, C…
J). Trazando la contribución del porcentaje de cada tipo para sumar el número de averías, da barra-traza en el diagrama siguiente. Después si, cada uno de estas contribuciones se suma secuencialmente, se obtiene un diagrama de línea acumulativa Estos dos diagramas juntos hacen para arriba la gráfica de Pareto.
Ejemplo de la carta de Pareto
De la información sobre la gráfica, el fabricante podría por ejemplo,
- concéntrese en la reducción de los defectos A, B y C puesto que hacen para arriba el 75% de todos los defectos
- céntrese en la eliminación del defecto E, si el defecto E causa el 40% de pérdida monetaria
Los diagramas del Causar-y-efecto:
También se llaman:
- Diagramas de Ishikawa ( Dr. Kaoru Ishikawa, 1943)
- Diagramas del fishbone
- Los diagramas de causa – efecto no tienen una base estadística, sino son ayudas excelentes para solucionar de problema y el trouble-shooting
- Los diagramas del Causar-y-efecto pueden
- revelar las relaciones importantes entre varias variables y causas posibles
- proporcionar la penetración adicional en comportamiento de proceso
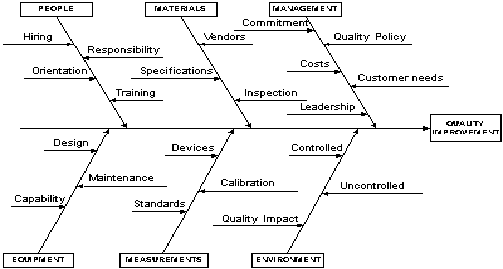
Ejemplo de un diagrama del Causa-efecto
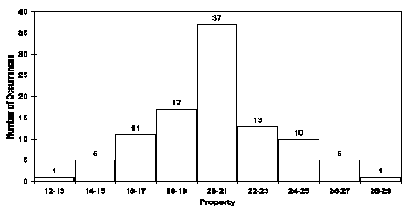
Histograma de la frecuencia
El histograma de la frecuencia es un método gráfico y fácilmente interpretado muy eficaz para resumir datos El histograma de la frecuencia es una herramienta estadística fundamental del proceso estadístico
Proporciona la información alrededor:
- El promedio (medio) de los datos
- La variación presente en los datos
- El patrón de la variación
Si el proceso está dentro de lo especificado
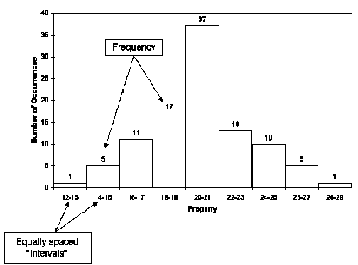
Histogramas De Dibujo De la Frecuencia
En histogramas de dibujo de la frecuencia, considere las reglas siguientes:
- Los intervalos deben ser espaciados igualmente
- Seleccione los intervalos para tener valores convenientes
- El número de intervalos está generalmente entre 6 a 20
- Las cantidades pequeñas de datos requieren pocos intervalos
- 10 intervalos son suficientes para 50 a 200 lecturas
Procesos que no están en un estado del control estadístico:
- demuestra las variaciones excesivas
- exhiba las variaciones que cambian con tiempo
Gráficas de Control
Se utilizan para detectar si un proceso es estadístico estable . Las gráficas del control distinguen entre las variaciones
- Eso espera normalmente de las causas debidas de proceso de la ocasión o del campo común
- Ese en un cierto plazo el cambio debido a las causas asignables o especiales
Variaciones debido a las causas comunes
- tenga efecto pequeño en el proceso
- sea inherente al proceso debido a:
- La naturaleza del sistema
- Se maneja la manera el sistema
- Se organiza y se funciona la manera el proceso
- La lata solamente se quite cerca
- Fabricación de modificaciones al proceso
- cambiar el proceso
- es la responsabilidad de una gerencia más alta
Calas variaciones debido a las causas especiales son :
- localizado en naturaleza
- Excepciones al sistema
- Anormalidades consideradas
- A menudo específico a :
- Cierto operador
- Cierta máquina
- Cierta hornada del material, del etc.
- La investigación y el retiro de las variaciones debido a las causas especiales son dominantes a la mejora de proceso.
Nota : A veces la delineación entre las causas comunes y especiales puede no estar muy clara
Los principios detrás del uso de las gráficas de control son muy simples y se basan en el uso combinado de
- Gráficas de funcionamiento
- Prueba de la hipótesis
El procedimiento es :
- Muestree el proceso en los intervalos regulares
- trace la estadística (o una cierta medida del funcionamiento), e.g.
- Medio
- Gama
- Variable
- Número de defectos, del etc.
- compruebe (gráficamente) si el proceso está bajo control estadístico
- Si el proceso no está bajo control estadístico, haga algo sobre él
Diversas gráficas se utilizan dependiendo de la naturaleza de las cartas comúnmente usadas planeadas de los datos son:
- Para los datos continuos (de las variables):
- Medio de la muestra de Shewhart (c- gráfica)
- Gama de la muestra de Shewhart ( R – gráfica)
- Muestra de Shewhart ( X – gráfica)
- Suma acumulativa (CUSUM)
- Gráfica exponencial cargada del promedio móvil (EWMA)
- Gráficas Mover-medias y de la gama
- Para ( cualidades y contable) los datos descritos :
- Proporción de la muestra defectuosa ( p – gráfica)
- Número de la muestra de los defectives ( np – gráfica)
- Número de la muestra de los defectos ( c – gráfica)
- Número de la muestra de defectos por la unidad ( u – gráfica s – gráfica)
Calas gráficas de control hacen asunciones sobre la estadística trazada, a saber
- es independiente , es decir. Un valor no es influenciado por su último valor y no afectará los valores futuros
- Se distribuye normalmente, es decir los datos tienen una función normal de la densidad de la probabilidad
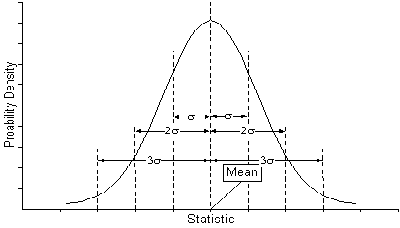
Función Normal De la Densidad De la Probabilidad
Las asunciones de la normalidad y de la independencia permiten a predicciones ser hechas sobre los datos.
La distribución normal N ( m, s 2) tiene varias características distintas:
- La distribución normal es acampanada y es simétrica
- El medio, m , está situado en el centro
- Las probabilidades que un punto, x, mentiras cierta distancia más allá del medio es:
- Banda (x > m + 1,96 s) = banda ( x > m – 1,96s) = 0,025
- Banda (x > m + 3,09 s) = banda ( x > m 3,09s) = 0,001
S es la desviación de estándar de los datos
Gráficas de control: interpretación
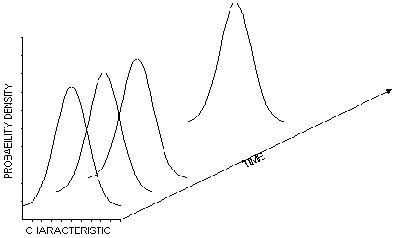
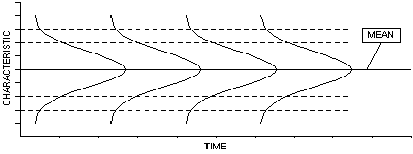
- Las gráficas del control son distribuciones normales con una dimensión agregada del tiempo.
- Las gráficas del control son cartas de funcionamiento con distribuciones normales sobrepuestas
Car
Gráficos para probar hipótesis
Las gráficas del control proporcionan los medios gráficos para probar hipótesis sobre los datos que son supervisados.
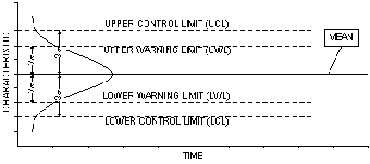
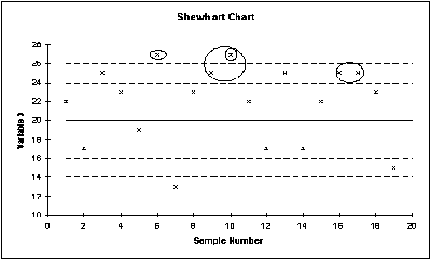
Considere la gráfica comúnmente usada de Shewhart como ejemplo.
La gráfica X de Shewhart con límites del control y de la advertencia
La probabilidad de una muestra que tiene un valor particular es dada por su localización en la gráfica. Si se asume que la estadística trazada está distribuida normalmente, la probabilidad de un valor que miente más allá de:
- Los límites amonestadores son la aproximadamente ocasión 0,025 o 2,5%
- Los límites de control son aproximadamente 0,001 o 0,1% ocasiones, éste es raro e indica eso
- La variación es debido a una causa asignable
- El proceso está fuera del control estadístico
Las reglas del funcionamiento
Son las reglas que se utilizan para indicar situaciones fuera del control estadístico.
Las reglas típicas del funcionamiento para las gráficas X de Shewhart con límites del control y advertencia son:
- un punto que miente más allá de los límites de control
- 2 puntos consecutivos que mienten más allá de los límites de advertencia (0.025×0.025×100 = 0,06% oportunidades de ocurrir)
- 7 puntos o más consecutivos que mienten en un lado del medio (0,5 7×100 = 0,8% oportunidades de ocurrir e indica un cambio en el medio del proceso)
- 5 o 6 puntos consecutivos que entran en la misma dirección (indica una tendencia)
- Otras reglas del funcionamiento se pueden formular usando principios similares
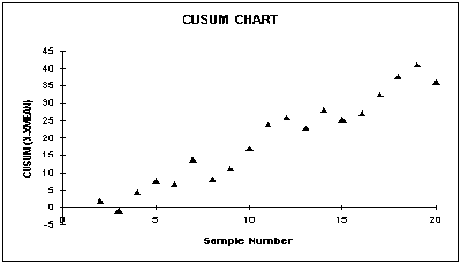
Las gráficas de CUSUM
Son excelentes para detectar cambios en medios. Una gráfica de CUSUM es simplemente un diagrama de la suma de un cierto proceso característico contra tiempo.
Ejemplos de gráficas de control:
Bibliografía