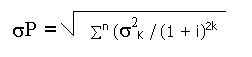El riesgo y la incertidumbre hacen parte in excluible del análisis financiero de proyectos, por ello es necesario conocer las herramientas y los instrumentos que se desarrollan para facilitar la toma de decisiones
Las situaciones a las que a diario se enfrenta el administrador financiero en cuanto a la toma de decisiones con respecto a la evaluación de proyectos es muy compleja, pero la mayoría de estas decisiones son tomadas en condiciones de certeza, en flujos de caja futuros con probabilidad 1.
Sin embargo casi siempre existe el factor incertidumbre en el resultado final de una inversión el cual es muy difícil cuantificar matemáticamente, debido a que en proyectos nuevos casi siempre no hay una base de información a priori y en proyectos que ya se han aplicado, no se puede aducir que la experiencia de otros proyectos sean fiel reflejo de lo que va a ocurrir con el proyecto, ya que en asuntos económicos pueden cambiar muchas condiciones sociales, técnicas, tecnológicas, tributarias etc.
Múltiples escenarios
Cuando se analiza un proyecto deben evaluarse todos sus fundamentos dentro del marco económico real, crítico y de prosperidad
Distribución de probabilidad
Toda decisión de invertir implica pronosticar el futuro y este pronóstico puede hacerse en forma optimista denominada la mejor estimación, en forma realista denominada la estimación más probable o en forma pesimista denominada la peor estimación, estas se pueden presentar cuando la economía está en prosperidad, normal y en represión.
En la distribución de probabilidad, a cada resultado posible se le asigna una probabilidad y la suma de todas las probabilidades es igual a 1.
Cuando un proyecto va a ser evaluado en condiciones de riesgo es porque la asignación de probabilidades se ha hecho en forma objetiva, es decir utilizando métodos estadísticos, pero cuando la asignación de probabilidades se hace de forma subjetiva por un experto en esa clase de proyectos, pero en casi todos los proyectos la asignación de probabilidades se hace subjetivamente.
Valor esperado
Se entiende por valor esperado al medio aritmético probabilístico el cual puede ser calculado con la siguiente fórmula:
XE = ån XK . PK
Donde:
XE = Valor esperado.
XK = Valor del resultado K.
PK = Probabilidad del resultado K.
n = Número total de resultados.
Desviación estándar
Cuando hay varios resultados posibles y éstos están muy dispersos se ve claramente que hay inseguridad en el resultado final de un proyecto, mientras más concentrados estén los resultados habrá más confianza en el resultado final y mientras más dispersos estén los resultados más desconfianza habrá en el resultado final.
La desviación estándar es la medida más adecuada para esta clase de dispersiones y según la estadística se puede calcular con la siguiente fórmula:
Donde:
s = Valor esperado.
XK = Valor del resultado K.
XE = Probabilidad del resultado K.
PK = Número total de resultados.
En casi todos los proyectos financieros la asignación de probabilidades se hace de forma subjetiva
Coeficiente de variación
Cuando se trata de comparar dos a más proyectos en los cuales sus valores son diferentes, se utiliza el coeficiente de variación para realizar el análisis de proyectos financieros. Este está dado por la división de la desviación estándar entre el valor esperado, esto es:
CV = s/XE
Para escoger el mejor proyecto se toma el que tiene menor coeficiente de variación, ya que este es el que tiene un menor riesgo.
Incertidumbre vs. Evaluación de proyectos
Para medir la incertidumbre que se presenta en la evaluación de proyectos se encuentran diferentes metodologías, las más importantes son:
- El método del valor presente neto esperado.
- El método de la probabilidad de pérdida en la aceptación.
- El método de la tasa incrementada por el riesgo.
Método del valor presente neto esperado (VPNE)
El método del valor presente neto esperado es el más usado porque permite incorporar en forma directa el riesgo a la incertidumbre y se basa en el siguiente principio:
VPNE = ån XEK / (1 + i)K
Donde:
VPNE = Valor presente neto esperado.
XEK = Valor esperado en el periodo K.
i = Tasa efectiva para el periodo.
n = Número total de periodos.
Método de la probabilidad de pérdida en la aceptación
El método de la probabilidad de pérdida en la aceptación consiste en hallar la probabilidad del que el VPNE resulte menor de cero y por lo tanto que haya pérdida.
En este método es necesario que se calcule la desviación estándar de todo el proyecto y que se normalicen los resultados para poderle aplicar la curva normal y de esta forma averiguar el área que corresponde a una abcisa menor de cero.
La desviación estándar en este método, depende de las desviaciones de los flujos de caja de cada periodo y puede ser calculada por la siguiente fórmula:
sP = Desviación estándar de todo el proyecto.
sK = Desviación estándar del flujo de caja del periodo K.
n = Número de periodos.
i = Tasa de interés.
Método de la tasa incrementada por el riesgo
El método de la tasa incrementada por el riesgo también llamado método de la tasa ajustada al riesgo, consiste en evaluar el proyecto con una tasa que se debe ser igual a la tasa libre de riesgo más la tasa propia del riesgo.
La tasa libre de riesgo puede ser la tasa que se utilizaría en el proyecto cuando hay certeza y la tasa propia de riesgo es el recargo que debe hacerse por la existencia misma del riesgo, se tiene entonces:
i = i1 + i2
Donde:
i = Tasa ajustada al riesgo.
i1= Tasa libre de riesgo.
i2= Tasa de riesgo.
En este caso se habla de riesgo y no de incertidumbre, porque la tasa i2 puede ser calculada objetivamente por métodos estadísticos.
Es obvio que al aumentar la tasa resulta más difícil que el proyecto sea aprobado, por tanto la tasa i2 debe ser unos puntos adicionales de porcentaje a fin de tener un margen de seguridad que compense posibles errores de juicio pero conduce a unos criterios fijos e independientes de los cambios en el mercado financiero.
Para el cálculo de la tasa i2 y haciendo la suposición de que las condiciones económicas del país sean estables, se hace una estimación con base en datos históricos, esto significa que se debe averiguar cuál fue la tasa que se presento en riesgos similares para aplicarla al nuevo proyecto.