1. Introducción
Día a día nuestro mundo es invadido por un sin fin de información que surge con las nuevas tecnologías e investigaciones, ya que es inevitable que mediante un análisis o tratamiento de información se genere nueva información.
Pero entre toda esa información, existe un gran porcentaje de la misma que no puede ser cuantificable al carecer de precisión o exactitud; ya que esta se caracteriza por ser tan ambigua.
Por lo tanto es normal que una organización posea en sus bases de datos información imprecisa o mejor conocida como información difusa; ya que el ser humano está acostumbrado a incluir en su lenguaje términos o adjetivos que no pueden ser medidos; pero que sin embargo son de gran ayuda para los seres humanos durante la toma de decisiones.
Pero en un mundo tan rápido, es imposible que el ser humano analice toda la información de su organización para tomar decisiones adecuadas en tiempos cortos; por lo cual este proceso de análisis ha sido reemplazado y ahora puede ser realizado por los ordenadores o software.
Pero para que se pueda desarrollar este proceso, es necesario implementar la lógica difusa o la teoría de conjuntos difusos. En el artículo siguiente se explicará ¿Qué es la lógica difusa?.
2. Marco conceptual
2.1 Información
La información es un conjunto de datos acerca de algún suceso, hecho o fenómeno, que organizados en un contexto determinado tienen su significado, cuyo propósito puede ser el de reducir la incertidumbre o incrementar el conocimiento acerca de algo (Thompson, 2008).
2.2 Difusa
Es un adjetivo que hace referencia a que es poco claro, confuso, inexacto, poco concreto al carecer de una buena definición o certeza.
2.3 Lógica difusa
La lógica difusa juega un gran papel en el desarrollo e interpretación de la información difusa, por lo cual es necesario conocer ¿Qué es la lógica difusa? y ¿Dónde surge?
La lógica difusa o mejor conocida como fuzzy logic, que en español se refiere a la lógica borrosa o lógica heurística , trata los conocimientos o información que carecen de exactitud, pero esto no significa que por carecer de precisión la información se tenga que desechar.
Pues entonces entraríamos en una gran controversia, pues es sorprendentemente exorbitante la cantidad de información difusa que manejan y analizan los seres humanos para tomar decisiones en su vida cotidiana.
La lógica difusa es una técnica de la inteligencia computacional que trata de comprender o analizar la información con alto grado de imprecisión.
Con información imprecisa me refiero a la información que está integrada por expresiones como “hace mucho calor”, pero realmente no nos permite saber con exactitud cuánto calor se está experimentado.
La clave para entender ese tipo de expresiones de uso cotidiano por el ser humano radica en la compresión de los cuantificadores de nuestro lenguaje, tales como: “mucho”, “muy”, “escasos”, “pocos”, entre otras.
La lógica difusa se diferencia de la lógica convencional, debido a que la primera procesa la información imprecisa y la segunda procesa solo la información bien definida y precisa.
Lo más sorprendente es que el ser humano si alcanza a comprender las expresiones que hacen que la información sea imprecisa y en base a ellas toma decisiones importantes.
Sin embargo el análisis de los cuantificadores es realizado por los seres humanos aunque el anterior no pueda ser realizado por los ordenadores.
Esto tuvo fin cuando el investigador Lofti A. Zadeh, al no estar conforme con las opciones de los conjuntos clásicos (crisp sets) que solo poseen dos opciones: de pertenencia (1) o que no pertenecen a ni un conjunto (0).
Describió en 1965 por primera vez los “conjuntos difusos” o “fuzzy sets”; donde destaca que los conjuntos pueden pertenecer parcialmente a unos conjuntos, dejando atrás la lógica tradicional o convencional. Dicho concepto fue publicado en el artículo fuzzy sets .
Zadeh establece el concepto de lógica difusa, cuando comprueba la teoría de los conjuntos difusos. Seis años más tarde Zadeh publica en el artículo “Quantitive Fuzzy Semantics”, donde define los elementos que conforman la lógica difusa y sus aplicaciones actuales.
Hay que mencionar que la teoría de conjuntos difusos y el concepto de lógica difusa en sus inicios tuvo gran aceptación en Europa, mientras que en Estados Unidos (que fue su cuna) se negaban aceptar este nuevo descubrimiento; ya que los científicos se mantenían escépticos a todo lo que no fueran teorías binarias.
Pero fue hasta el año 1974, cuando Ebrahim Mandani , aplico por primera vez el concepto de lógica difusa en el campo de control en la industria.
Fue el creador del sistema de control difuso o fuzzy control; llevándolo a la aplicándolo para regular el motor de vapor.
Es de imaginarse que el éxito de Mandani de la aplicación de lógica difusa y los conjuntos difusos fue consecuencia de los avances tecnológicos en los ordenadores (que anteriormente no estaban tan desarrollados).
3. Información difusa
El Ingeniero Zadeh pensaba que las personas no necesitaban información lógica o numérica para realizar tareas de control; sino que para las personas era a veces mucho más práctico desarrollar actividades o tareas con datos imprecisos.
Solo entonces información difusa es aquella información que está conformada por un conjunto de datos difusos o datos borrosos o poco claros, que no son exactos y que no son cuantificables, sin embargo dichos datos son cualitativos y pueden ser medibles.
Es sumamente importante mencionar que la información difusa es de gran importancia para el desarrollo de las organizaciones, ya que esta puede representar una limitante al bloquear que la organización pueda adquirir el verdadero conocimiento a la hora compartirlo o informar.
Un ejemplo de la información difusa o poco clara es cuando los datos interrelacionados no son cuantificables, un ejemplo es el siguiente:
Durante un estudio de mercado deben realizarse preguntas para conocer el grado de aceptación que tendrá un producto en los consumidores.
Mediante las preguntas se pretende conocer las emociones que percibe el consumidor acerca del producto, estas preguntas se encuentran íntimamente relacionadas con una serie de pruebas organolépticas ; la cual nos darán como resultado un conjunto de datos que no son medibles en otras palabras es “información difusa” que no es lo suficientemente clara para poder entenderla.
Hay que mencionar que información difusa no solamente es aquella que no es cuantificable, sino también puede ser toda aquella información lógica que durante su procesamiento o análisis pierda su verdadero significado.
El hecho de que tengamos información difusa, no significa que no se pueda aprovechar o que no tenga valor para la organización, al contrario significa que tenemos que someter dichos datos a otro proceso para poder analizarla y transformarla en información lógica, convencional o tradicional.
Una vez que la información fue transformada en información cuantificable, brindará las herramientas necesarias para que la organización o individuos tomen buenas decisiones.
3.1 Conjunto difuso
El padre de la lógica difusa Zedah, define al conjunto difuso como aquellos ítems que no se sabe a ciencia cierta el grado de pertenencia que posee un ítem a un conjunto, pero que de alguna manera están relacionados.
Un ejemplo es el conjunto de personas altas, esto es un ítem difuso; debido a que no se cuenta con unos parámetros medibles que nos permitan identificar o conocer a partir de qué medida las personas se puede considerar altas para que pertenezcan al conjunto de las personas altas.
Entonces se puede decir que el límite de altura es difuso y al no existir especificaciones o atributos cualquier persona puede entrar en ese conjunto.
Un conjunto difuso se define de la siguiente manera: Un conjunto difuso A sobre un universo de discurso U (ordenado) es un conjunto de pares representado por una ecuación matemática:
A= {µλ (u)/u:u ε U, µλ (u) ε [0,1]},
Donde:
µ=función de pertenencia
µλ= grado de pertenencia del elemento u al conjunto difuso A.
(que va desde 0-1)
µλ (u)=0 indica que u no pertenece en absoluto al conjunto difuso A.
µλ (u)=1 indica que u pertenece totalmente al conjunto difuso A
3.2 Elementos del conjunto difuso
Una vez que explicamos lo que es y la importancia de la información difusa en la organización, es necesario que conozcamos los elementos que posee la información difusa.
Entonces un ítem de información está conformado por (Urrutia & Varas, 2013):
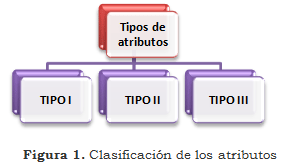
Á Atributos: es una función que determina el valor a un objeto.
Los atributos se clasifican en tres tipos:
Tipo I: Se refiere a los datos precisos o mejor conocidos como clásicos, que pueden tener etiquetas lingüísticas definidas. Ejemplo el de una persona alta.
Tipo II: atributos que almacenan datos clásicos y difusos, al ser un conjunto de datos imprecisos relacionado a un referencial ordenado.
Por ejemplo las etiquetas pueden ser: niño, joven, adulto con referencia sobre un conjunto de 0 a 100.
Tipo III: son atributos sobre datos imprecisos relacionados a un referencial normal no ordenado.
Ejemplo: el atributo sería color del cabello y el referencial no ordenado o las etiquetas serían; rubios, pelirrojos y castaños.
Los atributos anteriormente mencionados sirven para realizar un modelo para tratar los conjuntos difusos.
- Objeto: puede ser cualquier cosa o ítem.
- Valor: es un subconjunto del dominio de referencia asociado al atributo (Garrido & Cadenas, 2013).
- Confianza: es un indicador del grado de veracidad del ítem.
3.3 Características de la información difusa
La información difusa se caracteriza por ser imprecisa y poseer un alto grado de incertidumbre, la diferencia entre estas dos características radica en que la imprecisión está relacionada con el valor de ítem y la incertidumbre es un indicador de confianza del ítem.
3.4 ¿Cómo reconocer la información difusa de la convencional?
Es normal que durante la etapa de la recolección de la información se obtenga todo tipo de información tanto lógica como difusa, ya que una organización genere una cantidad de información en sus diferentes departamentos y ambiente; externo e interno.
Para determinar si la información obtenida durante el proceso de recolección es difusa, es necesario considerar una serie de cuestionamientos que considerados por Rosas Sánchez (2012):
- ¿La información obtenida satisface las necesidades de la organización?
- ¿La información puede ser consultada de una forma eficiente por los colaboradores que la requieran?
- ¿La información es concreta, confiable y está completamente integrada?
- ¿Presenta alguna duplicidad?
3.5 Herramientas para la identificación y extracción de la información difusa
La secuencia de pasos que a continuación se describirán, son aplicados para la identificación y extracción de la información difusa de la convencional, con la finalidad de obtener solo la información difusa y a continuación se pueda procesar y trabajar en la información difusa para transformarla en información lógica.
- Asignar personal que se encargue de analizar la información pertinente de cada actividad.
- Consultar al personal experto en el desarrollo de un método para la gestión de la información en la organización.
- Implementar un método para recolectar, recopilar toda la información y que la estructure y ordene jerárquicamente.
- Determinar las fuentes de información que se están manejando.
- Medir la confiabilidad de las fuentes de información.
- Implementar técnicas de lectura rápida y selección para subrayar las ideas principales, dentro de las cuales se deben identificar las “key words” .
- Diseñar fichas de contenido.
- Utilizar índices y buscadores temáticos.
3.6 Herramientas para analizar la información difusa
Una vez que ya fueron identificada y extraída la información difusa es necesario implementar otro tipo de herramientas para realizar el análisis o la conversión de información difusa en información convencional; convirtiéndose esta a su vez en conocimiento para la organización.
3.6.1 Análisis de datos cuantitativos
La información cuantitativa por lo general no es difusa, debido al grado de precisión y confiabilidad que posee ya que son medibles; lo que se tiene que hacer para evitar que la información cuantitativa se convierta en difusa es implementar un software que facilite la manipulación de los conjuntos de datos numéricos, con la finalidad de que se mantenga su confiabilidad y certeza para la toma de decisiones.
3.6.2 Análisis de datos cualitativos
El análisis de estos datos es más complicado, debido a la ausencia de certeza, confiabilidad y ya que los datos del conjunto difuso no poseen una estructura limitada o pertenencia.
En otras palabras los datos cualitativos no son medibles, por lo que complican su análisis para su estudio, al ser solo conceptos subjetivos, volviéndose difuso su conocimiento.
3.6.3 Métodos heurísticos
Los métodos heurísticos sirven para implementar un método creativo para la resolución de problemas difusos, entre los cuales se encuentra el método Silver meal, las heurísticas proporcionan mejores soluciones cuando son ejecutadas mediante un software obteniendo la solución ideal.
3.6.4 Lógica difusa
Es uno de los métodos más recientes para analizar la información cualitativa o imprecisa. Este método es muy utilizado cuando un concepto posee diferentes significados según el tiempo y contexto. La base de la lógica difusa son los conjuntos difusos por Zadeh mencionados anteriormente.
3.7 Modelo de un sistema basado en técnicas de lógica difusa
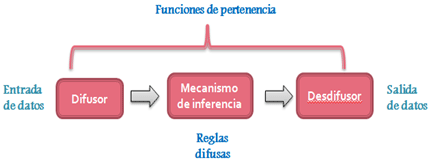
El modelo del sistema basado en técnicas de lógica difusa está conformada por tres bloques (véase figura 2):
Difusión
Inferencia
Desdifusión
En la figura 2 se muestra un sistema el cual inicia con la entrada de datos que está conformada por el conjunto de variables, que previamente fueron seleccionadas según las especificaciones del problema a resolver. Un ejemplo serían los factores relacionados con el transporte en un espacio urbano: población, número de vehículos, viviendas, empleo.
3.7.1 Bloque difusor
Tiene la función de conformar conjuntos difusos, según el grado de pertenencia que posea cada variable de la entrada (ingresadas individualmente) se decidirá en que conjunto difuso se colocarán.
3.7.2 Bloque de inferencia
Tiene la función de relacionar o indicar el cumplimiento de una proposición con otra, lo cual se representa p q, de esta forma se puede expresar Si… entonces.
Por lo tanto el bloque de inferencia expresa reglas difusas como Si u es A entonces v es B, donde A y B son conjuntos difusos; donde u ε U y v ε V.
El objetivo final es transformar los conjuntos difusos formados por el bloque anterior según el grado de pertenencia en conjuntos difusos asociados a una variable de salida.
3.7.3 Bloque de desdifusión
Una vez que los conjuntos difusos fueron asociados a una variable de salida, es necesario expresar de forma concreta los resultados obtenidos.
Es importante mencionar que esta etapa se puede realizar mediante tres métodos:
Corte a: consiste en una reducción del total de valores a un solo conjunto.
Valor máximo: el conjunto solo posee un valor máximo, encaso de que existieran diverso valores máximos es necesario tomar los valores de los promedios.
Centroide: centro de gravedad, calculado con sumatorias.
Salidas: son los resultados concretos, que en el ejemplo sería conocer o identificar el tráfico vehicular respecto al número de viajes urbanos.
3.8 Comunicación de la información difusa
La comunicación es esencial en cualquier proceso dentro de la organización y la comunicación de la información difusa no es la excepción, ya que se debe buscar la forma de eludir que la organización posea más información difusa que la lógica.
Por tal motivo se recomienda que una vez que la organización analizo y cuantifico la información difusa, los colaboradores que son afectadas positivamente o negativamente sean informados de los resultados concretos obtenidos al final.
3.9 Ejemplo de la teoría de conjuntos difusos
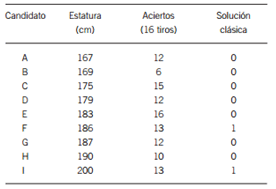
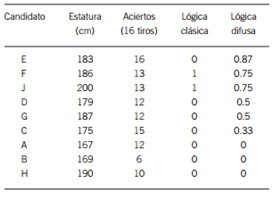
Un entrenador de baloncesto debe seleccionar candidatos para su equipo, las especificaciones o parámetros que deben cumplir los jugadores para pertenecer a la selección son: altura ≥1.85 m y encestar ≥13 canastas de 16 (véase tabla 1).
Tabla 1. Resultados obtenidos de la prueba (D´Negri & de Vito, 2006).
La solución clásica solo tomaría a los candidatos I y F; sin embargo el candidato E encesto 16 de 16, pero no contar con la estatura limite se queda fuera de la solución.
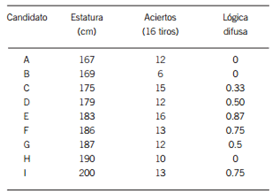
La solución resultante por aplicar conjuntos difusos es diferente, primero de debe definir números difusos para cada variable que van del 0 a 1 según el grado de pertenencia al conjunto de altura ≥1.85 m y encestar ≥13 canastas de 16, obteniendo al final una combinación por lógica difusa.
Entonces aplicando la teoría de conjuntos nos podemos dar cuenta que obtenemos otra solución; donde el jugador E forma parte de la solución final, mientras que por la otra solución clásica quedaría fuera un buen elemento por 2 cm.
Tabla 2. Solución por lógica difusa (D´Negri & de Vito, 2006)
La diferencia entre ambos métodos consiste en la graduación, mientras que en la solución clásica las graduaciones son 0 o 1 (pertenece o no pertenece), la solución por teoría de conjuntos difusos la graduación es intermedia entre 0 a 1; ampliando el grado de pertenencia al conjunto difuso (véase tabla 3).
Tabla 3. Comparación de la escala de graduación obtenida a través de la lógica clásica y la lógica difusa (D´Negri & de Vito, 2006).
3.9.1 Ejemplos de la aplicación de información difusa en la industria aplicando lógica difusa.
Japón es el país que ha implementado la lógica difusa para la solución de problemas de información difusa, a continuación enumeran.
- Sistemas de control de aires acondicionados.
- Sistema de foco automático en cámaras fotográficas.
- Optimización de sistemas de control industriales.
- Sistema de reconocimiento de escritura.
- Mejoramiento eficiente en el uso del combustible.
- Simulación del comportamiento humano
- Almacenar y consultar información imprecisa (FSQL).
- Aplicación de lógica difusa por parte de la NASA para realizar maniobras complejas
- Sistemas de mantenimiento: Para infraestructura que estén relacionado con las fallas o el mantenimiento; llámense puentes, estructuras metálicas, carreteras.
- Sistemas de control.
Sistemas de control (decisiones para regulación, por ejemplo en tráfico, depósitos de agua, compuertas).
Cálculos con entradas difusas (cargas en vías y puentes, solicitaciones sísmicas, estabilidad de taludes).
En medicina
- Evaluación del envejecimiento arterial mediante señales de la arteria, utilizando registros incruentos.
- Clasificación del registro para evaluar costos institucionales de diabéticos internados.
- Técnicas difusas para el análisis de datos biomédicos.
4. Conclusión
Como en otras ocasiones ya lo había mencionado que la información es el activo más importante dentro de las organizaciones y es el activo que define el grado de ventaja competitiva que posee cada organización.
Pero esto no significa que la organización por el simple hecho de que posee una gran cantidad de información tendrá una ventaja competitiva sobre sus demás competidores.
Pues de nada nos sirve tener información que no se puede medir el impacto que puede ocasionar una determinada variable o de la misma forma es inútil poseer con una gran cantidad de información convencional si no se le realizo el proceso correcto y por lo tanto no se tiene un grado de confianza alto ni en la información que se supone que es cien por ciento confiable, ya que ocasiona que los colaboradores de la organización se pierdan entre los mares de información que posee.
Entonces la organización puede poseer dos tipos de información; la información lógica o convencional (que es cuantificable) y la información difusa que se caracteriza por no ser cuantificable y por ser una información que carece de precisión.
Sin embargo, la información difusa es de gran importancia para la organización por lo cual es necesario que dicha información sea sometida a un proceso de transformación de información difusa en información concreta que sirva como conocimiento a la organización y a su vez le permita tomar decisiones correctas.
El análisis de la información difusa, tiene sus bases en la lógica difusa.
5. Propuesta de tesis:
Implementar lógica difusa para determinar las causas que ocasionan las fallas más concurrentes en los ductos en PEMEX, Cd. Mendoza.
5.1 Objetivo:
Transformar la información difusa en información convencional que sirva como conocimiento para el personal de emergencias, con la finalidad de volver más eficiente los procesos productivos.
6. Referencias bibliográficas
- Arriola Carrera, G. A. (2013). Obtenido de http://es.scribd.com/doc/57256980/INFORMACION-DIFUSA
- Cancino Velásquez, J. A. (5 de Mayo de 2012). Comunicación y manejo de información difusa. Obtenido de Gestiopolis: https://www.gestiopolis.com/administracion-estrategia-2/comunicacion-manejo-de-informacion-difusa.htm
- Civil, I. (28 de Abril de 2013). Elementos sobre conjuntos difusos y lógica difusa.
- D´Negri, C. E., & de Vito, E. L. (2006). Introducción al razonamiento aproximado: lógica difusa. Obtenido de Revista Argentina de Medicina Respiratoria:
- Garrido, & Cadenas, J. M. (28 de Abril de 2013). Tratamiento de información difusa en un modelo de mezcla de componentes de gaussianas.
- Rosas Sánchez, L. (14 de Marzo de 2012). Manejo de información difusa. Herramienta indispensable para la toma de decisiones. Obtenido de Gestiopolis: https://www.gestiopolis.com/administracion-estrategia-2/manejo-informacion-difusa-herramienta-indispensable-toma-decisiones.htm
- Thompson, I. (2008). Promonegocios. Obtenido de http://www.promonegocios.net/mercadotecnia/definicion-informacion.html
- UDLAP. (29 de Abril de 2013). Lógica difusa. Obtenido de Capitulo 3: http://catarina.udlap.mx/u_dl_a/tales/documentos/lmt/ramirez_r_o/capitulo3.pdf
- Urrutia, A., & Varas, M. (28 de Abril de 2013). Modelo de Datos Difusos en UML: Un caso de Asesoramiento para Inserción de Publicidad. Obtenido de