Introducción
La programación lineal es un conjunto de técnicas racionales de análisis y de resolución de problemas que tiene por objeto ayudar a los responsables en las decisiones sobre asuntos en los que interviene un gran número de variables.
El nombre de programación lineal no procede de la creación de programas de ordenador, sino de un término militar, programar, que significa “realizar planes o propuestas de tiempo para el entrenamiento, la logística o el despliegue de las unidades de combate”.
Aunque parece ser que la programación lineal fue utilizada por G. Monge en 1776, se considera a L. V. Kantoróvich uno de sus creadores. La presentó en su libro Métodos matemáticos para la organización y la producción (1939) y la desarrolló en su trabajo Sobre la transferencia de masas (1942). Kantoróvich recibió el premio Nobel de economía en 1975 por sus aportaciones al problema de la asignación óptima de recursos humanos.
La investigación de operaciones en general y la programación lineal en particular recibieron un gran impulso gracias a los ordenadores. Uno de momentos más importantes fue la aparición del método del simplex.
Objetivos
- Conocer la programación lineal y sus aplicaciones a la vida cotidiana.
- Plantear y resolver situaciones con programación lineal.
- Pasos para la construcción de un modelo.
Tipo de Soluciones
Los programas lineales con dos variables suelen clasificarse atendiendo al tipo de solución que presentan. Éstos pueden ser:
- Factibles: Si existe el conjunto de soluciones o valores que satisfacen las restricciones. Estas a su vez pueden ser: con solución única, consolución múltiple (si existe más de una solución) y con solución no acotada (cuando no existe límite para la función objetivo).
- No factibles: Cuando no existe el conjunto de soluciones que cumplen las restricciones, es decir, cuando las restricciones son inconsistentes.
Métodos de solución
Existen tres métodos de solución de problemas de programación lineal:
- Método gráfico: Las rectas de nivel dan los puntos del plano en los que la función objetivo toma el mismo valor.
- Método analítico: El siguiente resultado, denominado teorema fundamental de la programación lineal, nos permite conocer otro método de solucionar un programa con dos variables: “en un programa lineal con dos variables, si existe una solución única que optimice la función objetivo, esta se encuentra en un punto extremo (vértice) de la región factible acotada, nunca en el interior de dicha región. Si la función objetivo toma el mismo valor óptimo en dos vértices, también toma idéntico valor en los puntos del segmento que determinan. En el caso de que la región factible no es acotada, la función lineal objetivo no alcanza necesariamente un valor optimo concreto, pero, si lo hace este se encuentra en uno de los vértices de la región”.
- Esquema práctico: Los problemas de programación lineal puede presentarse en la forma estándar, dando la función, objetivos y las restricciones, o bien plantearlos mediante un enunciado.
Estructura básica:
Ejemplos de programación lineal tomados de:
Unos grandes almacenes encargan a un fabricante pantalones y chaquetas deportivas.
El fabricante dispone para confección de 750 m de tejido de algodón y 1000 m de tejido de poliéster. Cada pantalón precisa 1 m de algodón y 2 m de poliéster. Para cada chaqueta se necesita 1.5 m de algodón y 1 m de poliéster.
El precio del pantalón se fija en $ 50 y de la chaqueta en $40.
¿Qué número de pantalones y chaquetas debe suministrar el fabricante a los almacenes para que estos consignan una venta máxima?
1. Elección de las incógnitas.
- X= número de pantalones
- Y= número de chaquetas
2. Función objetivo
- F(x,y)=50x + 40y
3. Restricciones
Para escribir las restricciones vamos a ayudarnos de una tabla:
| Pantalones | Chaquetas | Disponibles | |
|
Algodón |
1 |
1.5 |
750 |
|
Poliéster |
2 |
1 |
1000 |
- X + 1.5y < 750 à 2x + 3y< 1500
- 2x + y < 1000
Como el número de pantalones y chaquetas son números naturales, tendremos dos restricciones más:
- X>0
- Y>0
4. Halla el conjunto de soluciones factibles
Tenemos que representar gráficamente las restricciones.
Al ser x > 0 e y > 0, trabajaremos en el primer cuadrante.
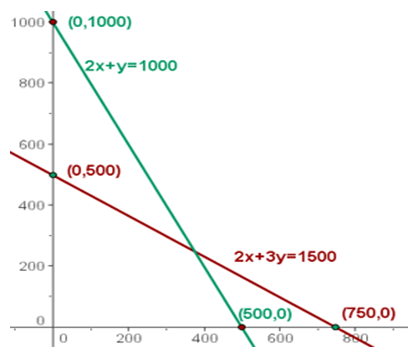
Representamos las rectas, a partir de sus puntos de corte con los ejes.
Resolvemos gráficamente la inecuación: 2x + 3y < 1500, para ello tomamos un punto del plano, por ejemplo el (0,0).
Como 0 < 1500 entonces el punto (0,0) se encuentra en el semiplano donde se cumple la desigualdad.
De modo análogo resolver 2x + y < 1000.
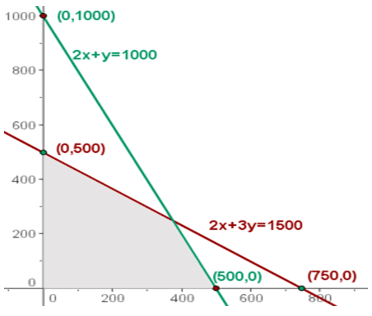
La zona de intersección de las soluciones de las inecuaciones sería la solución al sistema de inecuaciones, que constituye el conjunto de las soluciones factibles.
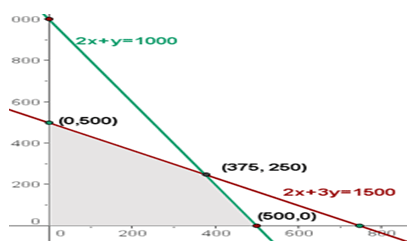
5. Calcular las coordenadas de los vértices del recinto de las soluciones factibles.
La solución óptima, si es única, se encuentra en un vértice del recinto. Estos son las soluciones a los sistemas:
2x + 3y = 1500; x= 0 (0,500)
2x + y = 1000; y= 0 (500,0)
2x + 3y = 1500; 2x + y = 1000 (375, 250)
6. Calcular el valor de la función objetivo
En la función objetivo sustituimos cada uno de los vértices.
- F(x,y) = 50x + 40y
- F(0,500) = 50*0 + 40*500 = $20000
- F(500,0) = 50*500 + 40*0 = $ 25000
- F(375,250) = 50*375 + 40*250 = $28750
La solución óptima es fabricar 375 pantalones y 250 chaquetas para obtener un beneficio de $ 28750.
Bibliografía:
Ejemplos de programación lineal tomados de: