El uso estadístico del coeficiente de correlación y la regresión lineal, nos indican que tan relacionadas se encuentran dos variables en una muestra, a continuación se ejemplifica su uso y se enseñan los pasos para resolverlos gráficamente a través del uso del software MINITAB.
Se quiere ofrecer al alumno las herramientas gráficas y estadísticas que le permitan aprender a manejar, analizar e interpretar los datos con el software MINITAB 14. No es una práctica de estadística, no es una práctica de calidad, sino una práctica para aprender a usar el software MINITAB en esas aplicaciones. Conoceremos conceptos de calidad y conceptos de estadística que son necesarios para el mejor entendimiento del programa.
Aprenderá a importar/exportar datos y resultados entre Minitab y distintos programas. Incrementará su habilidad de crear, manipular y reestructurar datos. Desarrollará la habilidad para seleccionar la herramienta adecuada para analizar sus datos y aprenderá a crear e interpretar una gran variedad de gráficas y medidas numéricas utilizadas en iniciativas de mejoramiento de la calidad.
Definiciones introductorias:
Variable
Una variable es un símbolo que representa un elemento no especificado de un conjunto dado. Dicho conjunto es llamado conjunto universal de la variable, universo o dominio de la variable, y cada elemento del conjunto es un valor de la variable. Sea x una variable cuyo universo es el conjunto {1,3,5,7,9,11,13}; entonces x puede tener cualquiera de esos valores: 1,3,5,7,9,11,13. En otras palabras x puede reemplazarse por cualquier entero positivo impar menor que 14. Por esta razón, a menudo se dice que una variable es un reemplazo de cualquier elemento de su universo.
Medición
La medición es la determinación de la proporción entre la dimensión o suceso de un objeto y una determinada unidad de medida. La dimensión del objeto y la unidad deben ser de la misma magnitud. Una parte importante de la medición es la estimación de error o análisis de errores.
Diagramas de dispersión (incluir dibujos)
Un diagrama de dispersión es una representación gráfica de la relación entre dos variables, muy utilizada en las fases de Comprobación de teorías e identificación de causas raíz y en el Diseño de soluciones y mantenimiento de los resultados obtenidos.
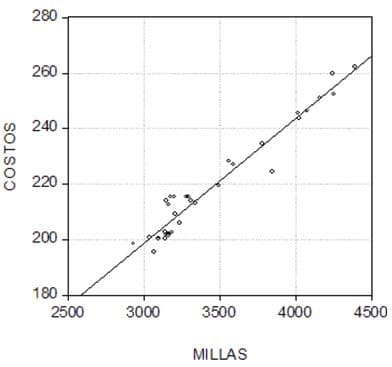
Correlación y regresión lineal – Diagrama de dispersión
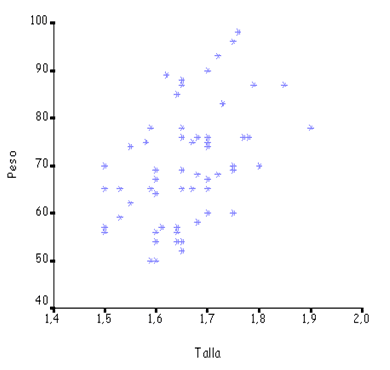
Correlación y regresión lineal – Diagrama de dispersión
Coeficiente de correlación
El coeficiente de correlación provee una medida de como dos variables aleatorias están asociadas en una «muestra». Es también una medida de la intensidad de la relación lineal entre X y Y.
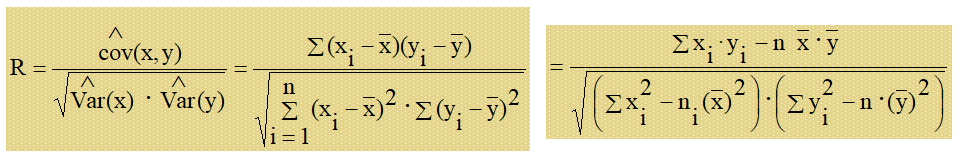
Correlación y regresión lineal – Coeficiente de correlación
Regresión entre dos variables
Este tipo se presenta cuando dos o más variables independientes influyen sobre una variable dependiente. Ejemplo: Y = f(x, w, z).
Por ejemplo: Podría ser una regresión de tipo múltiple:
Una empresa de desarrollo de software establece relacionar sus ventas en función del número de pedidos de los tipos de software que desarrolla (sistemas, educativos y automatizaciones empresariales), para atender 10 proyectos en el presente año.
En la Tabla representa Y (Ventas miles de S/.) y X (Nº pedidos de sistemas), W (Nº de pedidos de Aplicaciones Educativas) y Z (Nº de pedidos de Automatizaciones empresariales).
Ejemplos teóricos
- El profesor Isaac Asimov fue uno de los escritores más prolíficos de todos los tiempos. Para cuando murió (1992) había escrito casi 500 libros a lo largo de una carrera de 40 años. De hecho, a medida que avanzaba en su profesión se volvió más productivo en términos de la cantidad de libros escritos en un lapso dado. Estos datos son los tiempos que requería para escribir sus libros, en incrementos de 100:
a. Grafique la cantidad acumulada de libros en función del tiempo mediante un diagrama de dispersión.
| Número de libros | 100 | 200 | 300 | 400 | 490 |
| Tiempo (en meses) | 237 | 350 | 419 | 465 | 507 |
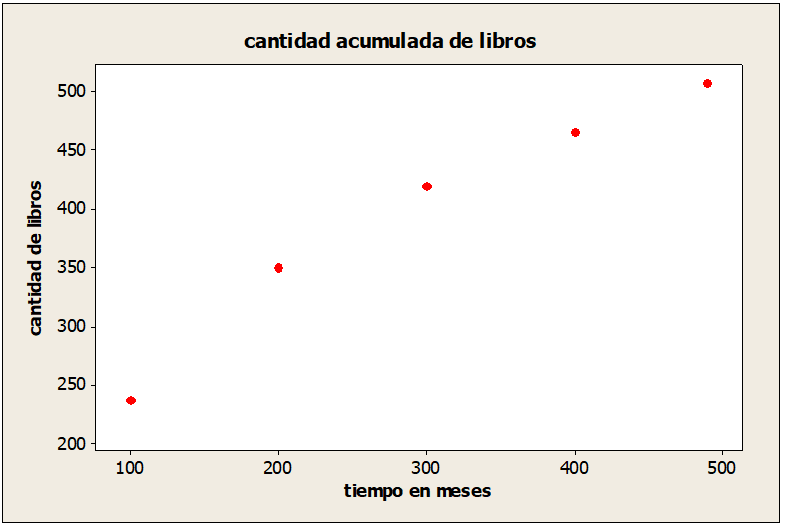
Correlación y regresión lineal – Diagrama de dispersión
b. Describa la productividad del profesor Asimov con base al conjunto de datos graficados en el inciso a). ¿La relación entre las dos variables parece ser lineal?
Al parecer la relación entre las dos variables si tiene signos de ser lineal, esto se comprueba con tan solo mirar el diagrama de dispersión y darse cuenta de que los puntos en el diagrama forman una línea casi recta en aumento con relación al tiempo en meses y la cantidad de libros.
- La materia prima que se usa en la elaboración de una fibra sintética se almacena en un local que no tiene control de humedad. Las mediciones de la humedad relativa en el local y del contenido de humedad de una muestra de la materia prima (ambos en porcentajes) durante 12 días, dieron los siguientes resultados:
| Humedad, X | Contenido de Humedad, Y |
| 42 | 12 |
| 35 | 8 |
| 50 | 14 |
| 43 | 9 |
| 48 | 11 |
| 62 | 16 |
| 31 | 7 |
| 36 | 9 |
| 44 | 12 |
| 39 | 10 |
| 55 | 13 |
| 48 | 11 |
Ajuste una línea recta y determine el contenido de humedad cuando la humedad del local de almacenamiento es de 40%.
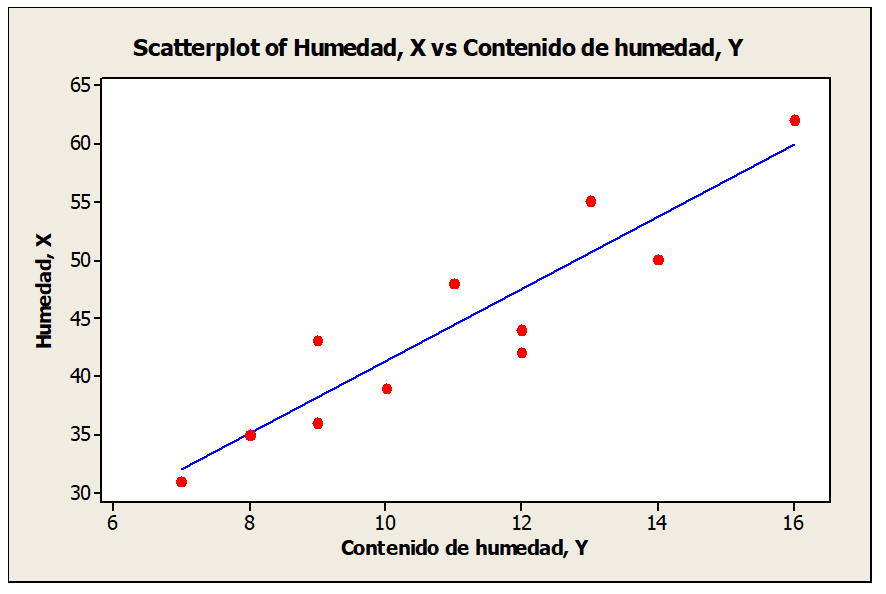
Correlación y regresión lineal – Ajuste de línea recta
- Los estadounidenses conscientes de la salud consultan a menudo la información relacionada con los nutrientes que aparecen en los envases de los alimentos con el fin de evitar los que contengan grandes cantidades de grasa, sodio o colesterol. La siguiente información se tomó de ocho marcas distintas de queso americano en rebanadas:
| Marca | Grasa (g) | GrasasSaturadas (g) | Colesterol(mg) | Sodio (mg) | Calorías |
| Kraft Deluxe American | 7 | 4.5 | 20 | 340 | 80 |
| Kraft Velveeta Slices | 5 | 3.5 | 15 | 300 | 70 |
| Private Selection | 8 | 5.0 | 25 | 520 | 100 |
| Ralphs Singles | 4 | 2.5 | 15 | 340 | 60 |
| Kraft 2% Milk Singles | 3 | 2.0 | 10 | 320 | 50 |
| Kraft Singles American | 5 | 3.5 | 15 | 290 | 70 |
| Borden Singles | 5 | 3.0 | 15 | 260 | 60 |
| Lake to Lake American | 5 | 3.5 | 15 | 330 | 70 |
a. ¿Qué pares de variables espera usted que estén fuertemente relacionadas?
El colesterol y las calorías, porque en tabla se observa que dependiendo la cantidad de colesterol es la cantidad de calorías que contiene cada producto, o podría ser al revés que dependiendo la cantidad de calorías es la cantidad de colesterol que contiene cada producto.
b. Trace un diagrama de dispersión para la grasa y la grasa saturada. Describa la relación.
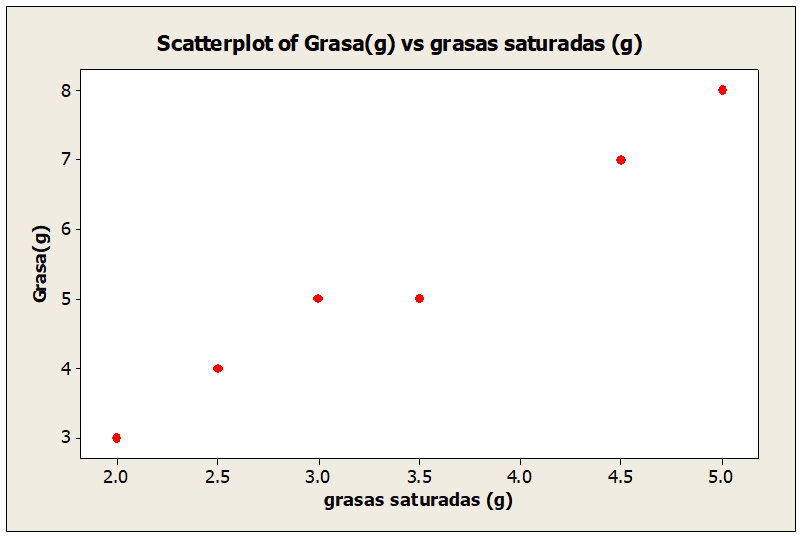
Correlación y regresión lineal – Diagrama de dispersión
c. Elabore un diagrama de dispersión para grasas y calorías. Compare el patrón con el observado en el inciso b).
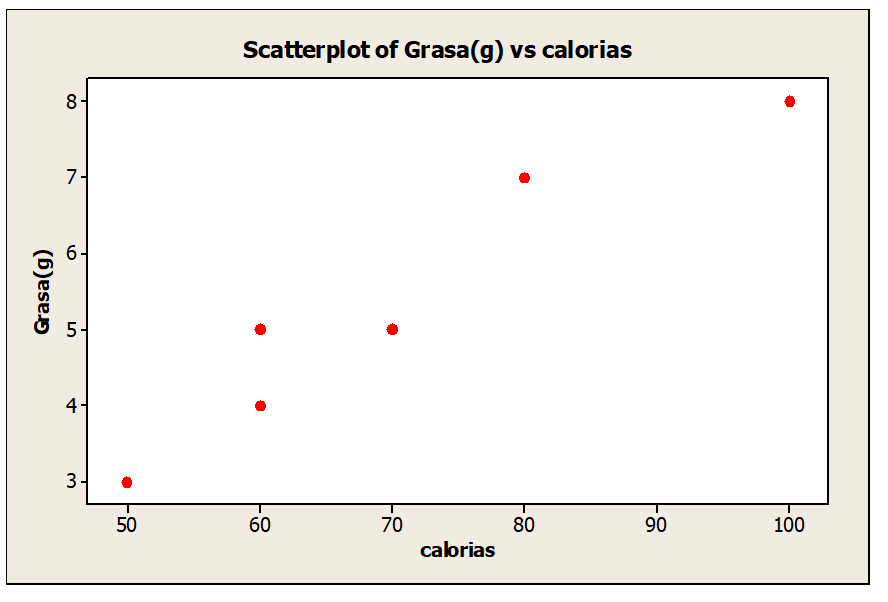
Correlación y regresión lineal – Diagrama de dispersión
d. Trace un diagrama de dispersión para la grasa y el sodio, y otro para colesterol y sodio.
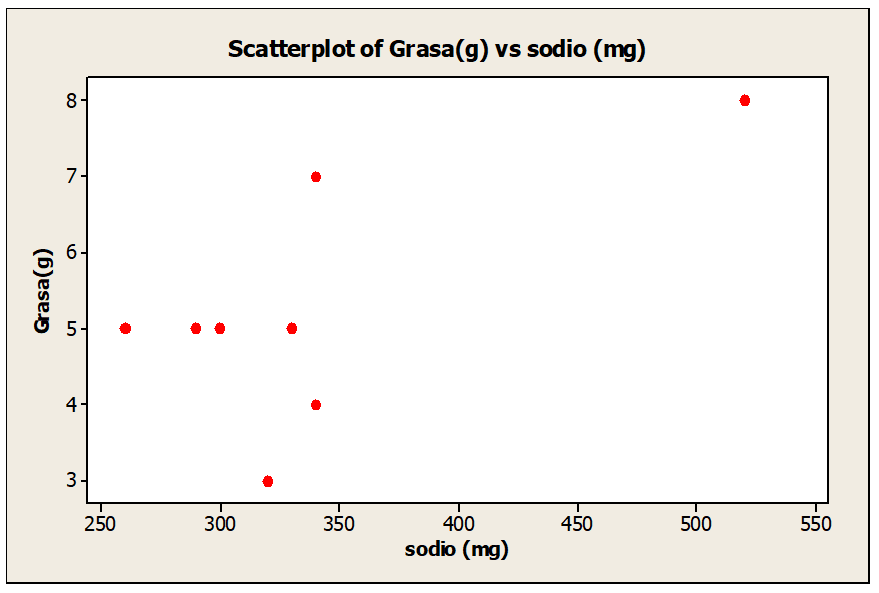
Correlación y regresión lineal – Diagrama de dispersión
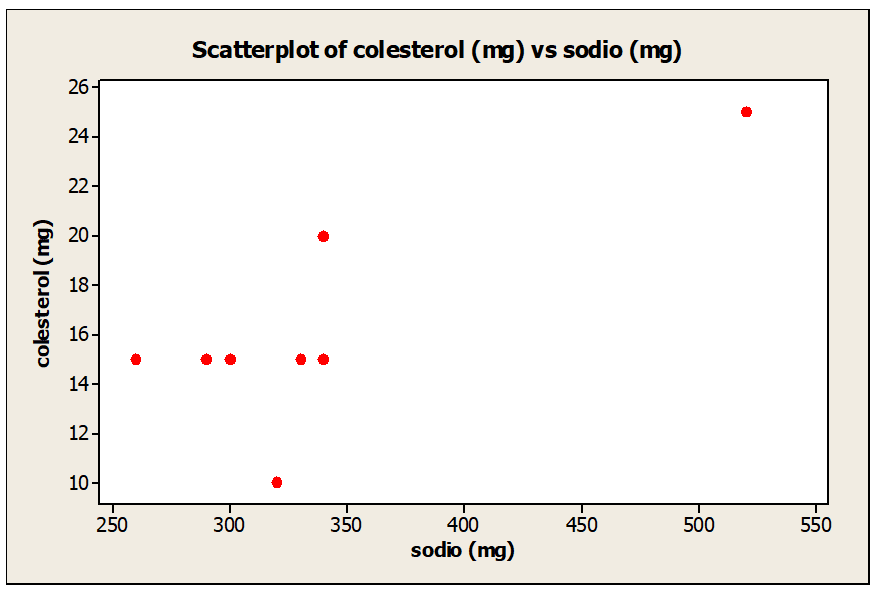
Correlación y regresión lineal – Diagrama de dispersión
e. Calcule el coeficiente de correlación r para las variables de colesterol y sodio.
| Propiedad | X | Y | (X-X) | (X-Xi)2 | (Y-Y) | (Y-Y)2 | (X-X)(Y-Yi) |
| 1 | 20 | 340 | 3.75 | 13.83 | 2.5 | 6.25 | 9.37 |
| 2 | 15 | 300 | -1.25 | 1.56 | -37.5 | 1406.25 | 46.87 |
| 3 | 25 | 520 | 8.75 | 76.56 | 182.5 | 33,306.25 | 1,596.87 |
| 4 | 15 | 340 | -1.25 | 1.56 | 2.5 | 6.25 | -3.125 |
| 5 | 10 | 320 | -6.25 | 39.06 | -17.5 | 306.25 | 109.37 |
| 6 | 15 | 290 | -1.25 | 1.56 | -47-5 | 2,256.25 | 59.37 |
| 7 | 15 | 260 | -1.25 | 1.56 | -77.5 | 6,006.25 | 96.87 |
| 8 | 15 | 330 | -1.25 | 1.56 | -7.5 | 56.25 | 9.37 |
Σ=1,896.84
Xi=Σ x/n
130/8 = 16.25
Yi = Σy /n
2700/8 = 337.5
√ ² Σ(x-xi)2 /n-1
√19.06 = 4.42
√ ² Σ (y-yi)2/n-1
√6,192.85 = 78.69
Covarianza
Sxy = Σ (xi – x)(yi – y) / n -1
1896.84/7 = 270.9771
Coeficiente de correlación
r = Sxy / SxSy
270.97/(4.42)(78.69) = 0.7790
- Suponga que el gerente de una cadena de servicios de entrega de paquetería desea desarrollar un modelo para predecir las ventas semanales (en miles de dólares) para las tiendas individuales basado en el número de clientes que hacen las compras. Se seleccionó una muestra aleatoria entre todas las tiendas de la cadena con los siguientes resultados:
| Tienda | Clientes | Ventas ($1000) |
| 1 | 907 | 11.20 |
| 2 | 926 | 11.05 |
| 3 | 506 | 6.84 |
| 4 | 741 | 9.21 |
| 5 | 789 | 9.42 |
| 6 | 889 | 10.08 |
| 7 | 874 | 9.45 |
| 8 | 510 | 6.73 |
| 9 | 529 | 7.24 |
| 10 | 420 | 6.12 |
| 11 | 679 | 7.63 |
| 12 | 872 | 9.43 |
| 13 | 924 | 9.46 |
| 14 | 607 | 7.64 |
| 15 | 452 | 6.92 |
| 16 | 729 | 8.95 |
| 17 | 794 | 9.33 |
| 18 | 844 | 10.23 |
| 19 | 1010 | 11.77 |
| 20 | 621 | 7.41 |
a. Grafique el diagrama de dispersión.
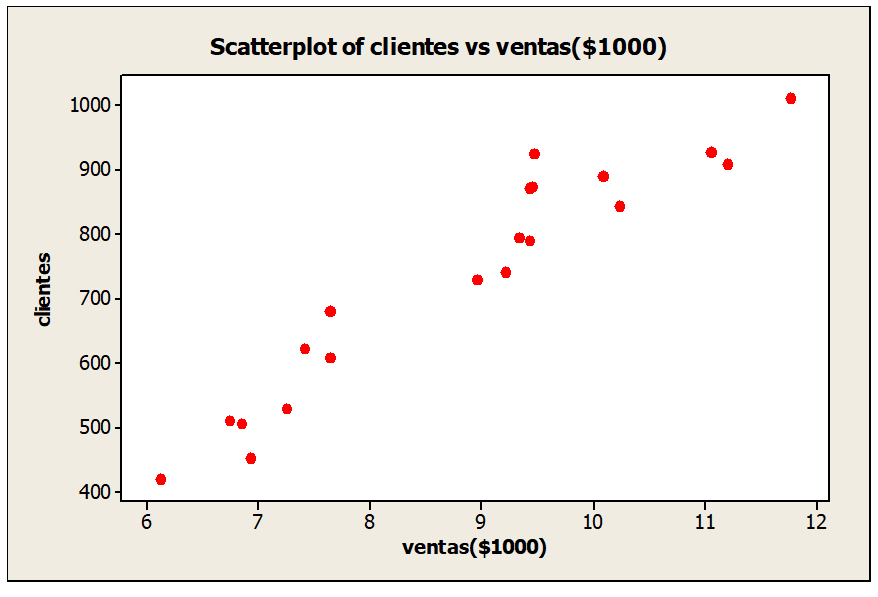
Correlación y regresión lineal – Diagrama de dispersión
b. Obtenga la ecuación que mejor ajuste a los datos.
c. Pronostique las ventas semanales (en miles de dólares) para las tiendas que tienen 600 clientes.
Las ventas serian de algunos 7,500 dólares por como se ve en la tabla la posición de las ventas y de los clientes.
| X | Y | (X-X) | (X-Xi)2 | (Y-Y) | (Y-Y)2 | (X-X)(Y-Y) |
| 907 | 11.2 | 175.85 | 308358.09 | 2.399 | 77.4576 | 421.8641 |
| 926 | 11.05 | 194.85 | 287617.69 | 2.249 | 77.4576 | 192.601 |
| 506 | 6.84 | -225.15 | 906875.29 | -1.961 | 23.8046 | 441.5191 |
| 741 | 9.21 | 9.85 | 520273.69 | 0.409 | 77.4576 | 4.0286 |
| 789 | 9.42 | 57.85 | 453332.89 | 0.619 | 77.4576 | 57.241 |
| 889 | 10.08 | 158.85 | 328672.89 | 1.279 | 77.4576 | 156.571 |
| 874 | 9.45 | 142.85 | 346096.89 | 0.649 | 77.4576 | 142.201 |
| 510 | 6.73 | -221.15 | 906875.29 | -2.071 | 21.7 | 458.0016 |
| 529 | 7.24 | -202.15 | 871048.89 | -1.561 | 32.251 | 315.5561 |
| 420 | 6.12 | -311.15 | 1086389.29 | -2.681 | 11.8267 | 834.1931 |
| 679 | 7.63 | -52.15 | 613558.89 | -1.171 | 41.7186 | 61.0676 |
| 872 | 9.34 | 140.85 | 348454.09 | 0.539 | 77.4576 | 75.9181 |
| 924 | 9.46 | 192.85 | 289766.89 | 0.659 | 77.4576 | 127.0881 |
| 607 | 7.64 | -124.15 | 731538.09 | -1.161 | 41.9774 | 144.1381 |
| 452 | 6.92 | -279.15 | 1020706.09 | -1.881 | 25.3915 | 525.0811 |
| 729 | 8.95 | -2.15 | 537728.89 | 0.149 | 77.4576 | -0.3203 |
| 794 | 9.33 | 62.85 | 446642.89 | 0.529 | 77.4576 | 33.2476 |
| 844 | 10.23 | 112.85 | 382294.89 | 1.429 | 77.4576 | 161.2626 |
| 1010 | 11.77 | 278.85 | 204575.29 | 2.969 | 77.4576 | 827.9056 |
| 621 | 7.41 | -110.15 | 707785.69 | -1.391 | 36.2283 | 153.2186 |
| ?=14623 | ?=176.02 | ?=11298592.6 | ?=1164.3893 | ?=5132.3837 |
Xi= ∑ X/ n
14623/20= 731.15
Yi=∑ Y/ n
176.02/20= 8.801
√ ² Σ(x-xi)2 /n-1
√ ² =11298592.6 /19 = 594662.7684
S=√ 594662.7684= 771.1438
√ ² Σ (y-yi)2/n-1
√ ²=1164.3893 / 19 =61.2836
S= √ 7.8283
Covarianza
Sxy = Σ (xi – x)(yi – y) / n -1
Sxy = 5132.3837 / 19 = 270.1254
Coeficiente de correlación
r = Sxy / SxSy
270.1254/ (771.1438)(7.8283) = 0.0447468
Solución en Minitab de correlación y regresión lineal
Instrucciones para resolver los ejercicios con gráficas, con base en uno de los ejercicios teóricos.
Dar clic en la barra de menú en la opción graph y seleccionar la opción scatterplot.
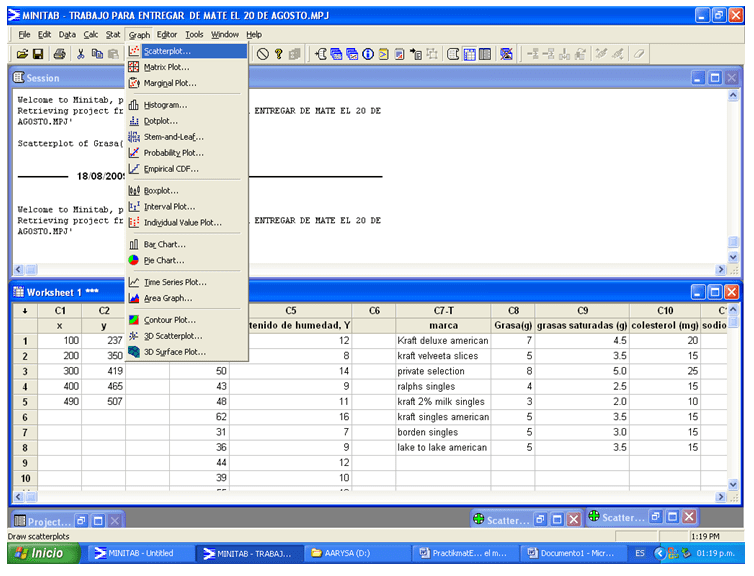
Minitab – Gráfica
Después de haber seleccionado scartterplot, se selecciona la opción simple y se da clic en ok.
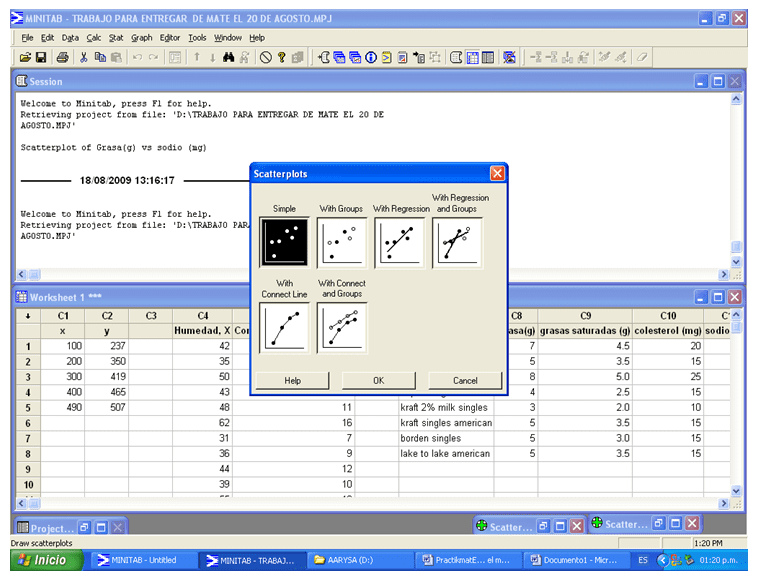
Minitab – Diagrama de dispersión
Después de haber hecho esto aparece esta pequeñísima ventana y se selecciona las variables que se desea utilizar, para después dar clic en ok.
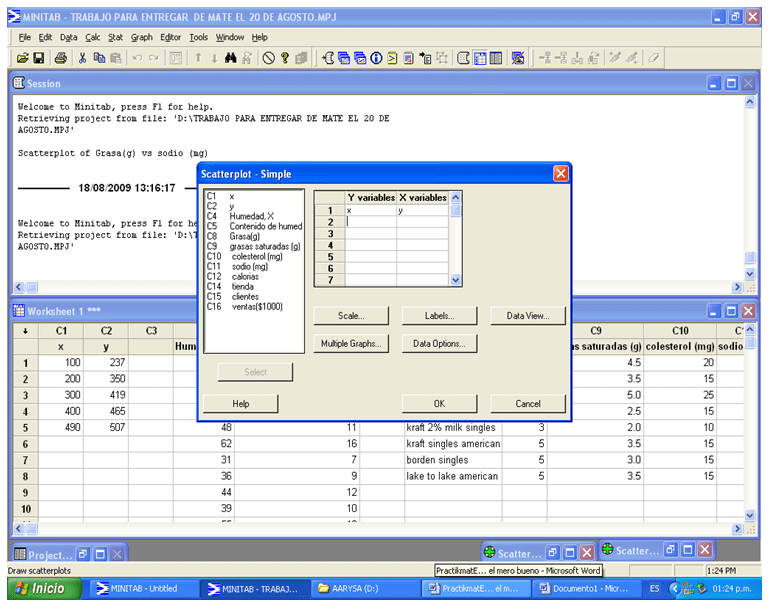
Minitab – Variables
Hecho esto da como resultado la obtención.
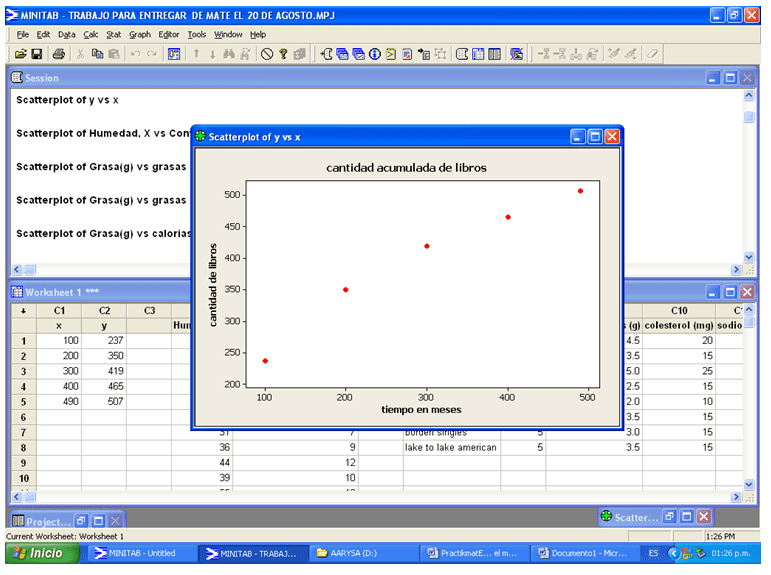
Minitab – Diagrama de dispersión
Conclusiones
Como conclusión nos gustaría decir que esta práctica nos dejó muy en claro que el minitab sirve para hacer grandes cosas y además de ahorrar mucho trabajo es muy fácil utilizarlo para la obtención de diferentes conceptos de estadística como la correlación y algunos diagramas.
Experiencia de aprendizaje
Al estar trabajando en esta práctica aprendimos que con minitab se pueden hacer muchas cosas como los diagramas y obtener la correlación sin el uso de calculadoras y de tantas fórmulas que muchas veces hacen más confuso un problema, además aprendimos a organizarnos como equipo para repartir tareas y así contribuir todos al proyecto, y nos sorprendimos de cómo el minitab puede ahorrar mucho trabajo y que es de mucha ayuda por si en un futuro tendríamos necesidad de utilizarlo.
Bibliografía
- www.wikipedia.com
- Datos proporcionados por el profesor de esta materia.