Según Alan Turing “…si durante el intercambio entre una computadora y el usuario este último cree que está intercambiando con otro humano, entonces se dice que el programa es inteligente…”
La solución de problemas puede considerarse una forma de razonamiento muy compleja que requiere la generación y asimilación de nuevas estructuras de memoria a fin de contestar una interrogante. Es la actividad mental de encontrar una solución a un problema. En el contexto del procesamiento de la información el enfoque dado a la solución de problemas ha sido tratar de trazar la gráfica de la secuencia de eventos desde la formulación del problema hasta su solución final; o sea, tratar de comprender el proceso que interviene para derivar una solución.
Hay cuatro vías principales para encontrar la solución a un problema dado:
- La aplicación de una fórmula explícita que da la solución.
- El uso de una definición recursiva.
- El uso de un algoritmo que converge a la solución.
- La aplicación de otros procesos, en particular la prueba y error.
Siempre que sea posible el primer método es el mejor. Por ejemplo, encontrar los ceros de un polinomio de segundo grado. En este caso la complejidad de hallar la solución es constante, O(1). El método recursivo es computacionalmente muy costoso. Por ejemplo, el cálculo de los números de Fibonacci se formula como:
F(n) = F(n-1) + F(n-2)
F(2) = F(1) = 1
es decir:
procedure F(n);
begin
if n > 2
then F(n):= F(n-1) + F(n-2)
else F(n):= 1
end;
En este caso la complejidad es O[F(n)], quiere decir la complejidad crece exponencialmente. Una alternativa para reducir este costo es transformarlo en un proceso iterativo:
procedure Fibonacci(n);
begin
I := 2; U := 1; V := 1;
while I ¹ n do
begin
I := I + 1;
W := U;
U := U + V;
V := W
end;
return U;
end
Ahora la complejidad es O(n) el lugar de O[F(n)]. Un buen algoritmo puede tener complejidad polinomial.
Las tres primeras vías son las usadas en los programas de computadoras tradicionales; ellos incluyen el desarrollo de un modelo matemático o lógico adecuado que describe un dominio o una parte de él. La solución al problema se deriva del uso de ese modelo. Con la existencia de este modelo se puede hallar una secuencia estructurada de paso que garantiza encontrar una solución al problema en una longitud finita de tiempo. Tales procedimientos son llamados algoritmos y ellos forman la base para sistemas de software convencional.
La cuarta vía es la utilizada para problemas en los cuales no hay una solución algorítmica conocida o es tan compleja que no es posible una implementación computacional conocida práctica. Sin embargo, estos problemas son resueltos por los humanos a pesar de su capacidad de procesamiento “inferior”. Por ejemplo, el problema del Viajero vendedor cae en esta ultima clase de problemas.
Existen problemas combinatorios para los cuales no se conocen algoritmos de resolución que no sean otros que aquellos que producen una explosión del tiempo de cálculo (exponencialmente) al aumentar el tamaño del problema. Por el contrario, para otros problemas combinatorios, como por ejemplo, el denominado problema de asignación consistente en acoplar n trabajadores con n puestos de trabajo sabiendo el costo cij de emparejar el trabajador i con el puesto j, sí existen algoritmos que sólo crecen en tiempo polinomialmente con el tamaño del problema; para el problema de asignación el denominado Algoritmo Húngaro necesita un tiempo de calculo que crece simplemente según n3.
Matemáticamente se trató de caracterizar ambos tipos de problemas. Aquellos para los cuales se conocen algoritmos que necesitan un tiempo polinomial para ofrecer una solución óptima se dice que pertenecen a la clase P y se consideran que son solubles eficientemente. Por otra parte, en la clase NP están incluidos todos los problemas para los que no se conoce un algoritmo de solución polinomial, aunque si sea posible, dada una solución, comprobar en tiempo polinomial si su costo es mejor que un determinado valor. Un ejemplo de problema NP es el problema de la Mochila (seleccionar entre un conjunto de n productos, cada uno con un valor ci y un volumen vi, aquellos que quepan en un recipiente de volumen V y que tengan el mayor valor posible).
De esta clase de problemas es de los que se ocupan los métodos de solución de problemas de la Inteligencia Artificial. La razón está dada por la necesidad de disponer de herramientas que permitan ofrecer soluciones (aunque no sean óptimas) a problemas reales. Esto queda evidenciado claramente en campo empresarial. Los directivos por lo general desean mejorar sus operaciones del modo más rápido, barato y simple posible sin importarles realmente si ése es el modo óptimo. Estos algoritmos, aunque no optimizan una función objetivo, ofrecen soluciones factibles, es decir satisfacen las restricciones del problema, las cuales se acercan al valor óptimo en un tiempo de cálculo razonable. En última instancia puede ser útil encontrar una solución independientemente de su lejanía a una solución óptima.
La inteligencia artificial ofrece técnicas para enfrentar dos clases de problemas:
- Los que por su dimensión hace poco posible usar un algoritmo conocido.
- Los que carecen de algoritmos para resolverlos.
Existe otra definición de inteligencia artificial según Schilt plantea que “…un programa inteligente es el que muestra un comportamiento similar al humano cuando se enfrenta a un problema. No es necesario que el programa resuelva el problema de la misma forma que el hombre…”. Por su parte Forsyth define que “…la inteligencia artificial se relaciona con problemas los cuales han escapado de una caracterización matemática…”.
Un ejemplo es el juego Tic – Tac – Toe:
Estructuras de datos:
Board: Un vector de nueve elementos que se corresponde con las nueve posiciones del tablero. Un elemento que contiene el valor 0 si está vacía la posición, 1 si está ocupado por una X, 2 si está ocupado por una O.
MoveTable: Un vector de 19683 (39), cada elemento del cual es un vector similar a Board.
Algoritmo para jugar:
Para hacer un movimiento, hacer lo siguiente:
- Ver el vector Board como un número ternario (base 3). Convertir este a un número decimal.
- Usar el número computado en el paso anterior como índice a MoveTable y recuperar el vector almacenado allí.
- El vector seleccionado en el paso 2 representa la futura configuración de Board si se hace esa jugada. Hacer la jugada.
Comentarios:
Este programa es muy eficiente en términos de tiempo, y en teoría podrá jugar un juego óptimo. Pero tiene varias desventajas:
- Requiere de mucho espacio para almacenar la tabla que específica el movimiento correcto a hacer desde cada posición.
- Alguien tendrá que hacer un gran trabajo para construir MoveTable.
- Es muy difícil poder construir MoveTable sin errores.
- Si se desea extender el juego, por ejemplo, a tres dimensiones, se tendrá que partir de cero ( si fuera posible almacenar 327 posiciones).
Los investigadores pioneros en I.A. tuvieron como su primer objetivo la solución de problemas que fueron difíciles de resolver mediante las técnicas computacionales existentes. Como se dijo antes, estos problemas generalmente no tienen solución algorítmica conocida o esta es tan compleja que no tiene una implementación práctica computacional.
La respuesta fue desarrollar nuevas técnicas de solución de problemas, similares a las humanas, una de las más importantes fue la búsqueda. La búsqueda de la I.A. difiere de la búsqueda convencional sobre estructuras de datos esencialmente en que se busca en un espacio problema, no en una pieza de dato particular. Se busca un camino que conecte la descripción inicial del problema con una descripción del estado deseado para el problema, es decir, el problema resuelto. Este camino representa los pasos de solución del problema.
El proceso de buscar una solución a un problema produce un espacio solución, o sea, la parte del espacio problema que se examina realmente. A diferencia de las estructuras de datos que están predefinidas y ya existen cuando comienza la búsqueda, los espacios problema son generalmente definidos proceduralmente, es decir, el espacio problema es creado a medida que es explorado. Se usan procedimientos para definir los siguientes estados posibles en el espacio a través de los cuales la búsqueda puede continuar desde el estado actual. Solamente los caminos explorados tienen que estar definidos explícitamente.
En resumen, la búsqueda es el mecanismo de solución de problemas universal en la IA. En los problemas de la IA, la secuencia de pasos requeridos para dar solución a un problema no son conocidos a priori, ellos son determinados mediante la exploración de alternativas.
Hay diferentes alternativas para realizar la búsqueda. Desde un punto de vista podemos apreciar tres alternativas: aleatoria, a ciegas y dirigida. Con el siguiente ejemplo se ilustran estos. Supóngase que está en París sin un mapa y no habla francés ¿Cómo llegar hasta la torre Eiffel?
Un método podía ser tomar aleatoriamente una calle esperando que más pronto que tarde se llegará a la torre. Esta búsqueda aleatoria puede llevar a encontrar la torre pero puede requerir una cantidad infinita de tiempo por la forma arbitraria en la cual seleccionamos un camino (el mismo puede tomarse múltiple veces).
Otra alternativa es seguir exhaustivamente cada calle de inicio a fin. Cuando se alcanza un final se busca una calle paralela y se sigue esta en dirección opuesta independientemente de si nos acercamos o alejamos del objetivo.
Eventualmente esta variante consideraría todas las posiciones de nuestro espacio problema. Este tipo de búsqueda se llama a ciegas, ya que no usa conocimiento de cuan cerca estamos de la solución para tomar un determinado camino.
Alternativamente, podemos usar nuestro conocimiento sobre la torre para mejorar la eficiencia de la búsqueda. Suponiendo que el extremo superior de la torre puede ser visto desde cualquier lugar del espacio problema, podemos tomar la calle que nos parezca nos lleve en esa dirección. Esta es llamada una búsqueda dirigida. La búsqueda dirigida es la base de la I.A.
Otro aspecto a considerar es la dirección de la búsqueda. Puede ser dirigida por dato (forward) o dirigida por objetivo (backward).
Una búsqueda dirigida por dato comienza a partir de la información (o hechos) y trata de extraer conclusiones. Una búsqueda dirigida por objetivo comienza a partir de expectativas de lo que es el objetivo o lo que sucederá, entonces busca las evidencias que soportan o contradicen esas expectativas (o hipótesis).
La selección de la dirección de la búsqueda se determina por las características del problema. Esto incluye la complejidad de las reglas, la forma del espacio de estado y la naturaleza y disponibilidad de los datos del problema.
La búsqueda dirigida por objetivo se recomienda si:
- En el planteamiento del problema se establece un objetivo o hipótesis, o este se puede formular fácilmente.
- Hay una gran cantidad de reglas que se activan con los datos conocidos del problema y por eso se producen una cantidad creciente de conclusiones. Una temprana selección de un objetivo puede eliminar la mayoría de estas ramas.
- Los datos del problema no se dan inicialmente sino que tienen que ser adquiridos por el resolvedor. La búsqueda dirigida por objetivo puede guiar la adquisición de datos.
La búsqueda dirigida por dato es apropiada para problemas en los cuales:
- Todos o la mayoría de los datos se conocen en el estado inicial.
- Hay una gran cantidad de objetivos potenciales.
- Es difícil formular el objetivo o la hipótesis.
Los problemas que caen en el campo de la IA caen en tres clases generales: problemas de encontrar el camino de un simple agente, juegos entre dos contrarios, y problemas de satisfacción de restricciones. Ejemplos clásicos de la primera clase es el juego de las 8 fichas, problema del viajero vendedor, y el de wiring of VLSI circuits, en todos los casos la tarea es encontrar la secuencia de operaciones que lleva un estado inicial a uno final. La segunda clase de problemas incluye los juegos con información perfecta entre dos jugadores (mas recientemente se han desarrollado algoritmos de búsqueda para juegos con información imperfecta) tales como el ajedrez y las damas. En la categoría de problemas de satisfacción de restricciones corresponde a problemas como el juego de las 8 reinas y problemas de planificación.
Considérese un agente quien actúa como resolvedor de problemas. Un problema es realmente una colección de información que el agente usará para decidir qué hacer.
Los elementos básicos de la definición de un problema son los estados y las acciones. Los elementos son los siguientes:
El estado inicial donde se encuentra el agente.
El conjunto de acciones posibles disponibles al agente. El término operador se usa para denotar la descripción de una acción en términos de cual estado será alcanzado ejecutando la acción en un estado particular. Una formulación alternativa es usar una función sucesor S; dado un estado particular x, S(x) retorna al conjunto de estados alcanzables desde x mediante una acción simple.
El espacio de estado del problema es el conjunto de todos los estados alcanzables a partir del estado inicial mediante una secuencia de acciones cualquiera.
Un camino en el espacio de estado es una secuencia de acciones que conduce de un estado a otro.
El criterio objetivo es el criterio que el agente usa para aplicarlo a la descripción de un estado para determinar si este es un estado objetivo (lo que se desea obtener). Algunas veces hay un conjunto explícito de posibles objetivos y el criterio simplemente consiste en chequear si se ha alcanzado uno de ellos. Otra variante es especificar el objetivo por una propiedad abstracta, por ejemplo, el criterio de jaque mate del ajedrez.
El costo de un camino es una función que asigna un costo a un camino.
Una solución es un camino desde el estado inicial a un estado que satisface el criterio objetivo.
Otro concepto importante es el de costo de la búsqueda asociado con el tiempo y la memoria requisitos para encontrar una solución.
El costo total de la búsqueda es la suma del costo del camino y el costo de la búsqueda.
Ejemplo:
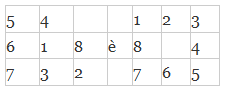
El rompecabezas de 8 piezas (8 – puzzle).
Consiste en un tablero de 9 casillas (3×3), en 8 de ellas se colocan fichas numeradas del 1 al 8 y una queda en blanco. El juego consiste en alcanzar una posición dada del tablero usando como regla que solo se puede mover una ficha a una casilla adyacente que este vacía. La esencia del rompecabezas es dada cualquier numeración de las casillas obtener una con un orden específico, por ejemplo:
Planteamiento de un problema de las 8 fichas.
La formulación del problema es:
Estados: La descripción de un estado especifica la localización de cada ficha y la del espacio en blanco.
Operadores: una ficha se mueve a la izquierda, derecha, arriba o abajo.
Criterio objetivo: Los 8 números quedan en un orden especificado.
Costo del camino: Cada paso cuesta una unidad.
Este problema a pesar de parecer simple tiene 9! = 36280 diferentes ordenamientos de los números en blanco, por lo que el método de simplemente generar estados y probar si cumplen el criterio objetivo lleva a una explosión combinatorial.
Dada la formulación de un problema la próxima acción es encontrar una solución, lo cual como ya se vio consiste en generar nuevos estados a partir del estado donde se encuentra el agente. El proceso consiste en generar nuevos estados a partir del estado donde se encuentra el agente. Este proceso se denomina expandir el estado. La expansión puede producir uno o varios nuevos estados. En el primer caso se toma este y se continúa, en el otro caso existen múltiples posibilidades para continuar la búsqueda por lo que es necesaria una selección.
Esta es la esencia de la búsqueda, seleccionar una opción y poner las otras alternativas a un lado para retomarla más tarde si la primera selección no conduce a una solución. La selección de cuál estado expandir primero se determina por la estrategia de búsqueda.
La búsqueda consiste en ir construyendo un espacio de búsqueda (la parte del espacio de estado que deja de ser abstracta). La raíz del espacio de búsqueda se corresponde con el estado inicial. Aunque la mayoría de los espacios de búsqueda se corresponden con grafos con más de un camino entre un par de nodos, por simplicidad ellos son frecuentemente representados como árboles, donde el estado inicial es la raíz del árbol. El costo de esta simplificación es que cualquier estado que pueda ser alcanzado por dos caminos diferentes se representará por nodos duplicados, incrementando el tamaño del árbol. El beneficio del árbol es que la ausencia de ciclos simplifica grandemente muchos algoritmos de búsqueda.
Los nodos hojas del árbol corresponden a estados que no tienen sucesores en el árbol porque no han sido expandidos o porque no tienen sucesores. En cada paso el algoritmo de búsqueda selecciona un nodo hoja a expandir.
El tamaño de un problema de IA raramente se expresa en términos de la cantidad de nodos de su espacio problema, sino mediante dos parámetros que caracterizan el árbol de búsqueda, los cuales caracterizan la eficiencia de los algoritmos de búsqueda. Estos son el factor de ramificación y la profundidad de la solución. El factor de ramificación es el número promedio de hijos de un nodo dado; por ejemplo, en el juego de las ocho fichas este factor es raíz cuadrada de 3. La profundidad de la solución de una instancia de un problema es la longitud del camino mas corto desde el estado inicial al estado objetivo, o la longitud de la secuencia mas corta de operadores que resuelve el problema.
Debe distinguirse entre el espacio de estado y el espacio de búsqueda. Por ejemplo en el problema del viajero vendedor (considerando 20 ciudades) hay solamente 20 estados en el espacio de estado, uno por cada ciudad. Pero hay un número grande de caminos en el espacio de estado de modo que había una gran cantidad de nodos en el espacio de búsqueda.
Algoritmo de búsqueda general:
function General_Search(Problem, Strategy) return Solucion;
Inicializar el árbol de búsqueda usando el estado inicial o Fallar
Loop do
if no hay nodo que expandir then return Falla
Seleccionar un nodo hoja a expandir de acuerdo a la estrategia.
if el nodo contiene un estado objetivo
then return Solucion
else expandir el nodo y añadir los nodos resultantes al
espacio de búsqueda.
end loop.
end
La estrategia de búsqueda define el criterio para seleccionar el siguiente nodo a expandir. La estrategia se avalúa atendiendo a cuatro aspectos:
- Completitud: ¿Garantiza la estrategia encontrar una solución cuando esta exista?
- Complejidad del tiempo: ¿Cuánto tiempo requiere encontrar una solución?
- Complejidad del espacio: ¿Cuánta memoria se necesita para realizar la búsqueda?
- Optimalidad: ¿Encuentra la estrategia la solución de mayor calidad cuando haya varias soluciones diferentes?
En la búsqueda exhaustiva la idea es examinar el espacio de estado completamente de una manera ordenada, usando todos los operadores y generando todos los sucesores posibles para encontrar la solución deseada.
La búsqueda a ciegas es aquella donde no existe ninguna información para decidir que nodo expandir, no se conoce la cantidad de pasos o el costo del camino desde el estado actual hasta el objetivo. También se denomina búsqueda no informada. En el otro caso, cuando existe información para decidir, la búsqueda se denomina informada o heurística.
El conjunto de métodos que utilizan la estrategia de búsqueda a ciegas se consideran métodos débiles pues imponen restricciones mínimas a la búsqueda y su alta generalidad implica cierta debilidad. Los métodos con estrategia informada se llaman métodos fuertes, ellos son más dependientes del dominio.
Los dos métodos básicos de la búsqueda a ciegas son la búsqueda primero a lo ancho (breadth-first search) y la búsqueda primero en profundidad (depth-first search). Las estrategias y las direcciones de la búsqueda se pueden combinar pues la estrategia define que nodo generar y la dirección determina que contiene cada nodo. En la búsqueda dirigida por datos los nodos contienen los hechos dados como datos iniciales y los que se van infiriendo, mientras en la búsqueda dirigida por objetivos los nodos contienen los objetivos y subobjetivos.
La idea principal es realizar simultáneamente dos búsquedas, una dirigida por dato y otra por objetivo y parar cuando ambas se encuentren. Entonces el camino desde el estado inicial se concatena con el inverso del camino desde el estado objetivo para formar el camino solución.
La complejidad en tiempo y espacio de esta búsqueda es O(bd/2). La búsqueda bidireccional puede reducir enormemente la complejidad en tiempo (para b=10 y d=6 una búsqueda primero a lo ancho genera 1 111 111 nodos mientras que la bidireccional 2222), pero no siempre es aplicable. Sus requerimientos de memoria pueden ser altos y exige operadores inversibles.
Bibliografía
Rafael Bello, Presentación Power Point, Inteligencia Artificial, Universidad Central de Las Villas, Cuba, Abril 2005.
Rafael Bello, Métodos de Solución de Problemas de la Inteligencia Artificial, Universidad Central de Las Villas, 2007.
Ivan Bratko, Prolog programming for Artificial Intelligence. Addison-Wesley Publishing Company, Reading, Mass., 1986.