Este artículo está vinculado a la investigación realizada dentro de un Proyecto de Tesis Doctoral relacionado con la calidad del servicio de Auditoría. Se hace necesaria la selección de territorios para realizar las investigaciones, cuya selección no debe ser un fenómeno al azar, sino el resultado de un proceso donde se utilizan herramientas estadísticas que lo justifiquen, para ellos se utiliza la técnica de Análisis de Clúster, relacionándose este a las variables definidas basadas en el servicio de Auditoría.
Introducción al análisis de Clúster.
El análisis de Clúster, también conocido como Análisis de Conglomerados, Taxonomía Numérica o Reconocimiento de patrones, es una técnica estadística multivariante cuya finalidad es dividir un conjunto de objetivos en grupos, de forma que los perfiles de los objetivos en un mismo grupo sean muy similares entre sí (cohesión interna del grupo) y los de los objetivos de clústers diferentes sean distintos (aislamiento externo del grupo).
Académicos e investigadores de mercado a menudo encuentran la mejor solución para resolver sus estudios mediante la definición de grupos homogéneos de objetos, ya sean ellos individuos, firmas, productos, o incluso comportamientos.
Opciones estratégicas basadas en la identificación de grupos dentro de la población tales como la segmentación o el marketing de objetivos no serían posibles sin un objetivo metodológico. La misma necesidad nos la encontramos en otras áreas, abarcando desde las ciencias físicas (por ejemplo, clasificación de varios grupos de animales, como insectos o mamíferos) a las ciencias sociales (por ejemplo, análisis de varios perfiles psiquiátricos).
En todos estos ejemplos, el analista trata de encontrar una estructura natural a través de las observaciones basándose en un perfil multivariado. La técnica más comúnmente usada para este propósito es el Análisis de Conglomerados (Análisis Clúster, AC, desde ahora).
Conviene tener claro desde el principio:
- Que la técnica no tiene vocación / propiedades inferenciales
- Que por tanto, los resultados logrados para una muestra sirven sólo para ese diseño (su valor atañe sólo a los objetivos del analista): elección de individuos, variables relevantes utilizadas, criterio similitud utilizado, nivel de agrupación final elegido…. definen diferentes soluciones.
- Que Clúster y discriminante no tiene demasiado en común: el discriminante intenta explicar una estructura y el Clúster intenta determinarla.
Dos Objetivos Básicos:
- Análisis «taxonómico» con fines exploratorios o confirmatorios.
- Cambio (simplificación) de la dimensión de los datos (lo descrito al inicio de este documento: agrupación de objetos individuales en nuevas estructuras de estudio (grupales))
¿Qué es el Análisis de Conglomerados?
El AC no es más que un conjunto de técnicas que se utilizan para clasificar los objetos o casos en grupos relativamente homogéneos llamados conglomerados (Clústers).
Los objetos en cada grupo (conglomerados) tienden a ser similares entre sí (alta homogeneidad interna, dentro del Clúster) y diferentes a los objetos de los otros grupos (alta heterogeneidad externa, ente Clúster) con respecto a algún criterio de selección predeterminado.
De este modo, si la clasificación es un éxito, los objetos dentro del clúster estarán muy cercanos unos de otros en la representación geométrica, y los clúster diferentes estarán muy apartados. Este análisis se conoce también como análisis de clasificación o taxonomía numérica.
El AC tiene como propósito esencial, agrupar aquellos objetos que reúnan idénticas características, es decir, se convierte así en una técnica de análisis exploratorio diseñada para revelar las agrupaciones naturales dentro de una colección de datos. Este análisis no hace ninguna distinción entre variables dependientes (VD) y variables independientes (VI) sino que calcula las relaciones interdependientes de todo el conjunto de variables.
El AC se utiliza en mercadotecnia para diversos propósitos, entre los que se encuentran:
- Segmentación del mercado
Por ejemplo, los consumidores pueden agruparse empleando como base los beneficios derivados de la compra de un producto. Cada grupo consistirá en consumidores relativamente homogéneos en términos de los beneficios que buscan. Este planteamiento se conoce como segmentación de los beneficios. - Comprensión del comportamiento del comprador
El AC puede utilizarse para identificar grupos de compradores homogéneos. Así, el comportamiento de cada grupo puede estudiarse por separado. Este análisis también se utiliza para identificar la clase de estrategias que los compradores emplean para obtener información externa. - Identificación de oportunidades para productos nuevos
Al agrupar marcas y productos, pueden determinarse los conjuntos competitivos dentro del mercado. Las marcas en el mismo grupo compiten más entre sí que con las de los otros grupos. Una empresa puede analizar sus ofertas actuales en comparación con aquéllas de sus competidores a fin de identificar las oportunidades potenciales de los nuevos productos. - Selección de mercados de prueba
Al dividir las ciudades en grupos homogéneos, es posible seleccionar ciudades comparables a fin de probar diversas estrategias de mercadotecnia. - Reducción de datos
El AC puede utilizarse como instrumento de reducción general de datos a fin de desarrollar subgrupos de datos que sean más fáciles de manejar que las observaciones individuales. El análisis multivariante subsecuente se realiza con base en los subgrupos, en lugar de las observaciones individuales. Por ejemplo, para describir las diferencias en el comportamiento de uso del producto, primero pueden agruparse los consumidores. Las diferencias entre los conglomerados pueden estudiarse con el uso del análisis discriminante múltiple.
El AC es una herramienta útil a la hora de analizar datos en muy diversas situaciones. Por ejemplo, un investigador que está recogiendo datos por medio de un cuestionario podría encontrarse con un gran número de observaciones que no tienen significado a menos que se encuentren dentro de grupos manejables.
El AC puede llevar a cabo esta agrupación de datos de manera objetiva reduciendo la información de una población entera o la muestra de información sobre pequeños grupos específicos. Por ejemplo, si nosotros podemos entender las actitudes de una población identificando los grupos de mayor tamaño dentro de la población, entonces podemos reducir los datos de una población entera dentro de un numeroso número de grupos. De esta forma el investigador logra una mayor concisión y una descripción más comprensible de las observaciones, con una mínima pérdida de información.
El AC puede usarse también cuando un investigador desea desarrollar hipótesis concernientes a la naturaleza de los datos. Por ejemplo, un investigador podría creerse las actitudes sobre la consumición de refrescos bajos en azúcar frente a los consumidores de refrescos normales podrían ser usados para separar a los consumidores en grupos o segmentos lógicos. El AC puede clasificar a los consumidores de refrescos por las actitudes que adoptan frente a refrescos normales o frente a refrescos bajo en calorías, y los clústers resultantes pueden perfilarse a partir de las similaridades y de las diferencias demográficas.
Con todo, no debe esperarse nunca una única y definitiva solución al problema de creación de conglomerados.
En la práctica, se considerarán varias soluciones derivadas de la aplicación de las muchas técnicas ofrecidas por este análisis y, tras su correspondiente comparación, nos inclinaremos por la más útil para el tipo de investigación planteada. Los conocimientos del investigador sobre sus clientes, productos o servicios, jugarán un papel importante a la hora de decidir entre las diferentes soluciones alternativas.
Conceptos básicos del Análisis Clúster
La mayoría de los procedimientos utilizados en esta técnica multivariante son relativamente sencillos, ya que no están respaldados por el razonamiento estadístico. La mayor parte de los métodos de agrupación son heurísticos, basados en algoritmos. De este modo, el AC presenta un fuerte contraste con el análisis de la varianza, la regresión, el análisis discriminante y el análisis factorial, que se basan en un razonamiento estadístico.
Los principios fundamentales implicados en cualquier AC son:
- Informe de Aglomeración
Ofrece información sobre los objetos o casos que se combinan en cada etapa de un proceso de agrupación jerárquica. - Centroides de Agrupamiento
Son los valores medios (medias) de las variables para todos los casos u objetos de un grupo particular. - Centros de Agrupamiento
Son los puntos de partida iniciales en la agrupación no jerárquica. Los grupos se construyen alrededor de estos centros o semillas. - Participación en el Grupo
Indica el grupo al que pertenece cada objeto o caso. - Dendrograma
Llamado también gráfica de árbol, es un dispositivo gráfico para presentar los resultados del conglomerado.
Las líneas verticales representan los grupos que están unidos. La posición de la línea en la escala indica las distancias en las que se unieron los grupos. Se lee de izquierda a derecha. - Distancias entre Centros de Grupos
Indican la separación existente entre los pares individuales de los grupos. Los grupos muy separados son distintos y, por tanto, deseables. - Diagrama de Carámbanos
Es una representación gráfica de los resultados del conglomerado, se llama así porque se asemeja a una hilera de carámbanos que pende del alero de una casa. Las columnas corresponden a los objetos que se agrupan y los renglones corresponden al número de conglomerados. Se lee de abajo hacia arriba. - Matriz de Coeficientes de Distancia/Similitud
Es una matriz de triángulo inferior que contiene las distancias en dirección pareada entre los objetos o casos.
Pasos del Análisis de Conglomerados
 El primer paso consiste en formular el problema de agrupación al definir las variables en las que se basa ésta. Después, debe seleccionarse una medida de distancia apropiada. La medida de distancia determina cómo de similares o diferentes son los objetos que se agrupan. Posteriormente, debe seleccionarse un procedimiento de agrupación. Se dispone de varios, pero es labor del investigador elegir aquél que mejor se ajuste al problema de investigación propuesto.
El primer paso consiste en formular el problema de agrupación al definir las variables en las que se basa ésta. Después, debe seleccionarse una medida de distancia apropiada. La medida de distancia determina cómo de similares o diferentes son los objetos que se agrupan. Posteriormente, debe seleccionarse un procedimiento de agrupación. Se dispone de varios, pero es labor del investigador elegir aquél que mejor se ajuste al problema de investigación propuesto.
La decisión del número de conglomerados requiere del criterio del investigador. Los conglomerados obtenidos deben interpretarse en términos de las variables sobresalientes adicionales. Por último, es preciso que el investigador evalúe la validez del proceso de conglomerados.
1. Formulación del Problema
Quizá la parte más importante de la formulación del problema del AC sea la selección de las variables en las que se basa la agrupación. La inclusión de una o más variables irrelevantes puede distorsionar una solución de agrupación que de otra forma podría ser útil. Básicamente, el conjunto de variables seleccionado debe describir la similitud entre los objetos en términos relevantes para el problema de investigación de mercados. Las variables deben seleccionarse con base en la investigación previa, la teoría o una consideración de las hipótesis que se prueban. En la investigación exploratoria, el investigador debe poner en práctica el criterio y la intuición.
2. Selección de una Medida de Similitud
Ya que el objeto del conglomerado es agrupar objetos similares, se necesita alguna medida para evaluar las diferencias y similitudes entre objetos. El concepto de similaridad es fundamental en el Análisis Clúster. La similaridad (similitud) es una medida de correspondencia o semejanza entre los objetos que van a ser agrupados. La estrategia más común consiste en medir la equivalencia en términos de la distancia entre los pares de objetos. Los objetos con distancias reducidas entre ellos son más parecidos entre sí que aquellos que tienen distancias mayores y se agruparán, por tanto, dentro del mismo clúster.
De esta manera, cualquier objeto puede compararse con cualquier otro objeto a través de la medida de similaridad.
En la medición de la similitud entre los objetos de un AC existen tres métodos:
- Medidas de Correlación
- Medidas de Distancia
- Medidas de Asociación
Cada uno de estos métodos representa una particular perspectiva de la similitud, dependiendo tanto de los objetivos como del tipo de datos. Las medidas de correlación y las de distancia requieren datos métricos, mientras que las medidas de asociación requieren datos no métricos.
Muchos programas informáticos han limitado la ayuda para las medidas de asociación, y el investigador se ve forzado con frecuencia a calcular primero las medidas de similaridad y después a introducir la matriz de similaridad dentro de un programa clúster.
3. Estandarización de Datos
Una vez seleccionada la medida para cuantificar la similaridad entre pares de objetos, el investigador debe plantearse una última cuestión… ¿deben estandarizarse los datos antes de calcular las similaridades?. Para poder responder a esta pregunta de forma adecuada, el investigador debe tener en cuenta que la mayoría de las medidas de distancia son bastante sensibles a las diferencias de escalas o de magnitudes hechas entre las variables.
En general, las variables con una gran dispersión (valores grandes de sus desviaciones típicas) tienen más impacto en el valor final de la similaridad.
Consideremos como ejemplo que se quieren agrupar las individualidades de una serie de personas en tres variables, que son: actitud frente a un producto, edad e ingresos. Se supone que medimos la actitud en una escala de siete puntos de gusto-disgusto, mientras que la edad se medía en años y los ingresos en dólares.
Si representamos los resultados obtenidos de la pertinente encuesta en un gráfico tridimensional, la distancia entre los puntos (y sus similaridades) estarían basadas casi totalmente en las diferencias de ingresos.
La explicación es bien sencilla, mientras que las posibles diferencias de actitud frente al producto se encuentran en un rango de actitudes que va de uno a siete, las producidas en los ingresos pueden tener un rango cien veces mayor.
De este modo, no seríamos capaces (gráficamente) de observar ninguna diferencia en la dimensión asociada a la actitud frente al producto. Por este motivo, el investigador debe ser consciente del peso implícito de las variables que participan en el estudio de investigación.
La forma más común de estandarización es la conversión de cada variable en puntuaciones típicas (también conocidas como puntuaciones Z). La forma de cálculo es que se resta a cada observación de cada variable su media correspondiente y se divide el resultado de esta operación por la desviación típica (estándar) de la variable en cuestión.
Este proceso convierte la puntuación de cada dato original en un valor estandarizado con una media de cero y una desviación típica de uno. En definitiva, lo que se consigue con ello es eliminar, uno por uno, los prejuicios introducidos por las diferencias en las escalas de los distintos atributos (variables) usados en el análisis.
4. Supuestos del Análisis
El AC es un objetivo metodológico para cuantificar las características de un conjunto de observaciones. Por ello, tiene fuertes propiedades matemáticas, pero no fundamentos estadísticos. Los requisitos de normalidad, linealidad y homocedasticidad (tan relevantes en otras técnicas), tienen poca consistencia en el AC.
El investigador debe, sin embargo, centrar su atención en otras dos cuestiones esenciales para este tipo de análisis, como son: la representatividad de la muestra y la multicolinealidad.
En muchas ocasiones se dispone de un censo de población para hacer uso del análisis clúster. Se obtiene entonces una muestra de casos y se espera que los clúster obtenidos de ella sean representativos de la estructura de la población original. El analista debe tener siempre presente que el análisis clúster será tan bueno como lo sea la representatividad de la muestra.
Así, todos los esfuerzos deben centrarse en asegurar esa representatividad, para que los resultados puedan ser generalizables a la población de interés.
La multicolinealidad era un resultado en otras técnicas multivariantes, ya que se hacía difícil diferenciar el verdadero impacto de las variables multicolineales. En el análisis clúster, en cambio, el efecto es diferente, ya que las variables multicolineales están ponderadas, implícitamente, de un modo más severo.
Supongamos, por ejemplo, que se agrupan a los encuestados en diez variables relacionadas con un determinado servicio. Al examinar la multicolinealidad, apreciamos que realmente hay dos grupos de variables claramente diferenciados.
El primero está compuesto por ocho elementos (variables) y el segundo de los dos restantes.
Si lo que pretendemos es agrupar realmente a los encuestados en las dimensiones del servicio analizado (en este caso representado por los dos grupos de variables), no podremos considerar a las diez variables como un todo, ya que eso significaría ponderar equitativamente cada variable.
Es decir, al ponderar el análisis clúster uniformemente cada variable, la primera dimensión tendría cuatro veces más oportunidades (ocho ítems frente a dos) de afectar a la medida de similaridad de las que tendría la segunda dimensión.
Así, el acto de la multicolinealidad es un proceso de ponderación oculto al observador, pero que afecta, sin embargo, al análisis. Por esta razón, el analista debe fomentar el estudio exhaustivo de las variables utilizadas en el análisis clúster para poder hallar así la posible multicolinealidad.
Si se encuentra multicolinealidad en las variables empleadas para el estudio, habrá que conseguir igual número de ellas en cada conjunto o usar una de las medidas de distancia, como la Distancia de Mahalanobis, para compensar la correlación existente descubierta.
Una vez seleccionadas las variables y calculada la matriz de similaridades, comienza el proceso de partición. Primeramente el investigador debe seleccionar el algoritmo de agrupación que se va a emplear para formar los clústers (grupos) y posteriormente tomar la decisión sobre el número de grupos que se quieren formar.
Ambas decisiones tienen substanciales implicaciones no solamente en los resultados que se obtengan, sino también en la interpretación que pudiera derivarse de ellos.
5. Selección del Procedimiento de Agrupación
Hay dos tipos de procedimientos: los jerárquicos y los no jerárquicos. El conglomerado jerárquico se caracteriza por el desarrollo de una jerarquía o estructura en forma de árbol.
Una característica importante de los procedimientos jerárquicos es que los resultados de la primera etapa pueden estar anidados con los resultados de la última etapa, dando lugar a una similaridad parecida a la de un árbol. Por ejemplo, la solución del clúster seis se obtienen gracias a la unión de dos de los clústers encontrados en la fase siete del clúster.
De este modo, los clústers están formados solamente por la unión de los grupos existentes, así cualquier miembro de un clúster puede trazar su relación en un irrompible sendero que comenzaría con una simple relación.
Los métodos jerárquicos pueden ser por Aglomeración o por División. El conglomerado por aglomeración empieza con cada objeto en un grupo separado.
Los conglomerados se forman al agrupar los objetos en conjuntos cada vez más grandes. Este proceso continúa hasta que todos los objetos formen parte de un solo grupo.
El conglomerado por división comienza con todos los objetos agrupados en un solo conjunto. Los conglomerados se dividen hasta que cada objeto sea un grupo independiente.
Dentro de los conglomerados por aglomeración, se encuentran los métodos de conglomerados, que se utilizan con frecuencia en la investigación de mercados.
Consisten en métodos de Enlace, métodos de Varianza o de sumas de los cuadrados del error y el método Centroide. Los Métodos de Enlace incluyen el enlace sencillo, el completo y el promedio.
El método de enlace sencillo se basa en la distancia mínima o la regla del vecino más próximo. Los primeros dos objetos conglomerados son aquellos que tienen la menor distancia entre sí. La siguiente distancia más corta se identifica, ya sea que el tercer objeto se agrupe con los dos primeros o que se forme un nuevo conglomerado de dos objetos.
En cada etapa, la distancia entre dos conglomerados es la distancia entre sus dos puntos más próximos.
En cualquier etapa, dos conglomerados surgen por el enlace sencillo más corto entre éstos. Este proceso continúa hasta que todos los objetos se encuentren en un conglomerado.
El método del enlace sencillo no funciona adecuadamente cuando los conglomerados no están bien definidos.
El método del enlace completo es similar al enlace sencillo, excepto que se basa en la distancia máxima o la estrategia del vecino más lejano. En este caso, la distancia entre dos conglomerados se calcula como la distancia entre sus puntos más lejanos.
El método del enlace promedio funciona de manera similar, pero en este método, la distancia entre dos conglomerados se define como el promedio de las distancias entre todos los pares de objetos, donde se encuentra un miembro del par de cada uno de los conglomerados (Véase Figura Métodos de Enlace para el Conglomerado). Como puede apreciarse, el método del enlace promedio emplea la información sobre todos los pares de distancias, no sólo las mínimas o máximas. Por esta razón, generalmente se prefiere a los métodos de enlace sencillo y completo.
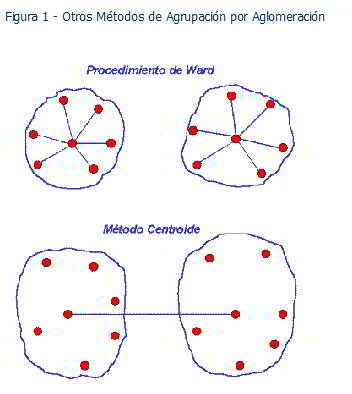
Los Métodos de Varianza tratan de generar conglomerados a fin de reducir la varianza dentro de los grupos. Un método de la varianza que se utiliza con frecuencia es el Procedimiento de Ward.
Para cada conglomerado, se calculan las medias para todas las variables. Después, para cada objeto, se calcula la distancia euclidiana cuadrada para las medias de los grupos (Figura Otros métodos de Agrupación por Aglomeración); estas distancias se suman a todos los objetos. En cada etapa, se combinan los dos conglomerados con el menor incremento en la suma total de los cuadrados de las distancias dentro de los conglomerados.
En el Método Centroide, la distancia entre dos grupos es la distancia entre sus centroides (medias para todas las variables), como se muestra en la Figura Otros métodos de Agrupación por Aglomeración.
Cada vez que se agrupan los objetos, se calcula un centroide nuevo. De los métodos jerárquicos, el método de Enlace Promedio y el Procedimiento de Ward han demostrado un mejor desempeño que los otros.
El segundo tipo de procedimientos de conglomerados, los métodos de conglomerados no jerárquicos, con frecuencia se conocen como Agrupación de K Medias.
Estos métodos incluyen el Umbral Secuencial, Umbral Paralelo y la División para la Optimización.
En el método del Umbral Secuencial, se selecciona un centro de grupo y se agrupan todos los objetos dentro de un valor de umbral que se especifica previamente a partir del centro.
Después, se selecciona un nuevo centro o semilla de grupo y el proceso se repite para los puntos sin agrupar. Una vez que un objeto se agrupa con una semilla, ya no se considera para su conglomerado con semillas subsecuentes. El método del Umbral Paralelo funciona de manera similar, excepto que se seleccionan simultáneamente varios centros de grupo y se agrupan los objetos del nivel del umbral dentro del centro más próximo.
El método de División para la Optimización difiere de los otros dos procedimientos de umbral en que los objetos pueden reasignarse posteriormente a otros grupos, a fin de optimizar un criterio general, como la distancia promedio dentro de los grupos para un número determinado de conglomerados.
Existen dos formas básicas de conocer el modo de agrupación de los objetos en cuestión:
- Gráfico de Carámbanos
Sus columnas corresponden a los objetos que se agrupan (entrevistados,…) y las filas al número de grupos. Esta figura se lee de abajo hacia arriba. Inicialmente todos los casos se consideran como grupos individuales. En el primer caso, se combinan los dos objetos más cercanos.
Cada paso subsecuente lleva a la formación de un nuevo grupo en una de las siguientes tres formas: (1) se agrupan dos casos individuales, (2) un caso se une a un grupo ya existente, (3) se unen dos grupos. - Dendrograma
Se lee de izquierda a derecha. Las líneas verticales representan los grupos unidos. La posición de la línea en la escala indica las distancias en las que se unen los grupos.
Debido a que, en las primeras etapas, muchas distancias tienen magnitudes similares, es difícil determinar la secuencia en la que se forman algunos de los primeros conglomerados. Sin embargo, es evidente que en las últimas dos etapas, las distancias en las que se combinan los conglomerados son grandes. Esta información es útil para decidir el número de conglomerados.
También es posible obtener información sobre la participación de los conglomerados de los casos si se especifica el número de grupos. Aun cuando esta información puede deducirse del trazo de carámbano, resulta útil una representación tabular.
Métodos Jerárquicos y No Jerárquicos
6. Decisión del Número de Conglomerados
Un gran problema en todas las técnicas de aglomeración es cómo seleccionar el número de grupos (clústers). Desgraciadamente, no existe un proceso objetivo de selección.
Para el caso del análisis clúster jerárquico, las distancias existentes entre los clústers reflejadas en las distintas etapas del proceso de aglomeración pueden servirnos de guía útil, el analista podría así establecer un tope para detener el proceso a su conveniencia (esta información puede obtenerse del programa de aglomeración o del dendrograma).
Por ejemplo, podría hacerlo cuando la distancia entre los grupos exceda un valor específico o cuando las distancias sucesivas entre los pasos marquen un repentino salto.
Sin embargo, la opción más utilizada es calcular distintas soluciones de aglomeración (dos, tres, cuatro grupos, por ejemplo) para después decidir entre las soluciones alternativas con ayuda de un criterio prefijado de antemano, del sentido común, o de fundamentos teóricos.
Estas distancias reciben a menudo el nombre de medidas de variabilidad del error.
Para el caso del análisis clúster no jerárquico, se puede trazar un gráfico que compare el número de grupos con la relación entre la varianza total de los grupos y la varianza entre los grupos.
El punto del gráfico donde se presente un recodo o doblez marcado indicará el número apropiado de grupos. Por lo general, no merecerá la pena aumentar el número de grupos más allá de este punto. Otra posibilidad para decidir el número óptimo de grupos es definir algún tipo de conceptualización intuitiva de la relación teórica de los datos.
Los investigadores deben examinar la variación producida entre los tamaños de los grupos desde una perspectiva conceptual, comparando los resultados obtenidos con las expectativas creadas en los objetivos del estudio.
Otro problema que puede presentarse en este tipo de análisis es la presencia de grupos unipersonales, es decir, clústers formados por un solo individuo. Son un problema porque podrían ser outliers (valores atípicos) no detectados en el proceso de depuración de nuestra fuente de datos.
Si aparece un grupo de un solo miembro, el analista debe estudiar si representa un componente estructural válido en la muestra o si, por el contrario, debiera suprimirse por no ser representativo. Si se suprime del análisis alguna observación, el investigador deberá ejecutar de nuevo el análisis clúster para las nuevas observaciones válidas y conseguir así definir nuevos grupos.
7. Interpretación y Elaboración del Perfil de los Clúster
La interpretación y el perfil de los grupos comprende el análisis de los centroides de grupo. Los centroides representan los valores medios de los objetos que contiene el grupo en cada una de las variables. Los centroides nos permiten describir cada grupo al asignarle un nombre o etiqueta.
Si el programa de conglomerado no ofrece esta información, puede obtenerse por medio del análisis discriminante.
El objetivo de esta etapa es, esencialmente, examinar la variación de los clústers para asignar etiquetas que describan de un modo veraz su naturaleza.
Resulta útil elaborar el perfil de los grupos en términos de las variables utilizadas para el conglomerado, como los datos demográficos, los psicográficos, uso del producto, uso de los medios u otras variables.
Consideremos un ejemplo para poder comprender mejor el funcionamiento del proceso. Supongamos que estamos interesados en estudiar la dieta eficaz contra la ingesta regular de bebidas ligeras.
Para ello, se confeccionó una escala de evaluación de la actitud del encuestado que se componía de siete aseveraciones diferentes. De este modo, los individuos entrevistados arrojaron valores de 1 a 7 puntos. Las afirmaciones que formaban parte de la escala de siete puntos eran del tipo: las bebidas ligeras dietéticas saben más fuerte, las bebidas dietéticas son más sanas, etc.
Se convino en recoger los datos demográficos y los datos de consumo de bebidas refrescantes por su relevancia para el estudio planteado.
Como se dijo anteriormente, en esta fase se examinan los promedios de la puntuación de los perfiles. Para nuestro caso concreto, basándonos en la escala de actitud diseñada para cada grupo y poder asignar de esta manera una etiqueta descriptiva a cada uno de ellos.
Supongamos que dos de los grupos resultantes del análisis clúster tuvieran actitudes favorables hacia las bebidas dietéticas ligeras y un tercer grupo actitudes negativas. Se podría manejar la posibilidad de que, de los dos grupos favorables en actitud, uno de ellos fuera favorable sólo hacia las bebidas dietéticas ligeras y el otro favorable tanto hacia refrescos ligeros como hacia refrescos normales.
Evaluaríamos entonces las actitudes de cada clúster y desarrollaríamos interpretaciones substantivas para facilitar el etiquetado de cada grupo. Por ejemplo, uno de los clúster podría etiquetarse como individuos conscientes de la salud y las calorías y el otro como individuos indiferentes a una subida de azúcar.
Con respecto al perfilado de los conglomerados o grupos, cabe decir que no es más que la descripción de las características de cada clúster para explicar cómo podrían inferir en dimensiones relevantes.
Para conseguir esto, se recurre normalmente al empleo del Análisis Discriminante o a algún otro estadístico apropiado. El analista utiliza los datos no incluidos previamente en el procedimiento de aglomeración para perfilar las características de cada clúster.
Estos datos suelen ser características demográficas, perfiles psicográficos, pautas de consumo, etc.
Aplicando este proceso y extrapolándolo al ejemplo de las bebidas concluiríamos que el clúster individuos conscientes de la salud y las calorías radica en una mejor educación o en mayores ingresos profesionales al ser consumidores moderados de bebidas refrescantes.
En resumen, el análisis de perfiles se enfoca a describir no a lo que determinan directamente los clústers sino (una vez se han determinado los distintos grupos) a sus características propias.
Por ello, se hace especial énfasis en las características que definen los grupos y en la capacidad de los miembros de cada conglomerado para predecir una actitud particular del clúster en cuestión.
8. Validación de Conglomerados Obtenidos
Dados los criterios generales que comprende el AC, no debe aceptarse ninguna solución de agrupación sin una evaluación de su confianza y validez. La validación es el intento por parte del analista de asegurar que los clúster obtenidos sean representativos de la población original y que sean generalizables a otros objetos y estables a lo largo del tiempo.
Los siguientes procedimientos ofrecen revisiones adecuadas de la calidad de los resultados de la agrupación:
- Realizar el AC con los mismos datos y utilizar distintas medidas de distancia. Comparar los resultados con todas las medidas a fin de determinar la estabilidad de las soluciones.
- Utilizar diversos métodos de conglomerado y comparar los resultados.
- Dividir los datos a la mitad de forma aleatoria. Realizar el AC por separado en cada mitad (submuestra). Comparar las soluciones de los dos análisis y evaluar la correspondencia de los resultados o bien comparar los centroides de grupo de las dos submuestras.
- Eliminar las variables de forma aleatoria. Realizar la agrupación basándose en el conjunto reducido de variables. Comparar los resultados basados en el conjunto completo con los que se obtuvieron al realizar el conglomerado.
- En el conglomerado no jerárquico la solución puede depender del orden de los casos en el conjunto de datos. Para estudiar esto, es recomendable llevar a cabo corridas múltiples y utilizar distintos órdenes de los casos hasta estabilizar la solución.
Definición de Variables
Se define como variables la propiedad que puede variar y cuya variación es susceptible de medirse. Ejemplos: sexo, motivación hacia el trabajo, personalidad, exposición a una campaña, calidad del servicio.
En el trabajo con formulaciones hipotéticas resulta de vital importancia la definición del tipo de relaciones que se establecen entre las variables, puesto que la verificación depende del grado en que se puedan demostrar esas relaciones. Esto exige mucha precisión en el uso de los términos lógicos que enlazan a las variables, ya que una expresión mal utilizada puede desvirtuar completamente el sentido de la formulación.
Las relaciones entre variables pueden clasificarse como sigue:
- Reversible: si X, entonces Y, y si Y entonces X, o irreversible: si X, entonces Y, pero sí Y, no hay conclusión respecto a X.
- Determinista: si X, entonces siempre Y, o estocástica: si X, entonces probablemente Y.
- Secuencial: si X, entonces más tarde Y, o coexistente: si X, entonces también Y.
- Suficiente: si X, entonces independientemente de otra cosa, Y, o contingente: si X, entonces Y, pero solo si Z.
- Necesaria: si X, y solo X, entonces Y, o sustituible: si X, entonces Y, pero si Z, también Y.
- Interdependiente: cuando en la relación se combinan los atributos de reversibilidad, contingencia y secuencialidad, por ejemplo: si X, varía a Xi, Xii, Xiii…., entonces Y varía también a Yi, Yii, Yiii…., etcétera.
Una vez que se han establecido con precisión las relaciones entre las variables, es preciso realizar su operacionalización, o sea, identificar las dimensiones, indicadores, escalas y categorías con las que puede constatarse la presencia de la variable que interesa medir.
En la teoría investigativa se han definido tres tipos de variables, que corrientemente aparecen en los diseños hipotéticos: variables dependientes, independientes y ajenas. No creemos necesario profundizar sobre las características de cada una, aún cuando abundan los ejemplos en que se confunde la relación entre las dos primeras o no se toman en consideración las que actúan paralelamente a la relación principal.
En cualquier variable se pueden distinguir dimensiones cuantitativas y cualitativas. Las dimensiones de las variables también pueden ser espaciales y temporales. Otro tipo de dimensiones son las contextuales y situacionales, además las dimensiones de la variable pueden ser individuales y grupales.
Este asunto requiere de un profundo análisis previo del objeto de estudio, para que puedan establecerse con exactitud todas las dimensiones e indicadores que identifican a la variable seleccionada. A partir de aquí podrá elaborarse una hipótesis sólida y verificable.
En el siguiente esquema se presenta el análisis de las dimensiones posibles para dos variables seleccionadas en un ejemplo de un grupo de estudiantes, donde se seleccionan el Rendimiento y la Disciplina escolar:
| Dimensiones | Rendimiento | Disciplina |
| Cuantitativa | Porcentaje de aprobados | Cantidad de hechos |
| Cualitativa | Calidad de las calificaciones | Trascendencia, magnitud |
| Objetiva | Calificaciones | Sanciones y estímulos |
| Subjetiva | Criterios sobre el redimiento (de los maestros, alumnos, padres, funcionarios y otros). | Criterios sobre la disciplina (de los maestros, alumnos, padres, funcionarios y otros). |
| Espaciales | En los exámenes, trabajos de clase, tareas extraclase y otros. | En el aula, taller, área de deportes, biblioteca y otros. |
| Temporales | Semanal, mensual, semestral, curso escolar, carrera, etc. | Semanal, mensual, semestral, curso escolar, carrera, etc. |
| Contextual | En ejercicios programados o sorpresivos. | Bajo control del docente, o de otras personas. |
| Situacional | En los controles parciales, finales o de selectividad. | En las actividades docentes, extradocentes, recreativas, etc. |
| Individual | Rendimiento individual, por asignatura, período y curso. | Cumplimiento individual de las normas disciplinarias. |
| Grupal | Rendimiento grupal, por asignatura, período y curso. | Cumplimiento individual de lasnormas disciplinarias. |
A partir de estos elementos estudiados se procede a la selección o definición de variables, para ello se consultaron diversas bibliografías.
Atendiendo a la relación existente con la investigación que se realiza y los elementos finales que perseguimos se seleccionó un estudio realizado por Guimaraes, Sandy y McKeen (2003) para el Quality Managetmen Journal Vol.10. Issue4. October 2003, titulado «Comprobación empírica de algunos factores relacionados con el desarrollo de sistemas de calidad», en el cual se realiza un profundo estudio con datos de más de 228 sistemas de calidad para seleccionar variables que inciden en la calidad del servicio por ellos seleccionado, teniendo en cuenta los aspectos allí tratados y tomados como base fundamental para la determinar las variables de esta investigación se han definido como variables para realizar el Análisis de Conglomerados las siguientes:
- Cantidad de Auditorías que se realizan: Esta variable indica la cantidad de Auditorías realizadas por cada territorio teniendo en cuenta la dimensión de los mismos y sus características territoriales.
- Cantidad de auditores con que cuenta el sistema: Nos permite saber los Recursos Humanos con que cuenta el sistema en los diferentes territorios, indica además el déficit o satisfacción de las necesidades de Recursos Humanos implicados en la prestación del servicio.
- Calificación de los Auditores: Es la experiencia adquirida del proveedor del servicio, no todos los proveedores tienes la misma capacitación. La experiencia del proveedor es obtenida a través del adiestramiento en la preparación de las tareas que deben realizar y en la ejecución de las mismas.
- Características del sistema empresarial: El sistema empresarial de los territorios puede ser homogéneo o heterogéneo, dependiendo de las características y el desarrollo de cada territorio esto implica que el servicio de Auditoría que se presta sea diferente en cuanto a cantidad de Auditorías a realizar, el número de auditores implicados, los recursos que se comprometen, el tiempo de ejecución de Auditorías, recalificación y formación de los Recursos Humanos.
Bibliografía:
Aiteco Consultores, Métodos y Herramientas.
Barredo Prieto, Manuel. Filosofías de Calidad.
Benitez Miranda, Miguel Angel, Miranda Dearubas, María Victoria. Contabilidad y Finanzas para la formación económica de los cuadros de dirección /Angel Miguel Benitez Miranda, Maria Victoria Mirandas Dearubas. — Ministerio de la Industria Ligera, 1997.
Blázquez Moral, Juan. Auditoría. Juan Blázquez Moral. Editorial Nacional de Cuba, La Habana, 1965
Bolten, Steven E. Administración Financiera. E. Steven Bolten. Editorial Limusa S.A. Balderas. Universidad de Houston. México. DF, 1995.
Cantú. Desarrollo de una cultura de Calidad. Cantú, H.D., Mc Graw_Hill. 2001.
Colectivo de autores. CECOFIS. Diplomado en Auditoría General. Manual de autoestudio. Tomo 1 y 2 del 2001
_______, Principios de la Auditoría. Ciudad de La Habana. Cuba.
_______, Regulaciones sobre Normas de Auditoría. Oficina Nacional de Auditoría. Cuba, 1999.
Colín, Leticia. “Las normas ISO 9000-2000 de Sistemas de Gestión de la Calidad”
Cook, John W. y Winkle, Gary M. Auditoría, 3° Edición, McGRAW-HILL, Buenos Aires-Argentina, 1987.
Cospin, M Oswaldo. 7 Herramientas básicas para el control de calidad.
De Miranda, Antonio; Torras, Oscar. Auditoría de las empresas socialistas/ Antonio de Miranda, Oscar Torras. Universidad de la Habana. La Habana, 1974.
Decreto Ley # 159 de Auditoría. Oficina Nacional de Auditoría. Cuba , 1995.
Echevarría Hernández, Rogelio. La Auditoría Interna. Rogelio Echevarria Hernandez. Ministerio de Finanzas y Precios, 1994.
Evans, James R. y Lindsay, William M. La Administración y el Control de la Calidad. International Thomson Editores. México, 2000
GestioPolis.com. Normas de calidad. Disponible en: www.gestiopolis.com/recursos/documentos/fulldocs/ger/normascalidad.htm
Gómez Avilés, Bismayda. Gestión de la calidad. Conceptos, terminología y enfoques. Cuba, 2002
Guimaraes, Sandy y McKeen(2003) QMJ Vol.10 Issue 4. October 2003.
Heckmann, Gerardo.Medición de la Calidad de los Servicios.
Hernández, Hugo. Generaciones de la calidad.
Holmes, Arthur W.: Auditoría: principios y procedimientos. W Arthur Holmes. Editorial Hispanoamérica. México.1952
Internetworking Technologies Handbook. Capítulo 49. “Quality of Service Networking”.
ISO 9000- 2000. Sistemas de gestión de la calidad. principios y vocabulario.
Juran, Joseph Moses. Manual de Control de la Calidad. Joseph Moses Juran. Graw_Hill. 5. Edición. 2001.
La Página de la Calidad. Las 7 Herramientas de la Calidad.
León Lefcovich, Mauricio. Kaizen – La Mejora Continua aplicada en la Calidad, Productividad y Reducción de Costos.
Mendoza Aquino, José Antonio. Medición de la calidad del servicio.
Microsoft Corporation. “Resumen de los mecanismos de QoS y cómo interoperan”, 2004.
Ministerio de Auditoría y Control. Manual del MAC. 2000
Moreno, Joaquín. Las Finanzas en la empresa. Cuarta Edición. México, 1989.
Paton, W.A. Manual del contador. W. A. Paton. México Utecha, 1943.
Poblete, Fernando. Normas de Auditoria.
Pons Murguía, Ramón. Notas de clase Maestría Ing. Industrial. Conferencias impartidas por Dr. C. Ramón Pons Murguía
Resolución No. 2/97, Oficina Nacional de Auditoría. Cuba, 1997
Revista » Auditoría y Control» Ministerio de Auditoría y Control.No 4 del 2001
Revista “Auditoría y Control” Ministerio de Auditoría y Control.No 8 Abril 2003
Revista “Auditoría y Control” Ministerio de Auditoría y Control. Volumen I, No 3. Edición.
Sanguinetti, Corabel. Análisis y Diseño de Sistema.
Universitas Miguel Hernández. Herramientas de la Calidad.
Vilar Barrio, José Francisco. Las 7 nuevas herramientas para la mejora de la calidad, 2ª edición.
Weston, J. Fred y Capeland, Thomas E. Finanzas y Administración. Novena Edición. México, 1996.
Zabaro Babani, León. Auditoría y Control. Leon Zabaro Babani. Septiembre –Diciembre, 2000.

