Este trabajo de investigación documental se trata de ayudar al investigador a saber como debe ir estructurada la investigación, teniendo en cuenta que lo primero es seleccionar un tema, y que la problemática sea vigente, y así darle solución, ya que todo problema aparece a raíz de una dificultad, la cual se origina a partir de una necesidad.
La investigación documental debe de llevar planteamiento del problema, investigación experimental, variables, hipótesis, su metodología, la estadística, medidas de tendencia central, medidas de dispersión, tabulación y gráficas.
Para llevar acabo una investigación se debe tener bien claro el planteamiento del problema, para posteriormente llevar acabo la hipótesis, la cual se va encargar de darle forma a la investigación, ya que nos llevará a elaborar el objetivo que se desea alcanzar, el diseño de investigación factible a la problemática, la selección del método, los instrumentos, las técnicas y seleccionar los recursos, tanto humanos como materiales con los cuales se llevarán la investigación a realizar.
Por tanto para realizar la investigación se requiere saber, si ya alguien había investigado referente a la problemática, para que de ahí se retome la indagación y se le de solución a la problemática.
Para realizar una investigación, el investigador debe saber el significado de cada concepto de los pasos a seguir en una investigación documental, para lo cual le presentamos la definición de cada uno de ellos.
EL MARCO TEÓRICO DE UNA INVESTIGACIÓN
Carlos Sabino (1996), afirma que «el planteamiento de una investigación no puede realizarse si no se hace explícito aquello que nos proponemos conocer: es siempre necesario distinguir entre lo que se sabe y lo que no se sabe con respecto a un tema para definir claramente el problema que se va a investigar». El correcto planteamiento de un problema de investigación nos permite definir sus objetivos generales y específicos, como así también la relimitación del objeto de estudio.
El autor agrega que ningún hecho o fenómeno de la realidad puede abordarse sin una adecuada conceptualización.
El investigador que se plantea un problema, no lo hace en el vacío, como si no tuviese la menor idea del mismo, sino que siempre parte de algunas ideas o informaciones previas, de algunos referentes teóricos y conceptuales, por más que éstos no tengan todavía un carácter preciso y sistemático.
El marco teórico, marco referencial o marco conceptual tiene el propósito de dar a la investigación un sistema coordinado y coherente de conceptos y proposiciones que permitan abordar el problema. «Se trata de integrar al problema dentro de un ámbito donde éste cobre sentido, incorporando los conocimientos previos relativos al mismo y ordenándolos de modo tal que resulten útil a nuestra tarea».
El fin que tiene el marco teórico es el de situar a nuestro problema dentro de un conjunto de conocimientos, que permita orientar nuestra búsqueda y nos ofrezca una conceptualización adecuada de los términos que utilizaremos.
«El punto de partida para construir un marco de referencia lo constituye nuestro conocimiento previo de los fenómenos que abordamos, así como las enseñanzas que extraigamos del trabajo de revisión bibliográfica que obligatoriamente tendremos que hacer».
El marco teórico responde a la pregunta: ¿qué antecedentes existen? Por ende, tiene como objeto dar a la investigación un sistema coordinado y coherente de conceptos, proposiciones y postulados, que permita obtener una visión completa del sistema teórico y del conocimiento científico que se tiene acerca del tema.
Ezequiel Ander-Egg [1990] nos dice que en el marco teórico o referencial «se expresan las proposiciones teóricas generales, las teorías específicas, los postulados, los supuestos, categorías y conceptos que han de servir de referencia para ordenar la masa de los hechos concernientes al problema o problemas que son motivo de estudio e investigación». En este sentido, «todo marco teórico se elabora a partir de un cuerpo teórico más amplio, o directamente a partir de una teoría. Para esta tarea se supone que se ha realizado la revisión de la literatura existente sobre el tema de investigación. Pero con la sola consulta de las referencias existentes no se elabora un marco teórico: éste podría llegar a ser una mezcla ecléctica de diferentes perspectivas teóricas, en algunos casos, hasta contrapuestas. El marco teórico que utilizamos se deriva de lo que podemos denominar nuestras opciones apriorísticas, es decir, de la teoría desde la cual interpretamos la realidad».
Roberto Hernández Sampieri y otros [2000] destacan las siguientes funciones que cumple el marco teórico dentro de una investigación:
- Ayuda a prevenir errores que se han cometido en otros estudios.
- Orienta sobre cómo habrá de realizarse el estudio (al acudir a los antecedentes, nos podemos dar cuenta de cómo ha sido tratado un problema específico de investigación, qué tipos de estudios se han efectuado, con qué tipo de sujetos, cómo se han recolectado los datos, en qué lugares se han llevado a cabo, qué diseños se han utilizado).
- Amplía el horizonte del estudio y guía al investigador para que se centre en su problema, evitando desviaciones del planteamiento original.
- Conduce al establecimiento de hipótesis o afirmaciones que más tarde habrán de someterse a prueba en la realidad.
- Inspira nuevas líneas y áreas de investigación.
- Provee de un marco de referencia para interpretar los resultados del estudio.
En general, se podría afirmar que el marco teórico tiene también como funciones:
– Orientar hacia la organización de datos y hechos significativos para descubrir las relaciones de un problema con las teorías ya existentes.
– Evitar que el investigador aborde temáticas que, dado el estado del conocimiento, ya han sido investigadas o carecen de importancia científica.
– Guiar en la selección de los factores y variables que serán estudiadas en la investigación, así como sus estrategias de medición, su validez y confiabilidad.
– Prevenir sobre los posibles factores de confusión o variables extrañas que potencialmente podrían generar sesgos no deseados.
– Orientar la búsqueda e interpretación de dato
1.1 LA ELABORACIÓN DEL MARCO TEÓRICO
La elaboración del marco teórico comprende, por lo general, dos etapas:
– Revisión de la literatura existente. Consiste en destacar, obtener y consultar la bibliografía y otros materiales que pueden ser útiles para los propósitos de estudio, de donde se debe extraer y recopilar la información relevante y necesaria que atañe a nuestro problema de investigación.
– Adopción de una teoría o desarrollo de una perspectiva teórica. En este aspecto, nos podemos encontrar con diferentes situaciones:
- Que existe una teoría completamente desarrollada, con abundante evidencia empírica y que se aplica a nuestro problema de investigación. En este caso, la mejor estrategia es tomar esa teoría como la estructura misma del marco teórico.
- Que hay varias teorías que se aplican a nuestro problema de investigación. En este caso, podemos elegir una y basarnos en ella para construir el marco teórico o bien tomar partes de algunas o todas las teorías, siempre y cuando se relacionen con el problema de estudio.
III. Que hay «piezas o trozos» de teoría con apoyo empírico moderado o limitado, que sugieren variables importantes, aplicables a nuestro problema de investigación. En este caso resulta necesario construir una perspectiva teórica.
- Que solamente existen guías aún no estudiadas e ideas vagamente relacionadas con el problema de investigación. En este caso, el investigador tiene que buscar literatura que, aunque no se refiera al problema específico de la investigación, lo ayude a orientarse dentro de él.
Una vez realizadas las lecturas pertinentes, estaremos en posición de elaborar nuestro marco teórico, que se basará en la integración de la información relevada.
El orden que llevará la integración estará determinado por el objetivo del marco teórico. Si, por ejemplo, es de tipo histórico, resulta recomendable establecer un orden cronológico de las teorías y/o de los hallazgos empíricos. Si la investigación se relaciona con una serie de variables y tenemos información de teoría, así como de estudios previos de cada una de esas variables y de la relación entre ellas, sería conveniente delimitar secciones que abarcaran cada uno de los aspectos relevantes, a fin de integrar aquellos datos pertinentes a nuestro estudio.
De todos modos, es fundamental en toda investigación que el autor incorpore sus propias ideas, críticas o conclusiones con respecto tanto al problema como al material recopilado. También es importante que se relacionen las cuestiones más sobresalientes, yendo de lo general a lo concreto, es decir, mencionando primero generalidades del tema, hasta llegar a lo que específicamente está relacionado con nuestra investigación.
1.2 PLANTEAMIENTO DEL PROBLEMA
Generalmente es una de las etapas más breves de una investigación; sin embargo, en ocasiones, puede llegar a ser la etapa más larga del proceso, debido a causas como pueden ser falta de información, poca visión, falta de comunicación, etc.
La pregunta es la pauta que sugiere el sentido de búsqueda; las acciones, medios, recursos, técnicas o procedimientos involucrados serán convenientes en la medida que favorezcan a proporcionar los datos que permitan dar forma a la respuesta.
La pregunta puede expresar varias ideas por lo que se deben tomar en cuenta los siguientes puntos para la realización del problema de investigación:
¿Qué se quiere investigar?
¿Cómo se quiere investigar?
¿Hasta donde se quiere investigar?
¿Con qué elementos se cuenta para la realización de la investigación?
¿Para qué se quiere investigar?
¿Con cuanto tiempo se dispone?
Las expresiones interrogativas, determinan la condición del asunto al realizar la pregunta: qué, quién, dónde, como, cuándo, etc., son los vocablos que señalan una cuestión en particular, por ejemplo:
¿Qué relación existe entre las variables X y Y?
¿Tiene relevancia práctica?,
¿Me interesa?,
¿Es importante?,
¿Se basa en investigaciones previas?
¿Es actual?
Debe el planteamiento, ser correcto y preciso, importante y bien delimitado, para evitar que se acumulen datos que pueden ser irrelevantes y por lo mismo se aprecie una falta de datos necesarios. Para que sea preciso hay que delimitar el ámbito de estudio.
La investigación debe ser un análisis penetrante de un problema limitado, y no un examen superficial de un amplio campo de estudio.
Así entonces en el planteamiento de un problema siempre se consideran los conocimientos adquiridos con anterioridad; pero, comprendiéndolos como una pretensión por resolver las incógnitas que el propio desarrollo del conocimiento contiene y además, en el problema se señalan fundamentalmente, los resultados de la experimentación y del desarrollo teórico que no se pueden explicar por completo con apoyo de los conocimientos anteriores.
1.3 DELIMITACIÓN DEL PROBLEMA
Como cualquier fenómeno del universo el problema de investigación no es estático sino que corresponde a una dinámica. Ya que los problemas existen en un estado de latencia (sus manifestaciones aún no son evidentes) esperando ser reconocidos.
Aunque el problema este latente, no siempre se reconoce en su totalidad, parte de él puede ser identificado cuando algo de éste se manifiesta, por lo tanto al visualizar el problema tal vez se encuentren varios enigmas con aspectos que requieren respuesta, si eso sucede, se deben reducir o ubicar en metas que se puedan abordar a un solo estudio, por consiguiente hay que plantearlo de forma adecuada, con un lenguaje claro y conciso, es decir hay que delimitarlo.
La identificación y clara delimitación de un problema con miras a su investigación científica no es algo fácil de lograr, pues no existen reglas para ello; el acto mismo de «inventar» o descubrir un problema es algo que escapa al análisis lógico.
Sin embargo, pensar verdaderamente un problema determinado que sea teóricamente significativo y, en principio investigable, puede convertirse en una empresa de reflexión muy cuidadosa y que no suele emprenderse sin un mínimo de vocación.
Lo que sucede generalmente que cuando uno se plantea un problema que cree que ya esta delimitado al ir consultando más información resulta que se derivan una serie de preguntas que para nosotros pueden ser problemas, de tal manera que nuestro problema original resulta un problema muy general, por lo que la última pregunta de la cual ya no se derive otra que nos interese será nuestro problema a investigar.
- 4 FORMULACIÓN DE LAS HIPÓTESIS
Podemos definir la hipótesis como un intento de explicación o una respuesta «provisional» a un problema de investigación. Su función consiste en delimitar el problema que se va a investigar según algunos elementos tales como el tiempo, el lugar, las características de los sujetos, etc.
Llegar a comprobar o rechazar la hipótesis que se ha elaborado previamente, confrontando su enunciado teórico con los hechos empíricos, es el objetivo primordial de todo estudio que pretenda explicar algún campo de la realidad.
Para plantear una hipótesis adecuada, debemos tener en cuenta los siguientes puntos:
Los términos que se empleen deben ser claros y concretos para poder definirlos de manera operacional, a fin de que cualquier investigador que quiera replicar la investigación, pueda hacerlo. Una hipótesis sin referencia empírica constituye un juicio de valor. Si una hipótesis no puede ser sometida a verificación empírica, desde el punto de vista científico no tiene validez.
Las hipótesis deben ser objetivas y no llevar algún juicio de valor; es decir, no debe definirse el fenómeno con adjetivos tales como «mejor» o «peor», sino solamente tal y como pensamos que sucede en la realidad.
Las hipótesis deben ser específicas, no sólo en cuanto al problema, sino a los indicadores que se van a emplear para medir las variables que estamos estudiando.
Las hipótesis deben estar relacionadas con los recursos y las técnicas disponibles. Esto quiere decir que cuando el investigador formule su hipótesis debe saber si los recursos que posee son adecuados para la comprobación de la misma.
La hipótesis debe estar directamente relacionada con el marco teórico de la investigación y derivarse de él.
Las hipótesis deben ser producto de la observación objetiva y su comprobación, estar al alcance del investigador.
REQUISITOS DE LAS HIPÓTESIS
Las hipótesis deben:
Establecer las variables a estudiar, es decir, especificar las variables a estudiar, fijarles límite.
Establecer relaciones entre variables, es decir, la hipótesis debe ser especificada de tal manera que sirva de base a inferencias que nos ayuden a decidir si explica o no los fenómenos observados. Las hipótesis deben establecer relaciones cuantitativas entre variables.
Mantener la consistencia entre hechos e hipótesis, ya que éstas se cimentan, al menos en parte, sobre hechos ya conocidos. Por tanto, las hipótesis no deben establecer implicaciones contradictorias o inconsistentes con lo ya verificado en forma objetiva.
TIPOS DE HIPÓTESIS
Hipótesis nula. Para todo tipo de investigación en la que tenemos dos o más grupos, se establecerá una hipótesis nula.
La hipótesis nula es aquella que nos dice que no existen diferencias significativas entre los grupos.
Por ejemplo, supongamos que un investigador cree que si un grupo de jóvenes se somete a un entrenamiento intensivo para las Olimpíadas de Matemática, éstos serán mejores para resolver problemas que aquellos que no recibieron entrenamiento. Para demostrar su hipótesis toma al azar una muestra de jóvenes, y también al azar los distribuye en dos grupos: uno que llamaremos experimental, el cual recibirá entrenamiento, y otro que no recibirá entrenamiento alguno, al que llamaremos control. La hipótesis nula señalará que no hay diferencia en el desempeño de la resolución de problemas entre el grupo de jóvenes que recibió el entrenamiento y el que no lo recibió.
Una hipótesis nula es importante por varias razones:
Es una hipótesis que se acepta o se rechaza según el resultado de la investigación.
El hecho de contar con una hipótesis nula ayuda a determinar si existe una diferencia entre los grupos, si esta diferencia es significativa, y si no se debió al azar.
No toda investigación precisa de formular hipótesis nula. Recordemos que la hipótesis nula es aquella por la cual indicamos que la información a obtener es contraria a la hipótesis de trabajo.
Al formular esta hipótesis, se pretende negar la variable independiente.
Es decir, se enuncia que la causa determinada como origen del problema fluctúa, por tanto, debe rechazarse como tal.
Otro ejemplo:
Hipótesis: el aprendizaje de los niños se relaciona directamente con su edad.
Hipótesis nula: no existe diferencia significativa entre el aprendizaje en niños de diversas edades.
Hipótesis conceptual. Es la hipótesis que se formula como resultado de las explicaciones teóricas aplicables a nuestro problema. Nos ayuda a explicar desde el punto de vista teórico el fenómeno que estamos investigando.
Es la hipótesis orientadora de la investigación, intenta enfocar el problema como base para la búsqueda de datos. No puede abarcar más de lo propuesto en los objetivos de la investigación o estar en desacuerdo con ellos. Podemos enunciarla como una relación causal o determinante proveniente del planteamiento del problema, de donde se desprenden las variables
Hipótesis de trabajo. Es aquella que le sirve al investigador como base de su investigación, o sea, trata de dar una explicación tentativa al fenómeno que se está investigando. Ésta es la hipótesis que el investigador tratará de aceptar como resultado de su investigación, rechazando la hipótesis nula.
Se dice que la hipótesis de trabajo es operacional por presentar cuantitativamente (en términos medibles) la hipótesis conceptual o general.
Hipótesis alternativa. Al responder a un problema, es muy conveniente proponer otras hipótesis en que aparezcan variables independientes distintas de las primeras que formulamos. Por tanto, para no perder tiempo en búsquedas inútiles, es necesario hallar diferentes hipótesis alternativas como respuesta a un mismo problema y elegir entre ellas cuáles y en qué orden vamos a tratar su comprobación.
Las hipótesis, naturalmente, serán diferentes según el tipo de investigación que se esté realizando. En los estudios exploratorios, a veces, el objetivo de la investigación podrá ser simplemente el de obtener los mínimos conocimientos que permitan formular una hipótesis.
También es aceptable que, en este caso, resulten poco precisas, como cuando afirmamos que «existe algún tipo de problema social en tal grupo», o que los planetas poseen algún tipo de atmósfera, sin especificar de qué elementos está compuesta.
Los trabajos de índole descriptiva generalmente presentan hipótesis del tipo «todos los X poseen, en alguna medida, las característica Y». Por ejemplo, podemos decir que todas las naciones poseen algún comercio internacional, y dedicarnos a describir, cuantificando, las relaciones comerciales entre ellas. También podemos hacer afirmaciones del tipo «X pertenece al tipo Y», como cuando decimos que una tecnología es capital – intensiva. En estos casos, describimos, clasificándolo, el objeto de nuestro interés, incluyéndolo en un tipo ideal complejo de orden superior.
Por último, podemos construir hipótesis del tipo «X produce (o afecta) a Y», donde estaremos en presencia de una relación entre variables.
Sólo en los casos de investigaciones explicativas es necesario formular claramente cuáles son las hipótesis de la investigación. En las investigaciones descriptivas y, con más razón, en las exploratorias, es posible omitir las hipótesis, ya sea porque éstas son tan amplias y poco definidas que dicen muy poco a quien lee el informe de investigación, o porque no es posible o necesario verificarlas.
Dificultades para la formulación de hipótesis:
Falta de conocimientos o ausencia de claridad en el marco teórico.
Falta de aptitud para la utilización lógica del marco teórico.
Desconocimiento de las técnicas adecuadas de investigación para redactar
Hipótesis en debida forma.
Utilidad de las hipótesis:
El uso y formulación correcta de las hipótesis le permiten al investigador poner a prueba aspectos de la realidad, disminuyendo la distorsión que pudieran producir sus propios deseos o gustos. Pueden ser sometidas a prueba y demostrarse como probablemente correctas o incorrectas sin que interfieran los valores o creencias del individuo.
Estructura de las hipótesis
Una hipótesis generalmente se especifica por la estructura SI – ENTONCES (cuando intervienen dos variables). Cuando las variables son más de dos, las estructuras más frecuentes son:
- Si P, entonces Q, bajo las condiciones R y S.
- Si P1, P2 y P3, entonces Q.
- 5 DETERMINACIÓN DE LAS VARIABLE
La definición más sencilla, es la referida a la capacidad que tienen los objetos y las cosas de modificar su estado actual, es decir, de variar y asumir valores diferentes. Sabino (1980) establece:
«entendemos por variable cualquier característica o cualidad de la realidad que es susceptible de asumir diferentes valores, es decir, que puede variar, aunque para un objeto determinado que se considere puede tener un valor fijo».
Briones (1987 : 34) define:
«Una variable es una propiedad, característica o atributo que puede darse en ciertos sujetos o pueden darse en grados o modalidades diferentes. . . son conceptos clasificatorios que permiten ubicar a los individuos en categorías o clases y son susceptibles de identificación y medición».
CLASIFICACIÓN DE LAS VARIABLES
Variable Independiente:
Es aquella característica o propiedad que se supone ser la causa del fenómeno estudiado. En investigación experimental se llama así, a la variable que el investigador manipula.
Variable Dependiente:
Hayman (1974 : 69) la define como propiedad o característica que se trata de cambiar mediante la manipulación de la variable independiente.
La variable dependiente es el factor que es observado y medido para determinar el efecto de la variable independiente.
Variable Interviniente:
Son aquellas características o propiedades que de una manera u otra afectan el resultado que se espera y están vinculadas con las variables independientes y dependientes.
Variable Moderadora:
Según Tuckman: representan un tipo especial de variable independiente, que es secundaria, y se selecciona con la finalidad de determinar si afecta la relación entre la variable independiente primaria y las variables dependientes.
Variables Cualitativas:
Son aquellas que se refieren a atributos o cualidades de un fenómeno. Sabino (1989 : 80) señala que sobre este tipo de variable no puede construirse una serie numérica definida.
Variable Cuantitativa:
Son aquellas variables en las que características o propiedades pueden presentarse en diversos grados de intensidad, es decir, admiten una escala numérica de medición.
Variables Continuas:
Son aquellas que pueden adoptar entre dos números puntos de referencias intermedio. Las calificaciones académicas (10.5, 14.6, 18.7, etc.)
Variables Discretas:
Son aquellas que no admiten posiciones intermedias entre dos números. Ej., en Barinas la división de territorial la constituyen 11 municipios por no (10.5 u 11.5 municipios).
Variables de Control:
Según Tuckman: La define como esos factores que son controlados por el investigador para eliminar o neutralizar cualquier efecto que podrían tener de otra manera en el fenómeno observado.
Operacionalización de la Variable:
Es un paso importante en el desarrollo de la investigación. Cuando se identifican las variables, el próximo paso es su operacionalización.
2.1 INVESTIGACIÓN EXPERIMENTAL
Investigación experimental es un tipo de investigación que usa la lógica y los principios encontrados en las ciencias naturales. Los experimentos pueden ser llevados a cabo en el laboratorio o en la vida real.
Estos generalmente involucran un número relativamente pequeño de personas y abordan una pregunta bastante enfocada. Los experimentos son más efectivos para la investigación explicativa y frecuentemente están limitados a temas en los cuales el investigador puede manipular la situación en la cual las personas se hallan.
En la mayoría de estos experimentos, el investigador divide a las personas objeto de la investigación en dos o más grupos.
Los dos grupos reciben tratamientos idénticos, excepto que el investigador da a un grupo y no a los otros la condición en la que el estáinteresado: el tratamiento.
El investigador mide las reacciones de ambos grupos con precisión. Mediante el control de las condiciones de ambos grupos y dándole el tratamiento a uno de ellos, el investigador puede concluir que las diferentes reacciones de los grupos son debidas únicamente al tratamiento.
CARACTERÍSTICAS DE LA METODOLOGÍA EXPERIMENTAL
Definición: Un experimento es un estudio en el que al menos una variable es manipulada y las unidades son aleatoriamente asignadas a los distintos niveles o categorías de las variables manipuladas. (Pedhazur y Pedhazur, 1991)
Características del diseño experimental:
- Manipulación: es la intervención deliberada del investigador para provocar cambios en la v. dependiente.
- Aleatorización: mayor tamaño de los efectos frente a la equiparación.
Todos los diseños experimentales se caracterizan por la manipulación, pero pueden ser clasificados atendiendo a la aleatorización en:
- Auténticamente experimentales.
- Cuasiexperimentales.
En los diseños experimentales la aleatorización es como se distribuyen los sujetos en los diferentes grupos que forman parte del estudio. El primer ensayo clínico aleatorizado se efectuó en 1.947 por Sir Austin Bradford Hill y lo llevó a cabo sobre el efecto de la Estreptomicina en la Tuberculosis, es el primer estudio realizado con un diseño experimental, hasta ese momento el diseño investigador que se realizaba era el “estudio de casos”, estudios observacionales simples.
La aleatorización mide y reduce el error.
En las Ciencias de la Salud como es tan importante estudiar los efectos que produce una variable, sus consecuencias y la relación causa-efecto que se puede producir, es muy importante conocer el error y reducirlo en todo lo posible, por ello los estudios de investigación deben ser y deben reunir la característica de la aleatorización, por ello deben utilizarse diseños experimentales.
Ejemplo: Estudio de incidencia de Ca de pulmón. Para llevarlo a cabo se cogerían dos grupos de personas que deberán reunir idénticas características en cuanto al mismo número de individuos que lo componen, grupos de edad que lo forman e idéntica proporción en cuanto al género, posteriormente se procedería a la comparación e investigación de Ca de pulmón en cada uno de los grupos.
VENTAJAS DEL DISEÑO EXPERIMENTAL
- Se elimina el efecto de las variables perturbadoras o extrañas, mediante el efecto de la aleatorización.
- El control y manipulación de las variables predictorias clarifican la dirección y naturaleza de la causa.
- Flexibilidad, eficiencia, simetría y manipulación estadística.
Viabilidad de los diseños experimentales
- Imposibilidad de manipular algunas variables.
- Cuestiones éticas.
- Practicabilidad.
INCONVENIENTES DEL DISEÑO EXPERIMENTAL
- Dificultad de elegibilidad y manejo de las variables de control.
- Dificultad de disponer de muestras representativas.
- Falta de realismo.
CALIDAD DEL DISEÑO EXPERIMENTAL
- Validez Interna.
- Validez Externa.
- Validez Ecológica.
- Validez de Constructo
2.2 METODOLOGÍA
Etapas que el investigador debe realizar para llevar a cabo una investigación experimental.
*Presencia de un problema. Para el cual se ha realizado una revisión bibliográfica.
*Identificación y definición del problema.
*Definición de hipótesis y variables y la operación de las mismas.
*Diseño del plan experimental.
-Diseño de investigación.
-Determinación de la población y muestra.
-Selección de instrumentos de medición.
-Elaboración de instrumentos.
-Procedimientos para obtención de datos.
*Prueba de confiabilidad de datos.
*Realización del experimento.
*Tratamiento de datos. Aquí en este punto hay que tener en cuenta que una cosa es el dato bruto, otro el dato procesado y otro, el dato que hay que dar como definitivo
2.3. LA ESTADISTICA EN LA INVESTIGACIÓN
El proceso de aplicación de la estadística implica una serie de pasos:
Selección y determinación de la población o muestra y las características contenidas que se desean estudiar. En el caso de que se desee tomar una muestra, es necesario determinar el tamaño de la misma y el tipo de muestreo a realizar (probabilístico o no probabilístico).
Obtención de los datos. Esta puede ser realizada mediante la observación directa de los elementos, la aplicación de encuestas y entrevistas, y la realización de experimentos.
Clasificación, tabulación y organización de los datos. La clasificación incluye el tratamiento de los datos considerados anómalos que pueden en un momento dado, falsear un análisis de los indicadores estadísticos. La tabulación implica el resumen de los datos en tablas y gráficos estadísticos.
Análisis descriptivo de los datos. El análisis se complementa con la obtención de indicadores estadísticos como las medidas: de tendencia central, dispersión, posición y forma.
Análisis inferencial de los datos. Se aplican técnicas de tratamiento de datos que involucran elementos probabilísticos que permiten inferir conclusiones de una muestra hacia la población (opcional).
Elaboración de conclusiones. Se construye el informe final.
2.4 MEDIDAS DE TENDENCIA CENTRAL Y DE DISPERSIÓN
Distribución de frecuencias.
Distribución de Frecuencias. Es un agrupamiento de datos en categorías mutuamente excluyentes dando el número de observaciones en cada categoría.
Los pasos para obtener una distribución de frecuencia son los siguientes:
1) Determinar el número de clases que se quiere. Un método para determinar el número de clases es la regla “2 a la k”. Esta regla sugiere seleccionar como el número de clases el menor número (k), tal que 2 a la k sea mayor que el número de datos (n).
2) Determinar el intervalo o la amplitud de clase. Generalmente el tamaño de la clase o del intervalo debe ser el mismo para todas las clases. Las clases juntas deben abarcar por lo menos la distancia entre el menor valor de los datos en bruto hasta el valor mayor. Expresado en la siguiente fórmula:
i = H – L / k
Donde:
i = intervalo de clase
H = mayor valor observado
L = menor valor observado
k = número de clases
Generalmente el resultado de la fórmula se redondea a algún número adecuado, como por ejemplo un múltiplo de 10 o de 100.
3) Fijar los límites de cada clase. Se trata de fijar los límites de cada clase de modo que cada observación se pueda colocar sólo en una clase. Se deben evitar los límites de clase que sean poco claros o que se sobrepongan.
4) Poner una marca por cada observación que quede en cada clase.
5) Contar en número de observaciones en cada clase (frecuencia de clase)
La frecuencia relativa se obtiene dividiendo la frecuencia de clase entre el total de datos (n). La frecuencia porcentual se obtiene multiplicando la frecuencia relativa por 100.
2.5 TABULACIÓN Y PRESENTACIÓN GRAFICA
Las representaciones gráficas de las distribuciones de frecuencia, se hacen por lo general con llamadas gráficas de barras (en las que las clases se indican en el eje horizontal y las frecuencias de clase en el eje vertical) o con gráficas de pie, especialmente utilizadas para mostrar las frecuencias porcentuales.
Es importante mencionar que si bien, las representaciones gráficas sirven para dar una visión rápida de la forma en que se comportan los datos, también pueden ser utilizadas (dependiendo de cómo se configuren) para dar una idea equivocada de la información que se quiere presentar.
Medidas de tendencia central
El propósito de cualquier medida de tendencia central es indicar con precisión el centro de un conjunto de observaciones. Algunas de las medidas de tendencia central más comunes son la media, la mediana y la moda.
Media aritmética
La media aritmética es probablemente la medida de tendencia central más importante, en tato es la más utilizada. También se le llama promedio y la vemos aplicada a diario en casi todos los espacios y medio dedicados a brindar información. Algunos ejemplos puedan ser el saldo promedio de una cuenta bancaria, el salario promedio de los empleados de una empresa, el promedio de calificaciones de un estudiante, etc.
Definida formalmente, la media aritmética es la suma de todos los valores de una muestra o población dividida entre el número de valores de la población o muestra.
Cuando lo que se calcula es la media de una población, ésta se representa con la letra griega “ “. Por otro lado, cuando lo que se calcula es la media de una muestra, ésta se representa con “ x “. Así, las fórmulas son como sigue:
Media poblacional = X
N
Dónde:
= Media poblacional
X = Representa cualquier valor particular
N = Número de individuos en la población
= Indica la operación de adición
Media muestral x = X
n
Dónde:
x = Media poblacional
X = Representa cualquier valor particular
n = Número de individuos en la población
= Indica la operación de adición
Algunas características de la media aritmética son:
– Todo conjunto de datos de intervalo o de razón tienen una media.
– Un conjunto de datos sólo tiene una media.
– La media es útil para comparar dos poblaciones.
– La media aritmética es la única medida de tendencia central en la que la suma de las desviaciones de los valores de la media será siempre cero.
Expresado simbólicamente (X – x ) = 0
Mediana
Alguna veces, cuando en un conjunto de datos existen uno o dos muy grandes o muy pequeños, la media aritmética puede no ser representativa. En esos casos, el punto central de ese grupo de datos se puede describir mejor utilizando la mediana.
La mediana es la observación central de los valores de una población o muestra una vez que éstos han sido ordenados de forma ascendente o descendente. Para un número par de observaciones, la mediana es el promedio de los dos valores intermedios.
Algunas características de la mediana son:
-Todo conjunto de datos ordinales, de intervalo o de razón tienen una mediana.
-Un conjunto de datos sólo tiene una mediana.
-A la mediana no le afectan valores extremadamente grandes ni extremadamente pequeños, por eso es especialmente útil cuando se tienen estos valores.
Moda
La moda es el valor que aparece con más frecuencia en un conjunto de datos. La moda es especialmente útil para encontrar el punto central de un grupo de datos de tipo nominal u ordinal.
Algunas características de la moda son:
-Se puede determinar la moda en grupos de datos de todos los niveles (nominales, ordinales, de intervalo y de razón).
-Puede existir más de una moda para cada grupo de datos.
-A la moda no le afectan valores extremadamente grandes ni extremadamente pequeños, por eso es especialmente útil cuando se tienen estos valores.
Otras medidas de tendencia central
Otras medidas de tendencia central que se usa con frecuencia son la media ponderada y la media geométrica. A continuación se da una breve explicación de ambas.
La media ponderada es un caso especial de la media aritmética. Se presenta cuando se tienen varios datos con un mismo valor, lo que puede ocurrir cuando éstos se han agrupado en una distribución de frecuencia. La fórmula que se utiliza es:
Media ponderada x = (wX)
w
Dónde:
x = Media poblacional
X = Representa cualquier valor particular
= Indica la operación de adición
w = Indica el peso o número de repeticiones de cada valor
Por su parte la media geométrica es útil para encontrar el promedio de porcentajes, proporciones, índices o tasas de crecimiento. Por su definición, la media geométrica de un conjunto de n números enteros positivos es la n-ésima raíz del producto de los n valores. La fórmula que se utiliza es la siguiente:
Media Geométrica GM = n √ (X1) (X2) . . . (Xn)
Dónde:
GM = Media poblacional
X = Representa cualquier valor particular
n = Número de individuos en la población
Esta misma medida de tendencia aplicada a problemas de incremento porcentual promedio es como sigue:
Incremento porcentual GM = n √ Valor al final del período – 1
Promedio en el tiempo Valor al inicio del período
Medidas de dispersión
Las medidas de dispersión se utilizan para obtener información complementaria a las medidas de tendencia central y miden la forma como se distribuyen los datos que integran una población o muestra. Así, el rango se basa en la localización de los valores mayor y menor de un grupo de datos, y la varianza y la desviación estándar en las desviaciones de cada uno de los datos que integran la población o muestra con respecto de su media.
Varianza
La varianza es una de las medidas de tendencia central más reportadas, y como ya se mencionó, se basa en la diferencia entre el valor de cada observación y la media.
En términos conceptuales la varianza es la media aritmética de las desviaciones de la media elevadas al cuadrado.
Cuando lo que se calcula es la varianza de una población, ésta se representa con la letra griega “σ2” (elevada al cuadrado), y cuando lo que se calcula es la varianza de una muestra se representa con la letra “s2” (también elevada al cuadrado). Las fórmulas para calcular cada una son como sigue:
Es importante resaltar que la fórmula de la varianza muestral para cálculos tiene la ventaja de que no se necesita calcular la media para obtenerla
PRESENTACIONES EN TABLAS
Primero definiré que es una tabla para luego trabajar las diferentes clases de tablas pedidas:
Una tabla es un cuadro que consiste en la disposición conjunta, ordenada y normalmente totalizada, de las sumas o frecuencias totales obtenidos en la tabulación de los datos, referentes a las categorías o dimensiones de una variable o de varias variables relacionadas entre sí.
Las tablas sistematizan los resultados cuantitativos y ofrecen una visión numérica, sintética y global del fenómeno observado y de las relaciones entre sus diversas características o variables. En ella, culmina y se concreta definitivamente la fase clasificatoria de la investigación cuantitativa.
Teniendo la definición de lo que es una tabla, podemos trabajar entonces cada uno de los tipos de tablas pedidos:
Tabla de entrada de datos: Es una tabla en la cual solo aparecen los datos que se obtuvieron de la investigación científica o del experimento. Es la tabla más sencilla y se utiliza cuando no se necesita mayor información acerca de los datos, estas tablas se construyen por medio de la tabulación de los datos, este procedimiento es relativamente sencillo, para realizarlo nos ocupamos de un conjunto de datos estadísticos obtenidos al registrar los resultados de una serie de n repeticiones de algún experimento u observación aleatoria, suponiendo que las repeticiones son mutuamente independientes y se realizan en condiciones uniformes, es importante decir que el resultado de cada observación puede expresarse de forma numérica, para este tipo de tablas de entrada de datos se puede trabajar con una ó mas variables, de manera que nuestro material estadístico consiste en n valores observados de la variable Xj.
Los valores observados se suelen registrar, en primer lugar en una lista, si él numero de observaciones no excede de 20 ó 30, estos datos se registran en orden creciente de magnitud.
Con los datos de esta tabla pueden hacerse diversas representaciones gráficas y calcularse determinadas características numéricas como la media, la mediana, etc.
EJ: Agrupar en una tabla de datos
10, 1, 6, 9, 2, 5, 7, 4, 3, 8
| X | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
MÉTODOS GRÁFICOS
Primero definiré lo que es un gráfico o diagrama en estadística
Un diagrama es una especie de esquemático, formado por líneas, figuras, mapas, utilizado para representar, bien datos estadísticos a escala o según una cierta proporción, o bien los elementos de un sistema, las etapas de un proceso y las divisiones o subdivisiones de una clasificación. Entre las funciones que cumplen los diagramas se pueden señalar las siguientes:
Hacen más visibles los datos, sistemas y procesos
Ponen de manifiesto sus variaciones y su evolución histórica o espacial.
Pueden evidenciar las relaciones entre los diversos elementos de un sistema o de un proceso y representar la correlación entre dos o más variables.
Sistematizan y sintetizan los datos, sistemas y procesos.
Aclaran y complementan las tablas y las exposiciones teóricas o cuantitativas.
El estudio de su disposición y de las relaciones que muestran puede sugerir hipótesis nuevas.
Algunos de los diagramas más importantes son el diagrama en árbol, diagrama de áreas o superficies, diagrama de bandas, diagrama de barras, diagrama de bloques, diagrama circular, diagrama circular polar, diagrama de puntos, diagrama de tallo y hoja diagrama, histogramas y gráficos de caja y bigote o boxplots.
Gráficos univariados
Para trabajar los gráficos univariables debemos primero saber lo que es el análisis estadístico univariable y después de esto trabajaremos los métodos pedidos
El análisis estadístico que opera con datos referentes a una sola variable o distribución de frecuencias y pretende determinar sus propiedades estadísticas. El a.e.u. proporciona al analista medidas representativas de la distribución o promedios, índices de dispersión de los datos de la distribución, procedimientos para normalizar los datos, medidas de desigualdad de unos datos en relación con otros y por ultimo medidas de la asimetría de la distribución.
Gráficos de puntos: Es una variación del diagrama lineal simple el cual esta formado por líneas rectas o curvas, que resultan de la representación, en un eje de coordenadas, de distribuciones de frecuencias, este construye colocando en el eje x los valores correspondientes a la variable y en el eje de las ordenadas el valor correspondiente a la frecuencia para este valor. Proporciona principalmente información con respecto a las frecuencias. Este se usa cuando solo se necesita información sobre la frecuencia.
Cuando la muestra se agrupa por intervalos se trabaja con la marca de clase del intervalo de clase, la marca de clase es el punto medio del intervalo
EJ: Duración de tubos de neón
| X(horas) | Xm | F |
| 300-400 | 350 | 2 |
| 400-500 | 450 | 6 |
| 500-600 | 550 | 10 |
| 600-700 | 650 | 8 |
| 700-800 | 750 | 4 |
| S 30 |
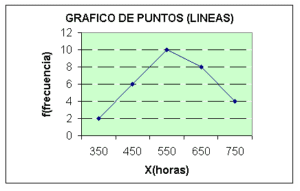
Duración de los tubos de neón
CONCLUSIÓN
Todo trabajo de investigación, se requiere de pasos a seguir para a llevar acabo una investigación de calidad y de tiempo necesario, que no carezca de información, que se tenga las fuentes necesaria y la población a la cual va a ser investigada y más que nada que no pierda su objetivo.
Por lo tanto es de suma importancia que el investigador este empapado de los pasos a seguir en la problemática, que sepa como estructurar un planteamiento de problema, como hacer una hipótesis, cuales sean las variables, el método y su objetivo a seguir para que no haya confusión a la hora de llevar acabo su investigación.
Toda investigación lleva introducción, desarrollo, conclusión, bibliografía y anexos, esta última se le anexa las tablas, graficas y los instrumentos de evaluación o toda aquella información que respalde la investigación, es importante recalcar que el investigador elimine las preferencias personales y los sentimientos ya que podría ocultar los resultados de la investigación.
En la investigación metodológica se lograr a contribuir a una alternativa, la cual responda a la problemática de una sociedad específica, dándole una solución.
REFERENCIAS BIBLIOGRAFÍA:
- Arana Federico. (1975), «Método experimental para principiantes» Edit. Joaquín Motriz, México 77pp
- Bunge Mario (1989),. «La ciencia, su método y su filosofía» Edit. Nueva Imagen Argentina,35-61
- Hernández, R.; C. Fernández y P. Baptisa, (1995), «Metodología de la Investigación», Mc.Graw-Hill, México. 505 pp.
- García –Córdoba F, L:ucía Teresa García – Córdoba., (2004), «La problematización. Una oportunidad para estimular y valorar la generación de investigadores». Edit. Instituto Superior de Ciencias de la Educación del Estado de México. México 58 pp.
- Moreno Rodríguez Diana, Ma del Refugio López Gamiño, Ma. Luisa Cepeda Islas, Patricia Plancarte Cansino e Irma Rosa Al varado Guerrero, (2000), «Planteamiento de Problema», UNAM FES Iztacala pag 5-14
- Pick, Susan y López, Ana Luisa. (1994) CÓMO INVESTIGAR EN CIENCIAS SOCIALES. 5ª ed. México. Ed. Trillas S.A.
- Polit, D. y B. Hungler. 1985. «Investigación científica en ciencias de la salud». 2ª. Interamericana. México. 595pp
- Tamayo y Tamayo, Mario. (1998). El proceso de la investigación científica. 3ª ed. México: Ed. Limusa S.A.


