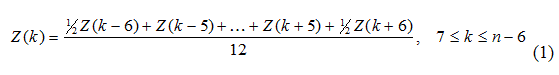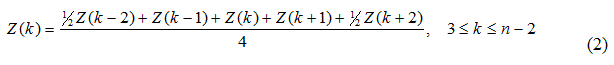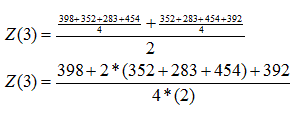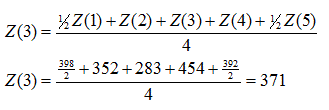¿Se encontró en la situación de tener que hacer ciertos análisis más de una vez? Si es así, ¿le agradaría darle un descanso a su mouse? Con MINITAB usted puede fácilmente automatizar operaciones para ganar tiempo. Hay varias maneras de hacer esto, desde el método fácil y rápido de cortar/pegar, al método más potente usando una macro local.
¿Cómo trabaja esto? Casi todas las operaciones en MINITAB se pueden hacer usando una sesión de comandos. De hecho, cuando usted completa un cuadro de diálogo y hace click en Aceptar, MINITAB genera una sesión de comandos que contiene toda la información que usted seleccionó en él. Usted puede usar esas sesiones de comandos «como están.» o modificarlas si lo desea, cargarlas en un paso y MINITAB ejecutará el análisis entero.
Suponga que tiene una recolección de datos semanal y que genera tres gráficos diferentes desde esos datos. Por supuesto, cada semana debería completar los cuadros de diálogo para los tres gráficos, lo que significaría muchos clicks del mouse. En cambio, usted podría cargar la sesión de comandos que generaron esos gráficos en un único y rápido paso.
Este artículo incluye algunos ejemplos simples de cómo automatizar operaciones de Serie de Tiempos en MINITAB.
Series de Tiempo en Minitab.
Este manual contiene el concepto, aplicación y ejecución en el sistema Minitab versión 15, del tema de Series de Tiempo
CONCEPTOS BASICOS DE SERIES DE TIEMPO
1.1 INTRODUCCIÓN
Toda institución, ya sea la familia, la empresa o el gobierno, tiene que hacer planes para el futuro si ha de sobrevivir y progresar. Hoy en día diversas instituciones requieren conocer el comportamiento futuro de ciertos fenómenos con el fin de planificar, prever o prevenir.
La planificación racional exige prever los sucesos del futuro que probablemente vayan a ocurrir. La previsión, a su vez, se suele basar en lo que ha ocurrido en el pasado. Se tiene pues un nuevo tipo de inferencia estadística que se hace acerca del futuro de alguna variable o compuesto de variables basándose en sucesos pasados. La técnica más importante para hacer inferencias sobre el futuro con base en lo ocurrido en el pasado, es el análisis de series de tiempo.
Son innumerables las aplicaciones que se pueden citar, en distintas áreas del conocimiento, tales como, en economía, física, geofísica, química, electricidad, en demografía, en marketing, en telecomunicaciones, en transporte, etc.
|
Series De Tiempo |
Ejemplos |
| 1. Series económicas: | – Precios de un artículo- Tasas de desempleo- Tasa de inflación
– Índice de precios, etc. |
| 2. Series Físicas: | – Meteorología- Cantidad de agua caída- Temperatura máxima diaria
– Velocidad del viento (energía eólica) – Energía solar, etc. Responde esta encuesta sobre consumo de redes sociales. Nos ayudará a brindarte mejor información. |
| 3. Geofísica: | – Series sismologías |
| 4. Series demográficas: | – Tasas de crecimiento de la población- Tasa de natalidad, mortalidad- Resultados de censos poblacionales |
| 5. Series de marketing: | – Series de demanda, gastos, ofertas |
| 6. Series de telecomunicación: | – Análisis de señales |
| 7. Series de transporte: | – Series de tráfico |
Uno de los problemas que intenta resolver las series de tiempo es el de predicción. Esto es dado una serie {x(t1),…,x(tn)} nuestros objetivos de interés son describir el comportamiento de la serie, investigar el mecanismo generador de la serie temporal, buscar posibles patrones temporales que permitan sobrepasar la incertidumbre del futuro.
En adelante se estudiará como construir un modelo para explicar la estructura y prever la evolución de una variable que observamos a lo largo del tiempo. La variables de interés puede ser macroeconómica (índice de precios al consumo, demanda de electricidad, series de exportaciones o importaciones, etc.), macroeconómica (ventas de una empresa, existencias en un almacén, gastos en publicidad de un sector), física (velocidad del viento en una central eólica, temperatura en un proceso, caudal de un río, concentración en la atmósfera de un agente contaminante), o social (número de nacimientos, matrimonios, defunciones, o votos a un partido político).
1.2 DEFINICIÓN DE SERIE DE TIEMPO
En muchas áreas del conocimiento las observaciones de interés son obtenidas en instantes sucesivos del tiempo, por ejemplo, a cada hora, durante 24 horas, mensuales, trimestrales, semestrales o bien registradas por algún equipo en forma continua.
Llamamos Serie de Tiempo a un conjunto de mediciones de cierto fenómeno o experimento registradas secuencialmente en el tiempo. Estas observaciones serán denotadas por {x(t1), x(t2), …, x(tn)} = {x(t) : t Î T Í R} con x(ti) el valor de la variable x en el instante ti. Si T = Z se dice que la serie de tiempo es discreta y si T = R se dice que la serie de tiempo es continua. Cuando ti+1 – ti = k para todo i = 1,…,n-1, se dice que la serie es equiespaciada, en caso contrario será no equiespaciada.
En adelante se trabajará con series de tiempo discreta, equiespaciadas en cuyo caso asumiremos y sin perdida de generalidad que: {x(t1), x(t2), …, x(tn)}= {x(1), x(2), …, x(n)}.
1.3 PRIMER PASO AL ANALIZAR CUALQUIER SERIE DE TIEMPO
El primer paso en el análisis de series de tiempo, consiste en graficar la serie. Esto nos permite detectar las componentes esenciales de la serie.
El gráfico de la serie permitirá:
a) Detectar Outlier: se refiere a puntos de la serie que se escapan de lo normal. Un outliers es una observación de la serie que corresponde a un comportamiento anormal del fenómeno (sin incidencias futuras) o a un error de medición.
Se debe determinar desde fuera si un punto dado es outlier o no. Si se concluye que lo es, se debe omitir o reemplazar por otro valor antes de analizar la serie.
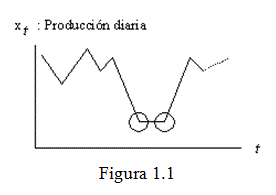
Por ejemplo, en un estudio de la producción diaria en una fábrica se presentó la siguiente situación ver figura 1.1:
Los dos puntos enmarcados en un círculo parecen corresponder a un comportamiento anormal de la serie. Al investigar estos dos puntos se vio que correspondían a dos días de paro, lo que naturalmente afectó la producción en esos días. El problema fue solucionado eliminando las observaciones e interpolando.
b) Permite detectar tendencia: la tendencia representa el comportamiento predominante de la serie. Esta puede ser definida vagamente como el cambio de la media a lo largo de un periodo (ver figura 1.2).
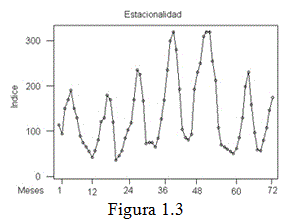
c) Variación estacional: la variación estacional representa un movimiento periódico de la serie de tiempo. La duración de la unidad del periodo es generalmente menor que un año. Puede ser un trimestre, un mes o un día, etc (ver figura 1.3).
Matemáticamente, podemos decir que la serie representa variación estacional si existe un número s tal que x(t) = x(t + k×s).
Las principales fuerzas que causan una variación estacional son las condiciones del tiempo, como por ejemplo:
- en invierno las ventas de helado
- en verano la venta de lana
- exportación de fruta en marzo.
Todos estos fenómenos presentan un comportamiento estacional (anual, semanal, etc.)
d) Variaciones irregulares (componente aleatoria): los movimientos irregulares (al azar) representan todos los tipos de movimientos de una serie de tiempo que no sea tendencia, variaciones estacionales y fluctuaciones cíclicas.
2. MODELOS CLASICOS DE SERIES DE TIEMPO
2.1 MODELOS DE DESCOMPOSICIÓN
Un modelo clásico para una serie de tiempo, supone que una serie x(1), …, x(n) puede ser expresada como suma o producto de tres componentes: tendencia, estacionalidad y un término de error aleatorio.
Existen tres modelos de series de tiempos, que generalmente se aceptan como buenas aproximaciones a las verdaderas relaciones, entre los componentes de los datos observados. Estos son:
- Aditivo: X(t) = T(t) + E(t) + A(t)
- Multiplicativo: X(t) = T(t) • E(t) • A(t)
- Mixto: X(t) = T(t) • E(t) + A(t)
Donde:
- X(t) serie observada en instante t
- T(t) componente de tendencia
- E(t) componente estacional
- A(t) componente aleatoria (accidental)
Una suposición usual es que A(t) sea una componente aleatoria o ruido blanco con media cero y varianza constante.
Un modelo aditivo (1), es adecuado, por ejemplo, cuando E(t) no depende de otras componentes, como T(t), sí por el contrario la estacionalidad varía con la tendencia, el modelo más adecuado es un modelo multiplicativo (2). Es claro que el modelo 2 puede ser transformado en aditivo, tomando logaritmos. El problema que se presenta, es modelar adecuadamente las componentes de la serie.
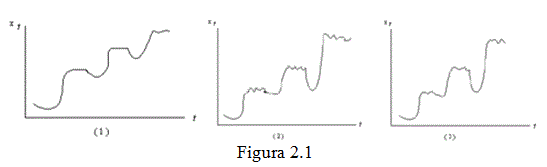
La figura 2.1 ilustra posibles patrones que podrían seguir series representadas por los modelos (1), (2) y (3).
2.2 ESTIMACIÓN DE LA TENDENCIA
Supondremos aquí que la componente estacional E(t) no está presente y que el modelo aditivo es adecuado, esto es:
X(t) = T(t) + A(t), donde A(t) es ruido blanco.
Hay varios métodos para estimar T(t). Los más utilizados consisten en:
- Ajustar una función del tiempo, como un polinomio, una exponencial u otra función suave de t.
- Suavizar (o filtrar) los valores de la serie.
- Utilizar diferencias.
2.2.1 AJUSTE DE UNA FUNCIÓN
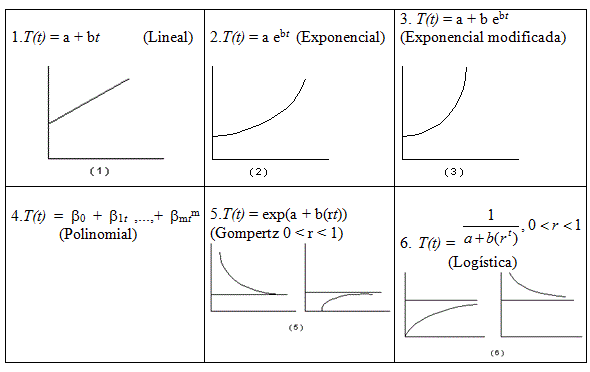
Los siguientes gráficos ilustran algunas de las formas de estas curvas.
Nota:
- la curva de tendencia debe cubrir un periodo relativamente largo para ser una buena representación de la tendencia a largo plazo.
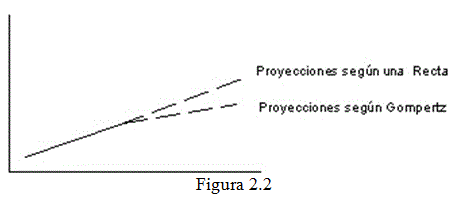
- La tendencia rectilínea y exponencial son aplicable a corto plazo, puesto que una curva S a largo plazo puede parecer una recta en un período restringido de tiempo (por ejemplo).
En la figura 2.2 ambas curvas (recta y Gompertz) ajustan bien pero las proyecciones divergen enormemente a largo plazo.
Ejemplo 1: En la tabla 2.1 se presentan los datos trimestrales de unidades habitacionales iniciadas en los Estados Unidos desde el tercer trimestre de 1964 hasta el segundo trimestre de 1972 [1]. (Es necesario advertir que para el análisis de tendencia el periodo que se considera debería ser más largo. Sin embargo, ya que el propósito principal es el de ilustrar el método de descomposición y las técnicas para inferir partiendo de los elementos así descompuestos, la insuficiencia de los datos no tiene por qué interesar.)
Tabla 2.1: Nuevas unidades habitacionales comenzadas en los Estados Unidos del tercer trimestre de 1964 al segundo trimestre de 1972 (en miles de unidades).
Sea t cada uno de los 32 trimestres que van de 1964 a 1972, o sea que t = 1 para el tercer trimestre de 1964, t = 2 para el cuarto trimestre, y así sucesivamente. Así que el dominio de definición de t es el conjunto de los enteros de 1 a 32 inclusive. Sea T(t) las iniciaciones de viviendas trimestralmente. Los valores de t y T(t) se dan en la tabla 2.2. Para calcular los valores de a y de b en la recta de tendencia
T(t) = a + bt
Se obtienen las siguientes cifras a partir de los datos de la tabla 2.1.
Tabla 2.2: Cálculo de la tendencia de las viviendas comenzadas en los Estados Unidos del tercer trimestre de 1964 al segundo trimestre de 1972
| Año trimestre |
t |
T(t) |
Tendencia |
| 1964: 3 |
1 |
398 |
291,73 |
|
4 |
2 |
352 |
298,07 |
| 1965: 1 |
3 |
283 |
304,41 |
|
2 |
4 |
454 |
310,75 |
|
3 |
5 |
392 |
317,09 |
|
4 |
6 |
345 |
323,43 |
| 1966: 1 |
7 |
274 |
329,77 |
|
2 |
8 |
392 |
336,11 |
|
3 |
9 |
290 |
342,45 |
|
4 |
10 |
210 |
348,79 |
| 1967: 1 |
11 |
218 |
355,13 |
|
2 |
12 |
382 |
361,47 |
|
3 |
13 |
382 |
367,81 |
|
4 |
14 |
340 |
374,15 |
| 1968: 1 |
15 |
298 |
380,49 |
|
2 |
16 |
452 |
386,83 |
|
3 |
17 |
423 |
393,17 |
|
4 |
18 |
372 |
399,51 |
| 1969: 1 |
19 |
336 |
405,85 |
|
2 |
20 |
468 |
412,19 |
|
3 |
21 |
387 |
418,53 |
|
4 |
22 |
309 |
424,87 |
| 1970: 1 |
23 |
264 |
431,21 |
|
2 |
24 |
399 |
437,55 |
|
3 |
25 |
408 |
443,89 |
|
4 |
26 |
396 |
450,23 |
| 1971: 1 |
27 |
389 |
456,57 |
|
2 |
28 |
604 |
462,91 |
|
3 |
29 |
579 |
469,25 |
|
4 |
30 |
513 |
475,59 |
| 1972: 1 |
31 |
510 |
481,93 |
|
2 |
32 |
661 |
488,27 |
Entonces, la recta de tendencia es
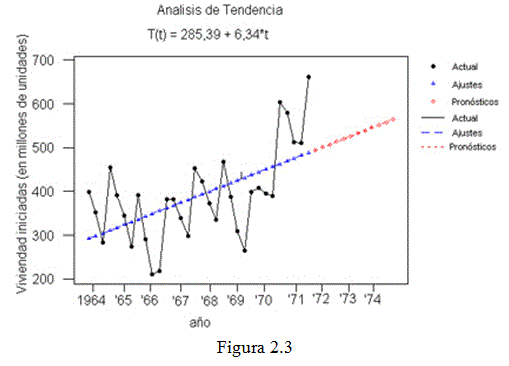
T(t) = 285,39 + 6,34× t
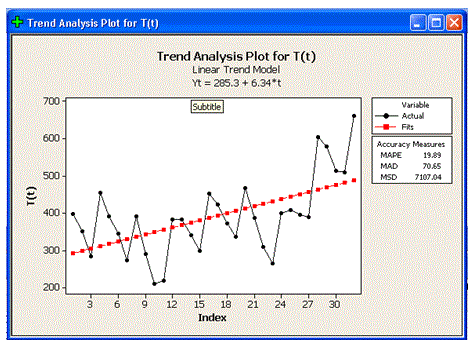
La figura 2.3 muestra gráficamente la recta de tendencia ajustada a los datos trimestrales de la tabla 2.2. La recta de trazos después de 1972 representa proyecciones (ver sección 3 Predicciones).
Desarrollo en Minitab:
- Abrir Minitab.
- Copiar los datos a la hoja de trabajo de Minitab.
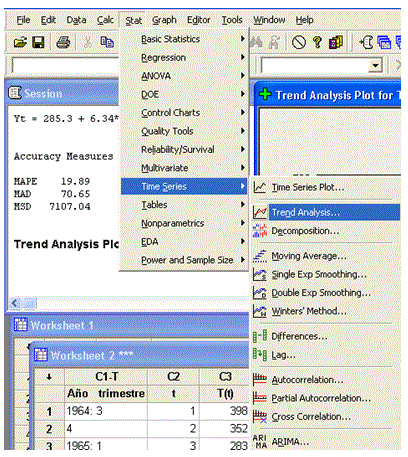
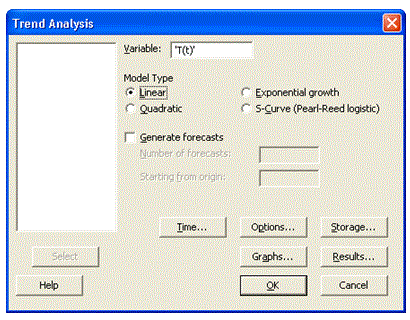
- Seleccionar: Stat à Time Series à Trend Analysis.
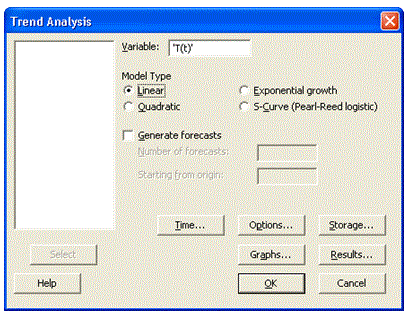
- En la ventana Trend Analysis seleccionamos con un clic la variable, dejamos el Model Type como Linear y clic OK
- Minitab despliega la siguiente gráfica, que como podemos observar es similar a la presentada en el desarrollo del ejercicio.
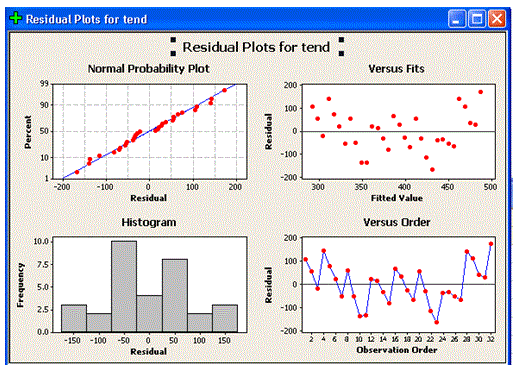
- Si deseamos obtener 4 graficas en una sola ventana seleccionar la opción Graphs…
Clic en Four in one.
Clic OK
Minitab despliega la siguiente gráfica.
2.2.2 SUAVIZAMIENTO. FILTROS LINEALES
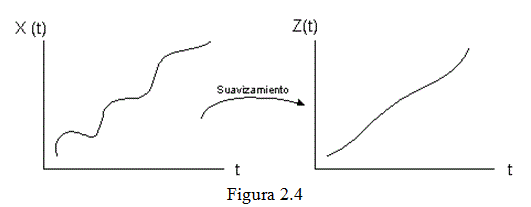
Una forma de visualizar la tendencia, es mediante suavizamiento de la serie. La idea central es definir a partir de la serie observada un nueva serie que suaviza los efectos ajenos a la tendencia (estacionalidad, efectos aleatorios), de manera que podamos determinar la dirección de la tendencia (ver figura 2.4).
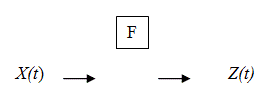
Lo que hacemos es usar una expresión lineal que transforma la serie X(t) en una serie suavizada Z(t): Z(t) = F(X(t)), t = 1,…,n
de tal modo que F(X(t)) = T(t). La función F se denomina Filtro Lineal. El filtro lineal más usado es el promedio móvil.
2.2.2.1 PROMEDIOS MÓVILES
El objetivo es eliminar de la serie las componentes estacionales y accidentales. Para una serie mensual con estacionalidad anual (s = 12), la serie suavizada se obtiene,
Para una serie trimestral, con estacionalidad anual (s = 4), la serie suavizada está dada por
A este procedimiento se les llama: filtro simétrico finito.
Nota: se suaviza cuando existen muchos cambios bruscos, movimientos irregulares.
Ejemplo 2: A partir de los datos del ejemplo1, se calcula un promedio móvil sumando los valores para un cierto número de periodos sucesivos y dividiendo luego la suma así obtenida por el número de períodos abarcados. En este caso se trata de una serie trimestral y para ello se ocupa la fórmula (2).
Tabla 2.3: Cálculo del Promedio Móvil centrado de cuatro trimestres de las iniciaciones de viviendas en los EEUU, tercer trimestre 1964 a segundo trimestre de 1972 (en miles de unidades)
|
Año por trimestre |
Datos Originales Y |
Total Móvil en cuatro trimestres |
Promedio Móvil de cuatro trimestres |
Promedio Móvil Centrado de cuatro trimestres |
|
(1) |
(2) |
(3) |
(4) |
(5) |
| 1964: 3 |
398 |
|||
|
4 |
352 |
|||
| 1965: 1 |
283 |
1.487 |
372 |
371 |
|
2 |
454 |
1.481 |
370 |
369 |
|
3 |
392 |
1.474 |
369 |
367 |
|
4 |
345 |
1.465 |
366 |
359 |
| 1966: 1 |
274 |
1.403 |
351 |
338 |
|
2 |
392 |
1.301 |
325 |
308 |
|
3 |
290 |
1.166 |
292 |
285 |
|
4 |
210 |
1.110 |
278 |
276 |
| 1967: 1 |
218 |
1.100 |
275 |
287 |
|
2 |
382 |
1.192 |
298 |
314 |
|
3 |
382 |
1.322 |
331 |
341 |
|
4 |
340 |
1.402 |
351 |
359 |
| 1968: 1 |
298 |
1.472 |
368 |
373 |
|
2 |
452 |
1.513 |
378 |
382 |
|
3 |
423 |
1.545 |
386 |
391 |
|
4 |
372 |
1.583 |
396 |
398 |
| 1969: 1 |
336 |
1.599 |
400 |
395 |
|
2 |
468 |
1.563 |
391 |
383 |
|
3 |
387 |
1.500 |
375 |
366 |
|
4 |
309 |
1.428 |
357 |
348 |
| 1970: 1 |
264 |
1.359 |
340 |
342 |
|
2 |
399 |
1.380 |
345 |
356 |
|
3 |
408 |
1.467 |
367 |
382 |
|
4 |
396 |
1.592 |
398 |
424 |
| 1971: 1 |
389 |
1.797 |
449 |
471 |
|
2 |
604 |
1.968 |
492 |
507 |
|
3 |
579 |
2.085 |
521 |
536 |
|
4 |
513 |
2.206 |
552 |
559 |
| 1972: 1 |
510 |
2.263 |
566 |
|
|
2 |
661 |
En la tabla 2.3, por ejemplo, el promedio móvil de cuatro trimestres para el primer trimestre de 1965 se obtiene sumando los valores del tercer y cuarto trimestres de 1964 y el primero y segundo trimestres de 1965 y dividiendo luego la suma por 4. El promedio para el segundo trimestre de 1965 se obtiene sumando los valores del cuarto trimestre de 1964 con los del primero, segundo y tercer trimestres de 1965 y luego dividiendo la suma por 4. Así pues, para cada promedio sucesivo, se resta el trimestre que viene primero y se suma el último siguiente.
La columna 4 de la tabla 2.3 muestra los promedios móviles de cuatro trimestres obtenidos, partiendo de los datos iniciaciones de viviendas para el 1964 a 1972. El promedio móvil no elimina las fluctuaciones muy acentuadas de la serie, pero reduce sustancialmente la amplitud de las variaciones de los datos originales.
Si en el cálculo de un promedio móvil entra un número impar de períodos, el proceso será más sencillo puesto que el número de períodos antes y después del período para el cual se calcula el promedio son iguales. Si el número de periodos es par, como en este ejemplo, no se puede utilizar el mismo número de períodos antes y después de un periodo especificado. Por tanto, el promedio móvil ha de quedar a mitad de camino entre los valores de dos períodos consecutivos y no se relaciona con ningún período. Este problema se puede resolver calculando un promedio móvil centrado en la serie, lo cual se logra obteniendo primero un promedio móvil centrado de dos trimestres de los promedios móviles ya obtenidos. El primer promedio móvil centrado es la media de los dos primeros promedios móviles de cuatro trimestres, el segundo promedio móvil centrado es la media de los promedios móviles de cuatro trimestres segundo y tercero, etc. De esta manera, habrá un número igual de períodos después y antes del periodo especificado para el cual se está calculando el promedio móvil centrado. Los promedios móviles centrados se ven en la columna 5 de la tabla 2.3.
Según la fórmula 2, el cálculo sería el siguiente:
Este valor corresponde al Promedio Móvil Centrado que se muestra en la columna 5.
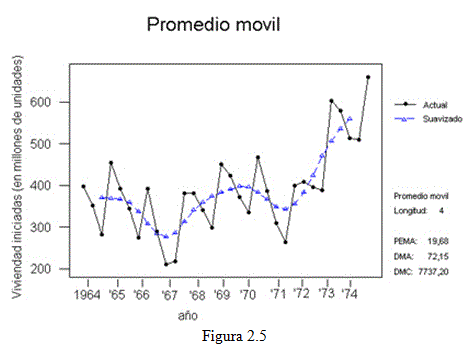
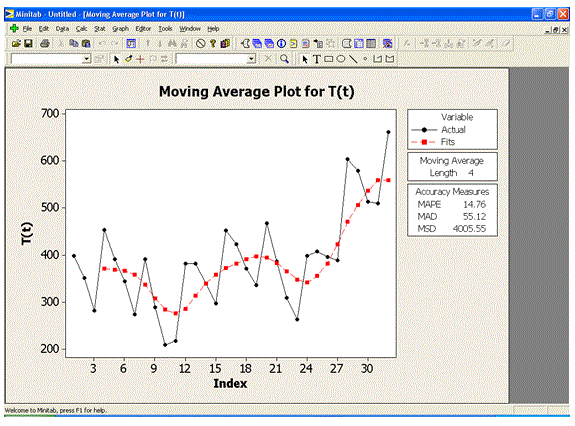
La figura 2.5 muestra gráficamente el ajuste por a través del promedio móvil, según tabla 2.3, donde el segmento negro representa la serie original y el segmento azul la serie suavizada.
Desarrollo en Minitab:
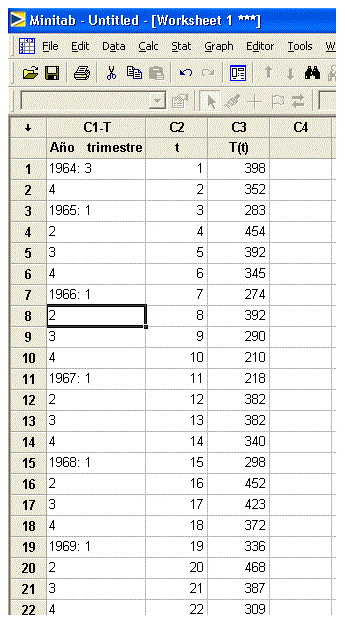
- Abrir Minitab.
- Copiar los datos a la hoja de trabajo de Minitab:
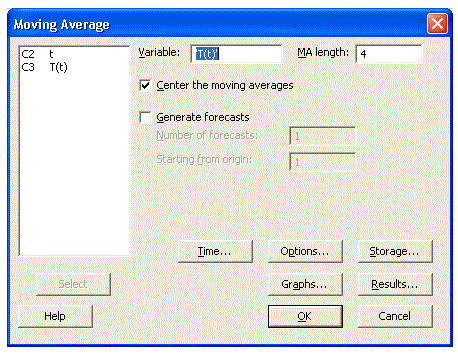
- Seleccionar: Stat à Time Series à Moving Average…
- Seleccionar con un clic la variable con las series de tiempo y colocar la MA length.
En este caso es igual a 4 (4 trimestres por año). Clic OK
- Minitab despliega la gráfica con el promedio móvil.
Resumen
Se llama Serie de Tiempo, a un conjunto de mediciones de cierto fenómeno o experimento registradas secuencialmente en el tiempo, por ejemplo a cada hora, mensualmente, trimestralmente, semestralmente, etc.. En este apunte se trabajó con series de tiempo discreto, equiespaciadas en cuyo caso se asume que: : {x(t1), x(t2), …, x(tn)}= {x(1), x(2), …, x(n)}. Debido al carácter introductorio se restringió al caso de series de tiempo univariadas.
Al analizar una serie de tiempo, lo primero que se debe hacer es graficar la serie. Esto nos permite detectar las componentes esenciales de la serie. El gráfico de la serie permitirá: detectar Outlier, detectar tendencias, variación estacional, variaciones irregulares (o componente aleatoria).
Un modelo clásico para una serie de tiempo, puede ser expresada como suma o producto de tres componentes: tendencia, estacional y un término de error aleatorio. Existen tres modelos de series de tiempos. Estos son:
- Aditivo: X(t) = T(t) + E(t) + A(t)
- Multiplicativo: X(t) = T(t) • E(t) • A(t)
- Mixto: X(t) = T(t) • E(t) + A(t)
Con el fin de obtener un modelo, es necesario estimar la tendencia y la estacionalidad. Para estimar la tendencia, se supone que la componente estacional no está presente. La estimación se logra al ajustar a una función de tiempo a un polinomio o suavizamiento de la serie a través de los promedios móviles. Para estimar la estacionalidad se requiere haber decidido el modelo a utilizar (mixto o aditivo). Una vez estimada la tendencia y la estacionalidad se esta en condiciones de predecir.
Los métodos revisados en este apunte son de naturaleza descriptiva, por lo que el juicio y el conocimiento del fenómeno juegan un rol importante en la selección del modelo.
Los métodos clásicos tienen la desventaja que se adaptan a través del tiempo, lo que implica que el proceso de estimación debe volver a iniciarse frente al conocimiento de un nuevo dato.
Equipo integrado por:
Ing. Gerardo Valdes Fuentes
Ing. Rosa Isela Meléndez López
Lic. José Luis Chávez Dávila
Ing. Renato Elmer Vázquez García
Maestría en Administración y Liderazgo.
Universidad Autónoma del Noreste.
Bibliografía:
Estadística para Administradores,
Richard I. Levin & David S. Rubin.
Editorial Prentice Hall