A continuación encontrarán un un trabajo del área de estadística para ayuda a los procesos de producción.
I.- Objetivo
Aplicar las técnicas estadísticas para el manejo de datos que nos permitan obtener gráficos, medidas de tendencia y calcular probabilidades.
II.- Antecedentes
- Estadística: es la rama de la matemática que nos permite recoger, organizar y analizar datos. Existen dos conceptos importantes dentro de la estadística que nos permiten analizar y estudiar dichos datos, estos son: población y muestra.
- Población: es el conjunto de datos que caracteriza el fenómeno que se desea estudiar.
- Muestra: es un subconjunto de la población a estudiar, el cual es necesario que sea representativo de toda la población.
- Gráfica: es una representación de la relación entre variables, muchos tipos de gráficos aparecen en estadística, según la naturaleza de los datos involucrados y el propósito de la gráfica, es la de representar los valores tabulados obtenidos de los muestreos o los datos del total de la población.
- Distribución de frecuencia: Al resumir grandes colecciones de datos, es útil distribuirlos en clases o categorías, y determinar el número de individuos que pertenecen a cada clase llamado frecuencia de clase. Una disposición tabular de los datos por clases junto con las frecuencias correspondientes de clase se llama distribuidores de frecuencia o tablas de frecuencia.
- Medidas de dispersión: Describen la cantidad de dispersión o variabilidad que se encuentra entre los datos. Datos bastante agrupados poseen valores relativamente pequeños, y datos más dispersos tienen valores más grandes. El agrupamiento más extenso ocurre cuando los datos carecen de dispersión.
III.- Material Utilizado
- Lápiz
- Cuaderno de apuntes
IV.- Herramienta, Equipo
- Calculadora
- Computadora
V.- Desarrollo
Efectuar los siguientes ejercicios:
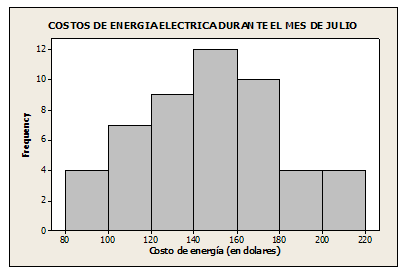
1. Los datos que se muestran a continuación representan el costo de la energía eléctrica durante el mes de julio del 2006 para una muestra aleatoria de 50 departamentos con dos recamaras en una ciudad grande.
Costo de energía eléctrica en dólares.
| 96 | 171 | 202 | 178 | 147 | 102 | 153 | 197 | 127 | 82 |
| 157 | 185 | 90 | 116 | 172 | 111 | 148 | 213 | 130 | 165 |
| 141 | 149 | 206 | 175 | 123 | 128 | 144 | 168 | 109 | 167 |
| 95 | 163 | 206 | 175 | 130 | 143 | 187 | 166 | 139 | 149 |
| 108 | 119 | 150 | 154 | 114 | 135 | 191 | 137 | 129 | 158 |
a) Determine una tabla de frecuencias, para K = 7
| K |
Limites de clase Ls li |
F | Xi | Fi | Hi | Hi |
| 1 | 81 100 | 4 | 90.5 | 4 | 0.08 | 0.08 |
| 2 | 101 120 | 8 | 110.5 | 12 | 0.32 | 0.32 |
| 3 | 121 140 | 12 | 130.5 | 24 | 0.8 | 0.8 |
| 4 | 141 160 | 8 | 150.5 | 32 | 1.44 | 1.44 |
| 5 | 161 180 | 10 | 170.5 | 42 | 2.28 | 2.28 |
| 6 | 181 200 | 4 | 190.5 | 46 | 3.2 | 3.2 |
| 7 | 201 220 | 4 | 210.5 | 50 | 4.2 | 4.2 |
| ?f = 50 |
b) Elabore un histograma de frecuencias y polígono de frecuencias con los datos.
c) Alrededor de qué cantidad parece concentrarse el costo mensual de energía eléctrica.
R = alrededor de 148 (valor de la media)
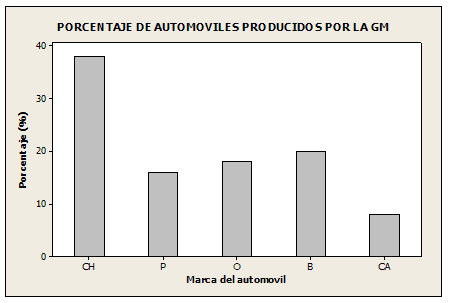
2. Se identificó una muestra de estudiantes que poseía automóviles producidos por la General Motors y se registró la marca de cada automóvil. A continuación se presenta la muestra que se obtuvo (Ch = Chevrolet, P = Pontiac, O = Oldsmobile, B = Buick, Ca = Cadillac):
| Ch | B | Ch | P | Ch | O | B | Ch | Ca | Ch |
| B | Ca | P | O | P | P | Ch | P | O | O |
| Ch | B | Ch | B | Ch | P | O | Ca | P | Ch |
| O | Ch | Ch | B | P | Ch | Ca | O | Ch | B |
| B | O | Ch | Ch | O | Ch | Ch | B | Ch | B |
a) Encuentre el número de automóviles de cada marca que hay en la muestra.
n = 50
| Marca del automovil | Frecuencia |
| Ch | 19 |
| P | 8 |
| O | 9 |
| B | 10 |
| Ca | 4 |
| Total = 50 |
b) ¿Qué porcentaje de estos automóviles son Chevrolet, Pontiac, Oldsmobile,
Buick, Cadillac?
| Marca del automovil | Frecuencia | Porcentaje (%) |
| Ch | 19 | 38 |
| P | 8 | 16 |
| O | 9 | 18 |
| B | 10 | 20 |
| Ca | 4 | 8 |
| Total = 50 | Total = 100 |
c) Trace una gráfica de barras que muestre los porcentajes encontrados en el inciso b).
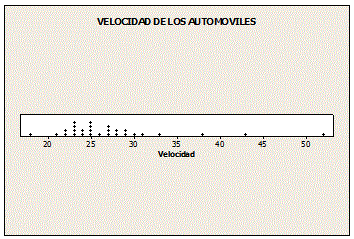
3. Un policía de una ciudad, usando radar, verificó la velocidad de los automóviles que circulaban por una calle de la ciudad:
| 27 | 23 | 22 | 38 | 43 | 24 |
| 25 | 23 | 22 | 52 | 31 | 30 |
| 29 | 28 | 27 | 25 | 29 | 28 |
| 26 | 33 | 25 | 27 | 25 | |
| 21 | 23 | 24 | 18 | 23 |
Elabore una gráfica de puntos para estos datos.
4. Los siguientes son los números de torsiones que se requirieron para cortar 12 barras de aleación forjada: 33, 24, 39, 48, 26, 35, 38, 54, 23, 34, 29 y 27. Determine:
a) La media
x̄ = Σx/n = 410/12
x̄ = 34.17
b) La mediana
x̃ = 33.50
c) El rango promedio
Rango promedio = (Vmenor + Vmayor)/2
Rango promedio = 38.50
5. Por un error, un profesor borró la calificación obtenida por uno de diez alumnos. Si los otros nueve estudiantes obtuvieron 43, 66, 74, 90, 40, 52, 70, 78 y 92 y la media de las diez calificaciones es 67, ¿Qué calificación borró el profesor?
Σx (de 9 datos) = 605
x̄ de 10 datos = 67
x̄ = Σx/n; Σx (de 10 datos) = (x̄)(n) = 67 x 10 = 670
Calificación = x = 670 – 605 = 65
Calificación = 65
6. En los siguientes ejercicios, calcule el rango, el rango promedio, la varianza y la desviación estándar para los datos que se dan.
a) Los valores que se dan son pesos (en onzas) de carnes listadas en el menú de un restaurante como cortes “Porterhouse de 20 onzas” (basados en datos recolectados por un estudiante del autor).
| 17 | 20 | 21 | 18 | 20 | 20 | 20 | 18 | 19 | 19 |
| 20 | 19 | 21 | 20 | 18 | 20 | 20 | 19 | 18 | 19 |
n = 20
Σx = 386
Rango = Valor mayor – Valor menor = 21 – 17
Rango = 4
Rango promedio = (Valor menor + Valor mayor)/2 = (17 + 21)/2
Rango promedio = 19
s2 = 1.168
s = 1.081
b) Dígitos seleccionados en la lotería Maryland Pick Three:
| 0 | 7 | 3 | 6 | 2 | 7 | 6 | 6 | 6 | 3 | 8 | 1 | 7 | 8 | 7 |
| 1 | 6 | 8 | 6 | 9 | 5 | 2 | 1 | 5 | 0 | 3 | 9 | 9 | 0 | 7 |
n = 30
Σx = 148
Rango = Valor mayor – Valor menor = 9 – 0
Rango = 9
Rango promedio = (Valor menor + Valor mayor)/2 = (0 + 9)/2
Rango promedio = 4.5
s2 = 8.754
s = 2.959
c) Concentraciones de alcohol en la sangre de 15 conductores implicados en accidentes mortales y luego condenados a prisión (basados en datos del departamento de Justicia de Estados Unidos).
0.27 0.17 0.17 0.16 0.13 0.24 0.29 0.24
0.14 0.16 0.12 0.16 0.21 0.17 0.18
n = 15
Σx = 2.81
Rango = Valor mayor – Valor menor = 0.29 – 0.12
Rango = 0.17
Rango promedio = (Valor menor + Valor mayor)/2 = (0.12 + 0.29)/2
Rango promedio = 0.205
s2 = 0.00262
s = 0.0512
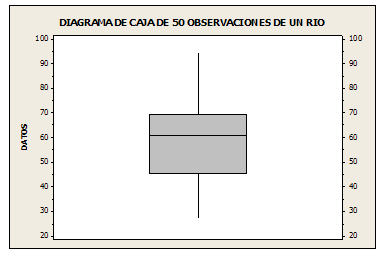
7. La concentración de sólidos suspendidos en agua de un río es una característica ambiental importante. Un artículo científico reportó sobre la concentración (en partes por millón, o ppm) para varios ríos diferentes. Supongamos que se obtuvieron las siguientes 50 observaciones para un río en particular:
| 55.8 | 60.9 | 37.0 | 91.3 | 65.8 |
| 42.3 | 33.8 | 60.6 | 76.0 | 69.0 |
| 45.9 | 39.1 | 35.5 | 56.0 | 44.6 |
| 71.7 | 61.2 | 61.5 | 47.2 | 74.5 |
| 83.2 | 40.0 | 31.7 | 36.7 | 62.3 |
| 47.3 | 94.6 | 56.3 | 30.0 | 68.2 |
| 75.3 | 71.4 | 65.2 | 52.6 | 58.2 |
| 48.0 | 61.8 | 78.8 | 39.8 | 65.0 |
| 60.7 | 77.1 | 59.1 | 49.5 | 69.3 |
| 69.8 | 64.9 | 27.1 | 87.1 | 66.3 |
a) Calcule la media
n = 50
Σx = 2927
x̄ = Σx/n = 2927/50
x̄ = 58.54
b) Calcule la media recortada al 25% y la media recortada al 10%
Media recortada al 25%
50 x 0.25 = 12.5 = 13
n = 50 – (13 valores mínimos + 13 valores máximos) = 50 – 26 = 24
Σx (de 24 datos) = 1423
x̄ = Σx/n = 1423/24
x̄ = 59.31
Media recortada al 10%
50 x 0.10 = 5
n = 50 – (5 + 5) = 50 – 10 = 40
Σx (de 40 datos) = 2333.90
x̄ = Σx/n = 2333.90/40
x̄ = 58.35
c) Calcule la varianza y la desviación estándar
s2 = 270.85
s = 16.46
8. Use los datos del ejercicio 7 (50 observaciones de un río) y calcule lo siguiente:
a) Q1, Q2 y Q3
Para Q1
np = 50 x ¼ = 12.5 = 13
Q1= (45.9 + 47.2)/2 = 46.55
Q1= 46.55
Para Q2
np = 50 x 1/2 = 25
Q2 = (60.7 + 60.9)/2 = 60.8
Q2 = 60.8
Para Q3
np = 50 x 3/4 = 37.5 = 38
Q3 = (69.3 + 69.8)/2 = 69.55
Q3 = 69.55
b) Realice un diagrama de caja con estos datos
c) Calcule P15, P20, P25
P15 = (k/100)n = (15/100) x 50 = 7.5 = 8
P15 = 39.1
P20 = (k/100)n = (20/100) x 50 = 10
P20 = 40
P25 = (k/100)n = (25/100) x 50 = 12.5 = 13
P25 = 45.9
9. Use los datos del ejercicio 1 (costos de energía eléctrica para una muestra de 50 departamentos) y calcule lo siguiente:
a) Q1, Q2 y Q3
Para Q1
np = 50 x ¼ = 12.5 = 13
Q1= (127 + 128)/2 = 127.5
Q1= 127.5
Para Q2
np = 50 x 1/2 = 25
Q2 = (148 + 149)/2 = 148.5
Q2 = 148.5
Para Q3
np = 50 x 3/4 = 37.5 = 38
Q3 = (171 + 172)/2 = 171.5
Q3 = 171.5
b) Calcule el percentil correspondiente a: 191, 70 y 175
Percentil de 191 = 44/50 = 0.88
Percentil de 191 = 0.88
Percentil de 70 = No existe
Percentil de 175 = 39/50 = 0.78
Percentil de 175 = 0.78
c) Realice un diagrama de caja
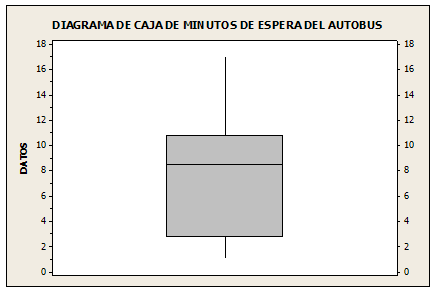
10. Los siguientes son los números de los minutos durante los cuales una persona debió esperar el autobús hacia su trabajo en 15 días laborales: 10, 1, 13, 9, 5, 2, 10, 3, 8, 6, 17, 2, 10 y 15. Determine:
a) La media
x̄ = Σx/n = 111/14
x̄ = 7.93
b) La mediana
x̃ = 8.50
c) Trace un diagrama de caja.
Para Q1
np = 14 x ¼ = 3.5 = 4
Q1= (3 + 5)/2 = 4
Q1= 4
Para Q2
np = 14 x 1/2 = 7
Q2 = (8 + 9)/2 = 8.5
Q2 = 8.5
Para Q3
np = 14 x 3/4 = 10.5 = 11
Q3 = (10 + 13)/2 = 11.5
Q3 = 11.5
VI.- Anexos (Diagramas, dibujos, formulas, ayuda visual, etc.)
VII.- Registro de datos, parámetros, cuestionarios y observaciones
VIII.- Conclusiones y reporte de resultados
IX.- Bibliografía utilizada
Estadística elemental.
Mario f. Triola.
Pearson educación.
Probabilidad y estadística para ingenieros de Miller y Freund
Richard A Johnson.
Prentice Hall.