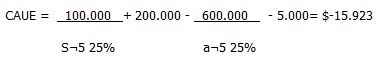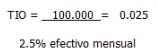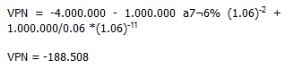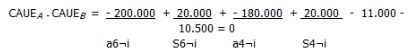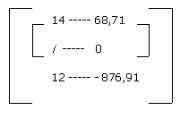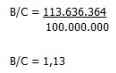Aceptar o rechazar un proyecto en el cual una empresa piense en invertir, depende de la utilidad que este brinde en el futuro frente a los ingresos y a las tasas de interés con las que se evalúe.
Teniendo claros los principios de las matemáticas financieras en la evaluación de proyectos se puede llevar a cabo una valoración más profunda, además es posible comparar con otras alternativas empleando las herramientas que permitan medir las ventajas o desventajas de cada proyecto.
Alternativa Simple: Esta debe aplicarse cuando se evalúa y se tiene que decidir si un proyecto individual es o no conveniente.
Las principales herramientas y metodologías que se utilizan para evaluar un proyecto desde el punto de vista financiero son:
- CAUE: Costo Anual Uniforme Equivalente.
- VPN: Valor Presente Neto.
- VPNI: Valor Presente Neto Incremental.
- TIR: Tasa Interna de Retorno.
- TIRI: Tasa Interna de Retorno Incremental.
- B/C: Relación Beneficio Costo.
- PR: Período de Recuperación.
- CC: Costo Capitalizado.
Todos y cada uno de estos instrumentos de análisis matemático financiero debe conducir a tomar idénticas decisiones económicas, la única diferencia que se presenta es la metodología por la cual se llega al valor final, por ello es sumamente importante tener las bases matemáticas muy claras para su aplicación.
En ocasiones utilizando una metodología se toma una decisión; pero si se utiliza otra y la decisión es contradictoria, es porque no se ha hecho una correcta utilización de los índices.
En la aplicación de todas las metodologías se deben tener en cuenta los siguientes factores que dan aplicación a su estructura funcional:
- C: Costo inicial o Inversión inicial.
- K: Vida útil en años.
- S: Valor de salvamento.
- CAO: Costo anual de operación.
- CAM: Costo anual de mantenimiento.
- IA: Ingresos anuales.
A continuación se analizarán todas las metodologías desde sus bases teóricas, hasta su aplicación a modelos reales.
Costo anual uniforme equivalente (CAUE)
El método del CAUE consiste en convertir todos los ingresos y egresos, en una serie uniforme de pagos. Obviamente, si el CAUE es positivo, es porque los ingresos son mayores que los egresos y por lo tanto, el proyecto puede realizarse ; pero, si el CAUE es negativo, es porque los ingresos son menores que los egresos y en consecuencia el proyecto debe ser rechazado.
A continuación se presenta la aplicación de la metodología del Costo Anual Uniforme Equivalente en la evaluación de proyectos de inversión.
Casi siempre hay más posibilidades de aceptar un proyecto cuando la evaluación se efectúa a una tasa de interés baja, que a una mayor
Ejemplo
Una máquina cuesta $600.000, tiene una vida útil de 5 años y un valor de salvamento de $100.000; el costo anual de operación es de alrededor de $5000 y se estima que producirá unos ingresos anuales del orden de $200.000. Determinar si la compra de la máquina es aconsejable, cuanto se utiliza una tasa de:
- 25%
- 15%
Solución
Utilizando las convenciones indicadas al inicio de este artículo, aplica en el ejemplo así:
C= $600.000
S= $100.000
k= 5 años
CAO= 5.000
Ingresos Anuales (IA) para los Años 1 a 5 $200.000
a) Utilizando i = 25%, se tiene:
Los $600.000 se reparten en una serie uniforme de pagos, que se efectuarán al final de cada uno de los 5 años que dura el proyecto y cada pago tendrá un valor de:
Por otra parte, los $100.000 del valor del salvamento se repartirán en 5 pagos que se efectuarían al final de cada año y tendrían un valor de:
Se puede apreciar que al evaluar el proyecto usando una tasa del 25% no es aconsejable para la empresa realizar esta inversión.
b) Usando i= 15% , se tiene:
En esta evaluación se puede apreciar que en estas condiciones, el proyecto sí es aconsejable.
Como consecuencia de lo anterior, es importante determinar una tasa correcta para hacer los cálculos; hay quienes opinan que debe usarse la tasa promedio, utilizada en el mercado financiero y hay otros que opinan que debe ser la tasa de interés, a la cual normalmente el dueño del proyecto hace sus inversiones. Esta última tasa es conocida con el nombre de Tasa de Interés de Oportunidad (TIO).
Tasa de interés de oportunidad (TIO)
Para ser más claro en este aspecto, analizaremos por medio de algunos ejemplos la TIO.
- Suponga que una persona acostumbra a realizar inversiones en CDT, en los cuales le pagan en promedio el 45% efectivo anual de intereses, entonces se dice que la Tasa de Interés de Oportunidad para esta persona equivaldría a ese mismo 45% efectivo anual.
- Otro caso se daría cuando un comerciante compra mercancías y al venderlas obtiene una ganancia neta del 6% en un mes, en consecuencia para este comerciante la TIO es de 6% efectivo mensual.
Ahora veremos cómo es aplicable esta tasa en la evaluación de proyectos de inversión organizacionales.
Ejemplo
Un señor realiza mensualmente cursos de capacitación en manejo de computadores, con una duración de un mes. El cupo para cada curso es de 15 alumnos y el valor de la matrícula es de $10.000 por alumno; el costo del profesor, mantenimiento de equipos y otros costos ascienden a $50.000 por mes, lo cual da la utilidad neta de:
15 X 10.000 – 50.000 = $100.000
Si su inversión en equipos y mobiliario ascienden a $4.000.000, entonces, su tasa de oportunidad será:
En consecuencia, la TIO es una tasa que varía de una persona a otra y más aún, para la misma persona, varía de tiempo en tiempo.
Cuando un proyecto puede realizarse de diferentes formas, decimos que tiene alternativas que compiten. El siguiente ejemplo analiza el caso en que ingresos y egresos son conocidos.
La evaluación de proyectos por medio de métodos matemáticos- Financieros es una herramienta de gran utilidad para la toma de decisiones por parte de los administradores financieros, ya que un análisis que se anticipe al futuro puede evitar posibles desviaciones y problemas en el largo plazo
A continuación el profesor Julio Moreno explica, a través de un ejemplo muy completo, cómo se calcula el CAUE.
Método del valor presente neto (VPN)
El método del Valor Presente Neto es muy utilizado por dos razones, la primera porque es de muy fácil aplicación y la segunda porque todos los ingresos y egresos futuros se transforman a pesos de hoy y así puede verse, fácilmente, si los ingresos son mayores que los egresos. Cuando el VPN es menor que cero implica que hay una pérdida a una cierta tasa de interés o por el contrario si el VPN es mayor que cero se presenta una ganancia. Cuando el VPN es igual a cero se dice que el proyecto es indiferente.
La condición indispensable para comparar alternativas es que siempre se tome en la comparación igual número de años, pero si el tiempo de cada uno es diferente, se debe tomar como base el mínimo común múltiplo de los años de cada alternativa
Relevante. En la aceptación o rechazo de un proyecto depende directamente de la tasa de interés que se utilice
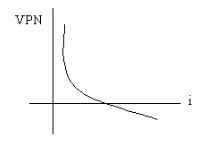
Por lo general el VPN disminuye a medida que aumenta la tasa de interés, de acuerdo con la siguiente gráfica:
En consecuencia para el mismo proyecto puede presentarse que a una cierta tasa de interés, el VPN puede variar significativamente, hasta el punto de llegar a rechazarlo o aceptarlo según sea el caso.
Al evaluar proyectos con la metodología del VPN se recomienda que se calcule con una tasa de interés superior a la Tasa de Interés de Oportunidad (TIO), con el fin de tener un margen de seguridad para cubrir ciertos riesgos, tales como liquidez, efectos inflacionarios o desviaciones que no se tengan previstas.
Ejemplo 1
A un señor, se le presenta la oportunidad de invertir $800.000 en la compra de un lote, el cual espera vender, al final de un año en $1.200.000. Si la TIO es del 30%. ¿Es aconsejable el negocio?
Solución
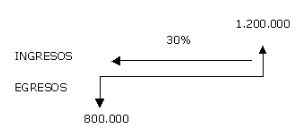
Una forma de analizar este proyecto es situar en una línea de tiempo los ingresos y egresos y trasladarlos posteriormente al valor presente, utilizando una tasa de interés del 30%.
Si se utiliza el signo negativo para los egresos y el signo positivo para los ingresos se tiene:
VPN = – 800.000 + 1.200.000 (1.3)-1
VPN = 123.07
Como el Valor Presente Neto calculado es mayor que cero, lo más recomendable sería aceptar el proyecto, pero se debe tener en cuenta que este es solo el análisis matemático y que también existen otros factores que pueden influir en la decisión como el riesgo inherente al proyecto, el entorno social, político o a la misma naturaleza que circunda el proyecto, es por ello que la decisión debe tomarse con mucho tacto.
Ejemplo 2
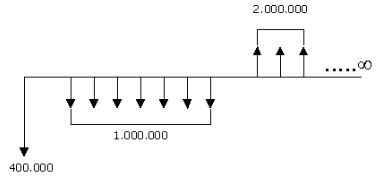
Se presenta la oportunidad de montar 7una fábrica que requerirá una inversión inicial de $4.000.000 y luego inversiones adicionales de $1.000.000 mensuales desde el final del tercer mes, hasta el final del noveno mes. Se esperan obtener utilidades mensuales a partir del doceavo mes en forma indefinida, de
A) $2.000.000
B) $1.000.000
Si se supone una tasa de interés de 6% efectivo mensual, ¿Se debe realizar el proyecto?
Las inversiones que realiza la empresa deben ser constantemente vigiladas y supervisadas por los responsables del área financiera sin excepción
Solución
En primera instancia se dibuja la línea de tiempo para visualizar los egresos y los egresos.
A) Se calcula el VPN para ingresos de $2.000.000.
En este caso el proyecto debe aceptarse ya que el VNP es mayor que cero.
B) Se calcula el VNP para ingresos de $1.000.000
En esta situación el proyecto debe ser rechazado.
En el siguiente par de videos el profesor Xavier Puig, de la Universidad Pompeu Fabra, explica qué es el Valor Presente Neto (VPN), cómo se calcula, cómo se usa y cómo se interpreta.
Método del valor presente neto incremental (VPNI)
El Valor Presente Neto Incremental es muy utilizado cuando hay dos o más alternativas de proyectos mutuamente excluyentes y en las cuales solo se conocen los gastos. En estos casos se justifican los incrementos en la inversión si estos son menores que el Valor Presente de la diferencia de los gastos posteriores.
Para calcular el VPNI se deben realizar los siguientes pasos:
- Se deben colocar las alternativas en orden ascendente de inversión.
- Se sacan las diferencias entre la primera alternativa y la siguiente.
- Si el VPNI es menor que cero, entonces la primera alternativa es la mejor, de lo contrario, la segunda será la escogida.
- La mejor de las dos se compara con la siguiente hasta terminar con todas las alternativas.
- Se deben tomar como base de análisis el mismo periodo de tiempo.
Para analizar este tipo de metodología se presenta el siguiente ejercicio práctico
Ejemplo 1
Dadas las alternativas de inversión A, B y C, seleccionar la más conveniente suponiendo una tasa del 20%.
| Alternativas de inversión | A | B | C |
| Costo inicial | -100.000 | -120.000 | -125.000 |
| Costa anual de operación Año 1 | -10.000 | -12.000 | -2.000 |
| Costa anual de operación Año 2 | -12.000 | -2.000 | -1.000 |
| Costa anual de operación Año 3 | -14.000 | -2.000 | 0 |
Solución
Aquí se debe aplicar rigurosamente el supuesto de que todos los ingresos se representan con signo positivo y los egresos como negativos.
1. A) Primero se compara la alternativa A con la B
| Alternativas de inversión | A | B | B-A |
| Costo inicial | -100.000 | -120.000 | -20.000 |
| Costa anual de operación Año 1 | -10.000 | -12.000 | -2.000 |
| Costa anual de operación Año 2 | -12.000 | -2.000 | +10.000 |
| Costa anual de operación Año 3 | -14.000 | -2.000 | +12.000 |
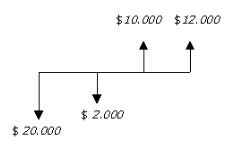
B) La línea de tiempo de los dos proyectos seria:
C) El VPNI se obtiene:
VPNI = -20.000 – 2.000 (1+0.2)-1 + 10.000 (1+0.2)-2 + 12.000 (1+0.2)-3
VPNI = -7.777,7
Como el VPNI es menor que cero, entonces la mejor alternativa es la A.
2. A) Al comprobar que la alternativa A es mejor, se compara ahora con la alternativa C.
| Alternativas de inversión | A | C | C-A |
| Costo inicial | -100.000 | -125.000 | -25.000 |
| Costa anual de operación Año 1 | -10.000 | -2.000 | +8.000 |
| Costa anual de operación Año 2 | -12.000 | -1.000 | +11.000 |
| Costa anual de operación Año 3 | -14.000 | 0 | +14.000 |
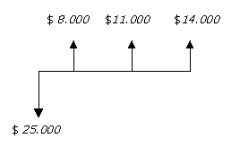
B) La línea de tiempo para los dos proyectos A y C seria:
B) El VPNI se calcula como en el caso anterior
VPN = -25.000 + 8.000 (1+0.2)-1 + 11.000 (1+0.2)-2 + 14.000 (1+0.2)-3
VPN = -2.593
Como el Valor Presente Neto Incremental es menor que cero, se puede concluir que la mejor alternativa de inversión es la A, entonces debe seleccionarse esta entre las tres.
La Tasa Interna de Retorno es la rentabilidad de los dineros que permanecen invertidos en un proyecto
Método de la tasa interna de retorno (TIR)
Este método consiste en encontrar una tasa de interés en la cual se cumplen las condiciones buscadas en el momento de iniciar o aceptar un proyecto de inversión. Tiene como ventaja frente a otras metodologías como la del Valor Presente Neto (VPN) o el Valor Presente Neto Incremental (VPNI) porque en este se elimina el cálculo de la Tasa de Interés de Oportunidad (TIO), esto le da una característica favorable en su utilización por parte de los administradores financieros.
La Tasa Interna de Retorno es aquélla tasa que está ganando un interés sobre el saldo no recuperado de la inversión en cualquier momento de la duración del proyecto. En la medida de las condiciones y alcance del proyecto estos deben evaluarse de acuerdo a sus características, con unos sencillos ejemplos se expondrán sus fundamentos.
Tasa Interna de retorno. Esta es una herramienta de gran utilidad para la toma de decisiones financiera dentro de las organizaciones
Evaluación de proyectos individuales
Ejemplo
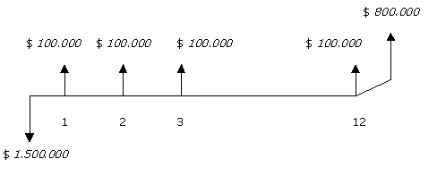
Un terreno con una serie de recursos arbóreos produce por su explotación $100.000 mensuales, al final de cada mes durante un año; al final de este tiempo, el terreno podrá ser vendido en $800.000. Si el precio de compra es de $1.500.000, hallar la Tasa Interna de Retorno (TIR).
Solución
1. Primero se dibuja la línea de tiempo.
2. Luego se plantea una ecuación de valor en el punto cero.
-1.500.000 + 100.000 a12¬i + 800.000 (1 + i)-1 = 0
La forma más sencilla de resolver este tipo de ecuación es escoger dos valores para i no muy lejanos, de forma tal que, al hacerlos cálculos con uno de ellos, el valor de la función sea positivo y con el otro sea negativo. Este método es conocido como interpolación.
3. Se resuelve la ecuación con tasas diferentes que la acerquen a cero.
- A. Se toma al azar una tasa de interés i = 3% y se reemplaza en la ecuación de valor.
-1.500.000 + 100.000 a12¬3% + 800.000 (1 +0.03)-1 = 56.504
- B. Ahora se toma una tasa de interés más alta para buscar un valor negativo y aproximarse al valor cero. En este caso tomemos i = 4% y se reemplaza con en la ecuación de valor
-1.500.000 + 100.000 a12¬4% + 800.000 (1 +0.04)-1 = -61.815
4. Ahora se sabe que el valor de la tasa de interés se encuentra entre los rangos del 3% y el 4%, se realiza entonces la interpolación matemática para hallar el valor que se busca.
- A. Si el 3% produce un valor del $56.504 y el 4% uno de – 61.815 la tasa de interés para cero se hallaría así:
- B. Se utiliza la proporción entre diferencias que se correspondan:
C. se despeja y calcula el valor para la tasa de interés, que en este caso sería i = 3.464%, que representaría la tasa efectiva mensual de retorno.
La TIR con reinversión es diferente en su concepción con referencia a la TIR de proyectos individuales, ya que mientras avanza el proyecto los desembolsos quedan reinvertidos a la tasa TIO
Evaluación de proyectos individuales con análisis de reinversión
Ejemplo
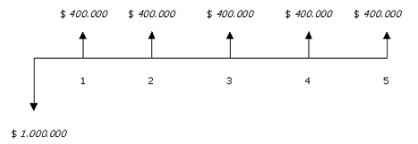
Una compañía le propone al gobierno construir un puente cuyo costo inicial es de $1.000.000 y necesita de $100.000 al final de cada año, como costos de mantenimiento y $500.000 por la cuota de amortización, con lo cual al final de este tiempo e puente será propiedad del estado. Si la TIO de la compañía es del 2.5% efectivo mensual, se pide determinar cuál es la verdadera rentabilidad del proyecto con reinversión de los dineros que va liberando el proyecto,
Solución
1. Se realiza la gráfica del problema
2. Puesto que los $500.000 y los $100.000 se encuentran enfrentados en el mismo periodo de tiempo la gráfica se podría simplificar a:
3. Teniendo claro lo anterior, se plantea y soluciona la ecuación de valor por medio de la metodología de la TIR
-1.000.000 + 400.000 a5¬i = 0
A. Se utiliza una tasa de interés i = 28%
-1.000.000 + 400.000 a5¬28% = 12.802
B. Se utiliza una tasa de interés i = 30 %
-1.000.000 + 400.000 a5¬30% = – 25.772
4. Se utiliza la interpolación matemática para hallar la tasa de interés que se busca.
5. Se utiliza la proporción entre diferencias que se correspondan:
Se tiene entonces que, la tasa de interés sería i = 28.664%, que representaría la tasa efectiva mensual de retorno.
Pero en este ejemplo también se debe tener en cuenta los desembolsos reinvertidos a la Tasa de Interés de Oportunidad (TIO) entonces, si la TIO de la compañía es del 2.5% se tiene que:
6. Al calcular las tasas equivalentes y despejando i
(1 +0.025)12 = (1 +i)1
La tasa de interés sería i = 34.489% efectivo anual.
Ahora analizando la TIR del proyecto sin reinversión es del 28.664% y la TIO es del 34.489%, se concluye que el proyecto sin reinversión de intereses no es recomendable; sin embargo, al incluir la inversión de intereses se debe tener en cuenta que el proyecto devuelve $400.000 al final de cada año los cuales podrían ser reinvertidos a la Tasa TIO. Por lo tanto habrá que calcular el valor final para esta serie de pagos anuales de $400.000 cada uno.
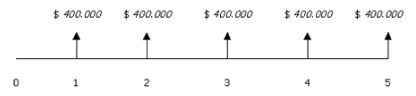
7. Se realiza la gráfica de la línea de tiempo.
8. Se calcula la ecuación de valor de la serie de pagos, pero ahora evaluada con la tasa i = 34.488%, para hallar el valor con reinversión de la TIO
400.000 s5¬34.488% = 3.943.055,86
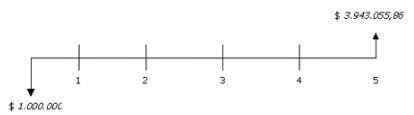
En conclusión $1.000.000 invertidos hoy en el puente se convertirán al final de cinco años con reinversión de intereses en $3.943.055,86, por lo tanto su verdadera rentabilidad sería:
9. Línea de tiempo
10. Al hallar la tasa de interés en la ecuación de valor se obtiene:
3.943.055,86 = 1.000.000 (1 +i)5
En este caso la i = 31.57 con reinversión.
Se observa entonces que la tasa de interés y por ende la rentabilidad total del proyecto con reinversión aumenta, pero esta no sobrepasa el 34.49% efectivo anual que es equivalente a la TIO del 2.5% efectivo mensual.
Cálculo de la tasa interna de retorno, por el método caue
Cuando se utiliza el Valor Presente Neto (VPN) para calcular la TIR debe hacerse tomando en cuenta el mínimo común múltiplo de los años de vida útil de cada alternativa, sin embargo, cuando se hace uso del CAUE, solo es necesario tomar en cuenta un ciclo de vida da cada alternativa, pues lo que importa en este caso es el costo de un año; esto puede hacer que en ocasiones sea de más fácil aplicación.
CAUE. El Costo Anual Unitario equivalente se utiliza en estos casos como soporte de las decisiones financieras
Ejemplo
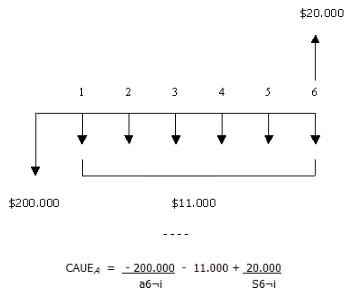
Una fábrica necesita adquirir una máquina, la Tasa Interna de retorno (TIR) es del 25%. Las alternativas de inversión se presentan a continuación:
| A | B | |
| Costo Inicial (C) | $200.000 | $180.000 |
| Costo Anual de Operación (CAO) | $11.000 | $10.500 |
| Valor de Salvamento (S) | $20.000 | $20.000 |
| Vida Útil (K) | 6 años | 4 años |
¿Cuál de las dos alternativas es más viable?
Solución
1. Se realiza la línea de tiempo para la alternativa A
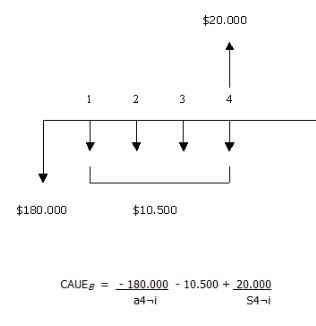
2. Se realiza la línea de tiempo para la alternativa B
3. Se resta la alternativa A y la B
4. Por interpolación matemática, se busca la tasa a la cual se cumplen las condiciones impuestas en la ecuación anterior. Interpolando entre el 25% y el 30% se tiene:
De donde se obtiene la Tasa de Interés i = 26.27%
Esto significa que el excedente de inversión
$200.000 – 180.000 = 20.000
Queda rentando el 26.27%, que es superior a la TIO; en consecuencia es aconsejable invertir en la máquina A. Si se hubiera obtenido un valor inferior al 25% entonces se hubiera recomendado la máquina B.
La utilización de la metodología matemática se basa en lo que podría suceder si se aplican reglas inequívocas, el riesgo es diferente para cada tipo de proyecto
Un par de videos para complementar, en el primero se explica qué es la tasa interna de retorno (TIR) y cómo se interpreta, en el segundo se ilustra, con bastante claridad, cómo calcularla.
Método de la tasa interna de retorno incremental (TIRI)
El método de la Tasa Interna de Retorno Incremental (TIRI) consiste en calcular la TIR a la cual se hace cero la ecuación de valor que se plantea por el método del Valor Presente Neto Incremental (VPNI). Así se debe entender que la TIRI es la tasa a la cual se invierte el capital adicional que se necesita, en caso de decidirse por la alternativa más costosa.
Ejemplo
Dadas las alternativas de inversión A, B y C, seleccionar la más conveniente suponiendo una tasa del 20%.
| Alternativas de inversión | A | B | C |
| Costo inicial | -100.000 | -120.000 | -125.000 |
| Costa anual de operación Año 1 | -10.000 | -12.000 | -2.000 |
| Costa anual de operación Año 2 | -12.000 | -2.000 | -1.000 |
| Costa anual de operación Año 3 | -14.000 | -2.000 | 0 |
1. Primero se compara la alternativa A con la B
| Alternativas de inversión | A | B | B-A |
| Costo inicial | -100.000 | -120.000 | -20.000 |
| Costa anual de operación Año 1 | -10.000 | -12.000 | -2.000 |
| Costa anual de operación Año 2 | -12.000 | -2.000 | +10.000 |
| Costa anual de operación Año 3 | -14.000 | -2.000 | +12.000 |
2. Se calcula en la ecuación de Valor Presente Neto Incremental (VPNI) igualada a cero la Tasa de Interés.
VPNI -20.000 – 2.000 (1+i)-1 + 10.000 (1+i)-2 + 12.000 (1+i)-3 = 0
Se deduce entonces, que el exceso de inversión, en este caso $20.000, están ganando una tasa del 0% que no es atractiva, en consecuencia es mejor la alternativa A.
3. Al comprobar que la alternativa A es mejor, se compara ahora con la alternativa C.
| Alternativas de inversión | A | C | C-A |
| Costo inicial | -100.000 | -125.000 | -25.000 |
| Costa anual de operación Año 1 | -10.000 | -2.000 | +8.000 |
| Costa anual de operación Año 2 | -12.000 | -1.000 | +11.000 |
| Costa anual de operación Año 3 | -14.000 | 0 | +14.000 |
VPNI -25.000 + 8.000 (1+i)-1 + 11.000 (1+i)-2 + 14.000 (1+i)-3 = 0
4. Se Interpola matemáticamente:
De donde se obtiene que i = 13.855%,
Lo cual significa que $25.000 que corresponde al exceso de inversión quedan colocados al 13.855%, por lo tanto, se concluye que la alternativa no es aconsejable, porque la tasa mínima a la cual se debe invertir es el 20%.
Análisis beneficio/costo
Las entidades crediticias internacionales acostumbran a evaluar proyectos y es casi una exigencia que un proyecto con financiación del exterior sea evaluado con el método del Beneficio/Costo
Método de la relación beneficio/costo (b/c)
La relación Beneficio/costo está representada por la relación
Ingresos / egresos
En donde los Ingresos y los Egresos deben ser calculados utilizando el VPN o el CAUE, de acuerdo al flujo de caja; pero, en su defecto, una tasa un poco más baja, que se denomina «TASA SOCIAL» ; esta tasa es la que utilizan los gobiernos para evaluar proyectos.
El análisis de la relación B/C, toma valores mayores, menores o iguales a 1, lo que implica que:
- B/C > 1 implica que los ingresos son mayores que los egresos, entonces el proyecto es aconsejable.
- B/C = 1 implica que los ingresos son iguales que los egresos, entonces el proyecto es indiferente.
- B/C < 1 implica que los ingresos son menores que los egresos, entonces el proyecto no es aconsejable.
Alternativas. Esta metodología permite también evaluar dos alternativas de inversión de forma simultánea
Al aplicar la relación Beneficio/Costo, es importante determinar las cantidades que constituyen los Ingresos llamados «Beneficios» y qué cantidades constituyen los Egresos llamados «Costos«.
Por lo general, las grandes obras producen un beneficio al público, pero a su vez, produce también una perdida denominada «Desventaja«, se puede tomar como ejemplo de esto la construcción de una represa hidroeléctrica, la cual produce un beneficio que es la generación de electricidad. La electricidad puede ser cuantificada en dinero; a su vez, se produce una pérdida, por la inundación de terrenos aptos para la agricultura y esa pérdida, también puede ser cuantificada en dinero.
Para que las decisiones tomadas sean correctas, cuando se utiliza la relación B/C es necesario aplicar en las cálculos la TIO.
Ejemplo 1
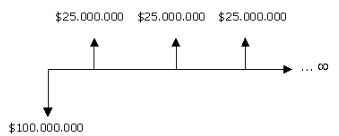
El costo de una carretera alterna a la principal es de $100.000.000 y producirá un ahorro en combustible para los vehículos de $2.000.000 al año; por otra parte, se incrementará el turismo, estimado el aumento de ganancias en los hoteles, restaurantes y otros en $28.000.000 al año. Pero los agricultores se quejan porque van a tener unas pérdidas en la producción estimadas de unos $5.000.000 al año. Utilizando una tasa del 22%, ¿Es aconsejable realizar el proyecto?
Solución
1. Si se utiliza el método CAUE para obtener los beneficios netos, se debe analizar la ganancia por turismo es una ventaja, al igual que el ahorro de combustible, pero las pérdidas en agricultura son una desventaja. Por lo tanto, los beneficios netos serán:
Beneficios netos = $28.000.000 + 2.000.000 – 5.000.000
Beneficios netos = $25.000.000
2. Ahora se procede a obtener el costo anual, dividiendo los $100.000.000 en una serie infinita de pagos:
Anualidad = R / i
R = A. i
R = 100.000.000 * 0.22
R = 22.000.000
3. Entonces la relación Beneficio/Costo estaría dada por:
B/C = 25.000.000 / 22.000.000
B/C = 1,13
El resultado es mayor que 1, por eso el proyecto es aceptado.
1. Por el método de VPN este problema se soluciona así:
2. Se calcula el VPN
VPN Ingresos = 113.636.364
VPN Egresos = 100.000.000
3. Entonces se tiene:
Como puede verse, por este método el resultado es igual, por ello el proyecto es aceptado por que el resultado obtenido es mayor que 1.
En el análisis Beneficio/Costo se debe tener en cuenta tanto los beneficios como las desventajas de aceptar o no un proyecto de inversión
Ejemplo 2
Se está pensando en la construcción de un terminal de transportes y se han considerado dos tipos de estructuras, el tipo A tiene un costo inicial de $100.000.000, el costo anual de operación y mantenimiento de equipos, para el primer año será de $5.000.000 y cada año aumentará en un 10%. Además, será necesario una inversión adicional de $20.000.000, cada 10 años, para remodelaciones y reacondicionamiento; tendrá una vida útil de 40 años y un valor de salvamento de $30.000.000. El tipo B tiene un costo de $43.000.000; el costo anual de operación para el primer año será de $2.000.000 y cada año, aumentará en un 12%. Cada 5 años deberá invertirse $10.000.000 en remodelaciones y reacondicionamiento, tendrá una vida útil de 40 años y un valor de salvamento de $25.000.000.
La estructura A, por ser más grande, permite la instalación de más empresas transportadoras y más almacenes, por lo tanto se estima que la diferencia de ganancias a favor de la estructura A será de $600.000 en el primer año y cada año, se estima que aumentará en $300.000 hasta el año 25. A partir de ese momento, permanecerá constante hasta el final de su vida útil. Si suponemos una TIO del 20%, determinar por el método del B/C cuál es la estructura que se debe realizar.
Solución
1. Primero se debe calcular la diferencia de beneficio, a partir del año 25. Como los beneficios forman un gradiente lineal se tiene que:
R25 = R1 + L ( n – 1 )
R25 = 600.000 + 300.000 (25 – 1 )
R25 = 7.800.000
2. El método más sencillo para hallar la relación B/C es por medio de la CAUE, entonces:
VP = 600.000 a25¬20% + 300.000/0.2 [ a25¬20% – 25(1 +0.2)-25] + 7.800.000 a15¬20% (1+0.2)-25
VP = 2.968.552 + 7.028.283 + 382.287
VP = $10.379.122
3. Ahora se divide el VP entre 40 pagos anuales uniformes así:
CAUE = 10.379.122 / a40¬20%
CAUE = 2.077.238
Como ya se ha encontrado el CAUE de la diferencia de beneficios, se tendrá que hallar ahora el CAUE de la diferencia de costos; entonces se empieza a analizar los costos de la estructura B.
4. Se calcula el CAUE del costo inicial:
CAUE = 100.000.000 / a40¬20%
CAUE = 20.013.617
5. Luego se halla el CAUE del costo anual de operación:
CAUE = 5.000.000[ (1 +0.1)40 (1 +0.2)-40 – 1] /0.1 – 0.2 / a40¬20%
CAUE = 9.698.665
6. Se calcula el CAUE de la inversión adicional:
CAUE = 20.000.000 / S10¬20%
CAUE = 770.445
7. Ahora se calcula el CAUE de salvamento
CAUE = 30.000.000 / S40¬20%
CAUE =4.085
8. Entonces el CAUE de la estructura B será:
CAUEB = 20.013.617 + 9.698.665 + 770.445 – 4.085
CAUEB =30.478.652
Ahora se calcula el CAUE de la estructura A.
9. Se calcula el CAUE del costo inicial:
CAUE = 43.000.000 / a40¬20%
CAUE = 8.605.855
10. Luego se halla el CAUE del costo anual de operación:
CAUE = 2.000.000[ (1 +0.12)40 (1 +0.2)-40 – 1] /0.12 – 0.2 / a40¬20%
CAUE = 4.686.640
11. Se calcula el CAUE de la inversión adicional:
CAUE = 10.000.000 / S5¬20%
CAUE = 1.343.797
12. Ahora se calcula el CAUE de salvamento
CAUE = 25.000.000 / S40¬20%
CAUE = 3.404
13. Entonces el CAUE de la estructura A será:
CAUEA = 8.605.855 + 4.686.640 + 1.343.797 – 3.404
CAUEA =14.632.888
14. Ahora se calcula la diferencia entre el proyecto A y el B
CAUEB – CAUEA= 30.478.652 – 14.632.888
CAUEB – CAUEA = 15.845.764
15. La relación Beneficio/Costo será:
B/C = 2.077.238/15.845.765
B/C = 0.131
El valor hallado es menor que 1, esto significa que el incremento de inversión no se justifica, por lo tanto, se decide por la estructura A.
El análisis que se realiza en la evaluación de un proyecto puede que no sea la más adecuada en el momento de tomar decisiones frente a un desembolso de efectivo
Método período de recuperación ( PR)
La metodología del Periodo de Recuperación (PR), es otro índice utilizado para medir la viabilidad de un proyecto, que ha venido en cuestionamiento o en baja. La medición y análisis de este le puede dar a las empresas el punto de partida para cambias sus estrategias de inversión frente al VPN y a la TIR.
El Método Periodo de Recuperación basa sus fundamentos en la cantidad de tiempo que debe utilizarse, para recuperar la inversión, sin tener en cuenta los intereses. Es decir, que si un proyecto tiene un costo total y por su implementación se espera obtener un ingreso futuro, en cuanto tiempo se recuperará la inversión inicial.
Efectos fiscales. En la evaluación de cualquier proyecto de inversión se deben tener en cuenta las erogaciones que se deben realizar por las tasas impositivas
Al realizar o invertir en cualquier proyecto, lo primero que se espera es obtener un beneficio o unas utilidades, en segundo lugar, se busca que esas utilidades lleguen a manos del inversionista lo más rápido que sea posible, este tiempo es por supuesto determinado por los inversionistas, ya que no es lo mismo para unos, recibirlos en un corto, mediano o largo plazo, es por ello que dependiendo del tiempo es aceptado o rechazado.
Ejemplo
Un inversionista pretende comparar dos proyectos para saber en cuál invertir su dinero. Realizar una analogía entre el Método Periodo de Recuperación y el VPN con una tasa de interés del 20%
| PROYECTO | A | B |
| Inversión Inicial | $600.000 | $600.000 |
| Retorno año 1 | $300.000 | $100.000 |
| Retorno año 2 | $300.000 | $200.000 |
| Retorno año 3 | $100.000 | $300.000 |
| Retorno año 4 | $50.000 | $400.000 |
| Retorno año 5 | $0 | $500.000 |
Solución
1. Por el Método de Periodo de Recuperación se aprecia en la tabla que en el proyecto A, se recuperaría la inversión inicial en 2 años y en el proyecto B en 3 años, en consecuencia la alternativa A será la escogida.
2. Por el VPN al 20 % se tiene que
a) Para el proyecto A el VPN es igual a:
VPN(A)= – 600.000 +300.000(1+0.2)-1+ 300.000(1+0.2)-2 +100.000(1+0.2)-3 + 50.000(1+0.2)-4
VPN(A)= – 59.684
b) Para el proyecto B el VPN es igual a:
VPN(B)= – 600.000 +100.000 a5¬20% + 100.000/0.2 [a5¬20% – 5 (1 + 0.2)-5]
VPN(B)= 189.673
Nos damos cuenta que por el Método del Valor Presente Neto (VPN), el proyecto sería rechazado y el B sería el que acogería el inversor. Esta diferencia en los resultados se da por que la aplicar el Método Periodo de Recuperación, el análisis en la evaluación de proyectos, se presentan fallas técnicas inherentes al modelo, entre las cuales sobresalen la de no tomar en cuenta el valor del dinero a través del tiempo y la de no tener en cuenta el flujo de caja, después de la recuperación del dinero invertido.
La metodología de Periodo de Recuperación es utilizada por muchas empresas a pesar de sus problemas, ya que para ellos el flujo de caja en el largo plazo es incierto
Método del costo capitalizado (CC)
El Método del Costo Capitalizado se presenta como una aplicación del Valor Presente de una Anualidad Infinita. Este es aplicado en proyectos que se supone tendrán una vida útil indefinida, tales como represas, universidades, organizaciones no gubernamentales, etc. También, es aplicable en proyectos que deben asegurar una producción continua, en los cuales los activos deben ser reemplazados periódicamente.
Para realizar un análisis sobre esta metodología, se debe hallar el Valor Presente de todos los gastos no recurrentes y sumarlos con el Valor Presente de la Anualidad Infinita, que conforman dichos gastos.
Ejemplo
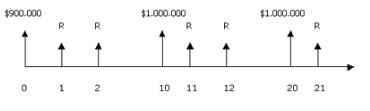
Un industrial tiene dos alternativas para comprar una máquina. La primera máquina se la ofrecen con un costo inicial de $900.000 y tiene una vida útil de 10 años, al final de los cuales deberá ser reemplazada a un costo de $1.000.000. La segunda máquina la ofrecen a un costo de $1.000.000; su vida útil es de 15 años y su costo de reemplazo es de $1.500.000. Si se supone que el interés efectivo es del 20%. ¿Cuál máquina debe comprar?
Solución
1. Como la primera máquina debe ser reemplazada cada 10 años, debe constituirse un fondo, mediante pagos anuales $R, con el objeto de tener disponibles $1.000.000 al final del periodo, para efectuar el reemplazo, se tiene entonces que la gráfica de tiempo sería:
1.1. Se halla el valor de los pagos:
1.000.000 = R S10¬20%
R = 38.523
1.2. El Valor Presente de la renta perpetua será:
Anualidad (A) = R / i
Anualidad (A) = 38.523/ 0.2
Anualidad (A) = 192.614
1.3. Los costos no recurrentes son $900.000, que están en valor presente, por lo tanto el costo capitalizado es:
CC = 900.000 + 192614
CC = 1.092.614
2. La segunda máquina debe ser reemplazada cada 15 años, también debe constituirse un fondo, mediante pagos anuales $R, para tener el dinero necesario de $1.500.000 al final del periodo, para efectuar el reemplazo, se tiene entonces que la gráfica de tiempo sería:
2.1. Se halla el valor de los pagos:
1.500.000 = R S15¬20%
R = 20.823
2.2. El Valor Presente de la renta perpetua será:
Anualidad (A) = R / i
Anualidad (A) = 20.823 / 0.2
Anualidad (A) = 104.115
2.3. Los costos no recurrentes son $1.000.000, que están en valor presente, por lo tanto el costo capitalizado es:
CC = 1.000.000 + 104.115
CC = 1.104.115
La decisión que se tomaría sería por la primera máquina, que es la que tiene el menor costo capitalizado.