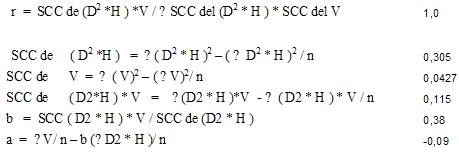Como tema de mayor importancia, la formación de tablas de cubicación toma como función el volumen maderable, de modo que el colectivo principal está formado por fustes.
Introducción
En la expresión del volumen individual se consideran como argumentos tabulares los siguientes parámetros: el diámetro normal con corteza, la altura del fuste hasta el diámetro de 7cm, y el coeficiente mórfico, todas contenidas en la formula de cota.
Según que parámetros se incluyan, las tablas pueden ser de tres tipos.
- Tablas locales: V = f (DAP)
- Tablas normales: V = f (DAP, h )
- Tablas generales: V = f (DAP, h, di )
En el primer caso la tabla posee una sola entrada. El DAP, lo que supone una homogeneidad de la población en cuanto a su altura para cada clase día métrico. Por ello su aplicación está restringida a ciertas áreas definidas, con plantaciones comerciales de tratamiento silvícola similar; es decir, son de uso local.
En el segundo caso, las longitudes de fustes varían en tal grado que no se admite su representación por un promedio para cada clase o valor. Por lo tanto, el volumen deberá estar representado por dos parámetros: el DAP y la altura. Se entiende que estas tablas son aplicables a una diversidad de situaciones y extensiones, es decir, son uso normal.
Las tablas generales se usan en inventarios nacionales europeos, con una variedad enorme de sitios y tratamientos silvícola. Tienen como entrada el DAP, la altura total y un segundo diámetro más arriba, generalmente a 5 o 7 m de altura.
Cuando se usan tablas y hay valores de los parámetros que no figuran ( por ejemplo , mediciones en milímetros) , se debe interpolar entre los dos más próximos. Si DAP o la altura es mayor que el límite de la tabla, se extrapola.
Tanto en las tablas locales como en las normales el coeficiente mórfico está implícito en los argumentos de entrada.
Por ejemplo, si tenemos la altura y el volumen y nos falta el DAP, mediante la tabla podemos determinar el DAP multiplicando por f.
Análogamente, con la altura obtendremos la altura reducida f. h. a las tablas de cubicación se las utiliza no solo para cálculo de los volúmenes individuales sino también para determinar el volumen de los rodales según diferentes métodos.
Funciones de volumen
Los volúmenes de los árboles pueden determinarse fácilmente mediante funciones de volumen o funciones de coeficiente mórfico.
Existen una gran variedad de funciones que describen el volumen, y su forma varia con el grado de precisión que se desee. Algunos ejemplos para tablas de 1, 2 ,3 entradas, respectivamente.
Ecuación de una variable
Representa una función que produce estimaciones de volumen en función de D, al igual que las tablas de una entrada, son aptas para localidades donde la calidad de sitio es homogénea y las diferencias de altura dentro de las mismas edades es pequeña.
Tabla de volumen de una entrada
1) V = a * Db
2) V = a + b*D2
3) V = a + bD + c*D2
Ecuación de dos variables
Tablas de volumen de doble entrada
1) V = a + b (D*H)
2) V = a + b (D2 * H)
3) V = a*D*H
Ecuación de tres variables
Tablas de volumen de triple entrada
V = f (b * H *D)
V = f (D1:30 * D1/2 *H)
Pasos necesarios para la construcción de tabla de volumen
1: calcular el volumen en trosas empleando diferentes métodos para el cálculo de volúmenes, como Huber, Smalian, Newton……..etc.
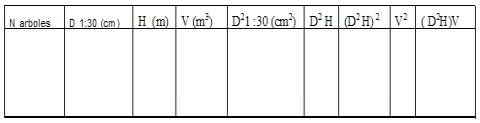
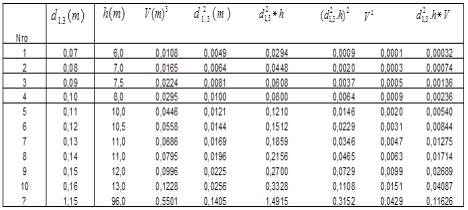
2: Organizar los datos y hacer los cálculos correspondiente mediante los siguiente tabla.
3: calcular los términos de corrección (TC)
a) TC para ∑( D2*H )2 = ∑(D2* H )2/ n
b) TC para ∑ V2 = ( ∑V )2 / n
c) TC para ∑(D2 * H )*V = ∑( D2 *H ) * ( ∑V ) / n
4: calcular la suma de los cuadrados corregidos (SCC)
a) SCC de ( D2 *H ) = ∑( D2 * H )2 – ( ∑ D2 * H )2 / n
b) SCC de V = ∑ ( V)2 – ( ∑V)2/ n
c) SCC de ( D2*H ) * V = ∑(D2 * H )*V – ∑ ( D2 * H ) *∑ V / n
5: calcular el coeficiente de regresión (b)
V = a + b (D2 *H) de doble entrada.
b = SCC (D2 * H) * V / SCC de (D2 * H)
6: calcular la constante (a)
a = ∑V/ n – b (∑D2 * H)/ n
7: sustituir los valores de (a), (b) en la ecuación
V = a + b ( D2 *H ) de doble entrada.
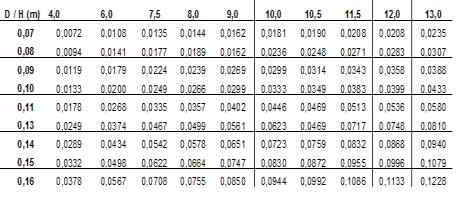
8: construir la tabla
V = a + b ( D2 *H ) de doble entrada.
D/H
D: diámetro
H: altura
Para construir la tabla se debe utilizar cada diámetro correspondiente a cada altura.
Y sustituir en la ecuación de volumen.
9: determinación de la precisión para este cálculo.
Cuando:
r =0,96 – 1 dentro de este intervalo se acepta la tabla.
r = SCC de (D2 *H) *V / √ SCC del (D2 * H) * SCC del V
La tabla de volumen debe de ir acompañado de una serie de informaciones como:
- El titulo de la tabla.
- Donde se elaboro la tabla.
- Entrada
- Descripción ecológica de la especie donde se elaboro la tabla.
- Características dendrologicas de la especie y del fuste.
- Procedimiento seguido.
- La formula que se empleo para el cálculo de volumen.
Ejemplo
Construcción de tabla de volumen
El modelo de dos entradas:
V = a + b (D2 *H) de doble entrada.
Formula utilizado para el cálculo de volumen Newton.
V = a + b (D2 *H) de doble entrada estudiante
Tabla de volumen