Modelos económico-matemáticos en la decisión empresarial

Continuamente, las personas deben elegir entre varias opciones aquella que consideran más conveniente. Es decir, han de tomar gran cantidad de decisiones en su vida cotidiana, en mayor o menor grado importantes, a la vez que fáciles o difíciles de adoptar en función de las consecuencias o resultados derivados de cada una de ellas.

El estudio de la toma de decisiones presupone ser lógicos, racionales y objetivos al resolver problemas, de ahí que se utilicen diferentes modelos matemáticos y econométricos que al constituir el lenguaje del pensamiento racional permiten expresar pensamientos complejos de manera concisa.

Los directivos y profesionales en general en su desempeño laboral necesitan de herramientas que le permitan tomar decisiones de forma eficiente y fundamentada científicamente. Hoy en día los métodos cuantitativos en administración pueden llamarse de varias maneras: investigación de operaciones, ciencias de la administración, análisis de sistemas, análisis costo beneficio, estadística, econometría y otros. De cualquier manera, la esencia es la misma: ser racional y científico al tomar una decisión empresarial.

Estos elementos de modelación matemática están indisolublemente unidos a lo que hoy se conoce como Métodos económicos matemáticos para la toma de decisiones, los cuales desarrollan modelos de optimización que permiten describir sistemas de producción y servicio y analizar estrategias óptimas considerando entre otros elementos la disponibilidad de recursos, condiciones de mercado, de insumos y productos, eficiencia productiva, manejo y estructura de la organización, estructura de costos y precios, niveles de producción y uso de tecnología.

Deben tenerse varios factores en mente al seleccionar qué método cuantitativo se va a aplicar. Además de las consideraciones de beneficio/costo, es necesario pensar en cuáles son los métodos con que el analista y el usuario se sienten a gusto, en el tipo de situación que se va a analizar, en la cantidad de poder descriptivo requerida, en la cantidad de tiempo disponible para el desarrollo del modelo y en la disponibilidad de datos.

Las organizaciones cubanas, en particular, debido a la urgente revitalización económica a la que está obligado el país, encaran nuevas metas: resistir, sobrevivir y ser competitivo en el nuevo entorno. Para ello, deben elevar sus niveles de productividad, eficiencia y rentabilidad por lo que sus miembros se cuestionan si sus empresas están preparadas para afrontar estas metas en las nuevas condiciones, reflexión que los conduce al análisis y revisión de las mismas. De ahí la importancia de aplicar métodos económicos – matemáticos que permitan tomar decisiones en cualquier área de la empresa.

Para contrarrestar los efectos de las condiciones internas y externas existentes, la dirección política de Cuba ha tenido que trazar un conjunto de acciones y medidas que propicien sustentar la economía en condiciones de eficiencia en aras de garantizar la continuidad y el desarrollo prospectivo de la Revolución y la preservación de su esencia socialista.

De ahí que todo un andamiaje de transformaciones a partir de lo establecido en el VI Congreso del Partido Comunista de Cuba se abre camino a los objetivos empresariales de desarrollarse y trae consigo la necesidad de decidir en todo momento sobre la utilización eficiente de los recursos de los que se dispone, para lograr mayor economía, eficiencia y eficacia en todos sus procesos. Al estudiar los Lineamientos de la Política Económica y Social del Partido y la Revolución en su capítulo I Modelo de gestión económica se enuncia en el Lineamiento 8 que “El incremento de facultades a las direcciones de las entidades estará asociado a la elevación de su responsabilidad sobre la eficiencia, eficacia y el control en el empleo del personal, los recursos materiales y financieros que manejan; unido a la necesidad de exigir la responsabilidad a aquellos directivos que con decisiones, acciones u omisiones ocasionen daños y perjuicios a la economía”.

Partiendo de este punto es que la economía cubana está viviendo un período de fuertes modificaciones, lo que hace que la dirección del país y el gobierno, centre sus esperanzas futuras en una excelente gestión empresarial, donde sin lugar a dudas el proceso de toma de decisiones fundamentadas en los modelos económicos – matemáticos existentes tiene un papel importante.

Teniendo en cuenta lo anteriormente expresado se plantea como objetivo de esta investigación: Ejemplificar los métodos económicos – matemáticos para la toma de decisiones partiendo de los conceptos básicos de la teoría de la decisión.

Para la realización de este estudio investigativo se emplearon como métodos y técnicas de investigación las siguientes:

Métodos del nivel teórico

Histórico-Lógico. Para determinar los antecedentes y necesidad de la toma de decisiones y de los modelos económicos – matemáticos.
Análisis-Síntesis: Para la caracterización gnoseológica y metodológica de la toma de decisiones y de los modelos económicos – matemáticos.
Hipotético-Deductivo: Desarrollo de una idea de hacia donde va dirigida la investigación según el análisis realizado de la bibliografía consultada y sintetizada.
Abstracción-Concreción: En la aplicación de los modelos y métodos para la toma de decisiones en los ejemplos presentados.

Enfoque en Sistema: Permite estudiar la integración de los modelos econométricos al proceso de toma de decisiones.

El trabajo está estructurado para un mayor entendimiento en: Introducción, Desarrollo, Conclusiones, Bibliografía y Anexos.

DESARROLLO

Modelos de criterios para la Toma de Decisiones.

Para entender claramente los modelos que se utilizan en la toma de decisiones es necesario comentar el concepto de modelo matemático y su utilización en la economía como elemento fundamental dentro de la toma de decisiones a partir de los elementos que conforman la teoría de la decisión.

Modelos matemáticos aplicados a la economía.

Para adoptar algunos tipos de decisiones se suelen utilizar modelos, ya que existen causas que incrementan la complejidad de los problemas en la cotidianidad empresarial como son:

La presencia de un número considerable de variables.
Que en el problema no sólo interviene un individuo, sino un grupo o varios.
Que el problema esté sujeto a una alta dinámica de cambios.
Que sean muchas las alternativas.

Se pueden resolver los problemas sencillos y complicados del mundo real si nos concentramos en la situación global o en alguna porción o características principales, y no en cada detalle. Esa aproximación o extracción de la realidad, que puede crearse de varios modos, se llama modelo, y por lo general se presenta por ecuaciones algebraicas.

Existen varias definiciones de «modelo», podemos asumir la siguiente «sistema representado en la mente o en la realidad, el cual se encuentra en determinadas relaciones con otro sistema (el original)» (Morales Pita, 1984).

A su vez puede decirse que la modelación matemática «es el proceso de imitar la realidad utilizando el lenguaje de las matemáticas» (Kent y Saft, 1992), este lenguaje es lo suficientemente rico como para tratar los más diversos problemas tanto por la materia de su contenido como por su complejidad.

Los modelos matemáticos se corresponden con los llamados modelos formales donde el sistema económico en estudio se describe en su mayoría a través de ecuaciones e inecuaciones que expresan relaciones funcionales que contienen variables, las cuales, por su esencia, pueden ser de dos tipos: controlables o de decisión (representan aspectos o elementos del sistema modelado que pueden ser afectados por el hombre) y no controlables (aquellas sobre las cuales el hombre no puede ejercer acción). Si además el objetivo económico forma parte del modelo, se tiene un modelo de optimización.

La modelación matemática tiene como objetivo principal el asegurar una modelación altamente calificada de los procesos y fenómenos económicos, para después con la técnica matemática más apropiada realizar la elaboración racional de la información existente para la dirección y la planificación. Efectuar el análisis cuantitativo, es decir, determinar los valores óptimos de las variables controlables de acuerdo con algún criterio de evaluación (técnicas de optimización), o estudiar el efecto que sobre el comportamiento del fenómeno pueden tener diferentes conjuntos de valores de las variables. Esto permite asegurar la toma de las decisiones más racionales para el desarrollo de la organización y la elevación de su efectividad.

Las técnicas de la modelación matemática se dividen en:

Deterministas: son aquellos en los cuales las variables no son aleatorias y las relaciones entre ellas son exactas y bien definidas. Ejemplos: Programación Lineal, Transporte y Asignación, Teoría de Redes y Grafos y la Programación Dinámica.
Estocásticas (probabilísticas): intervienen variables aleatorias, ya sean discretas o continuas sujetas a una distribución de probabilidad al menos una de ellas. Se apoyan en la Teoría de Colas, Teoría de Inventarios, Simulación, Procesos de Markov y otros.

Todas las técnicas para adoptar decisiones comprenden unos elementos comunes que permiten mostrar de forma cuantitativa la valoración en términos de beneficios y/o pérdidas de las diferentes opciones que se presentan.

Las ventajas de contar con un modelo sencillo son:

Requieren buena comprensión del problema.
Necesitan el reconocimiento de todas las variables (controlables y no controlables) relevantes.
Facilitan la comprensión de las relaciones, los costos y las negociaciones existentes entre las variables.
Permiten manipular las variables y realizar las pruebas de cursos alternativos de acción.
La economía de la representación.
Los modelos permiten analizar y experimentar situaciones complejas hasta un grado que sería imposible si se construye el sistema en la realidad.
Reducir la cantidad de tiempo y esfuerzo.
El que decide puede comprenderlo rápidamente.
Si es necesario, el modelo se puede modificar de manera rápida y efectiva.

El objetivo del decisor no es construir un modelo que sea lo más parecido posible a la realidad, se busca el modelo más sencillo que pronostique los resultados con precisión razonable y que sea consistente con la acción efectiva.

El principal objetivo de un modelo es permitir una mejor comprensión y descripción de la parte de la realidad que representa, lo que permitirá tomar mejores decisiones. Los modelos se pueden clasificar atendiendo a numerosos criterios entre ellos:

Modelos objetivos y subjetivos. En ocasiones los sucesos no se pueden experimentar objetivamente, y no existen métodos formales para su estudio, por lo que los modelos han de ser informales, subjetivos y basarse en la intuición.
Modelos analíticos y de simulación. Los modelos analíticos son aquellos que sirven para obtener soluciones, por lo tanto han de ser resueltos. Los modelos de simulación son representaciones simplificadas de la realidad sobre las que se opera para estudiar los efectos de las distintas alternativas de actuación.
Modelos estáticos y dinámicos. Los modelos estáticos son aquellos que no utilizan la variable tiempo, en tanto que los dinámicos son aquellos que incorporan el tiempo como variable o como parámetro fundamental.
Modelos deterministas y probabilísticos. En los modelos deterministas se suponen conocidos con certeza todos los datos de la realidad que representan. Si uno o varios datos se conocen sólo en términos de probabilidades, el modelo se denomina probabilístico, aleatorio o estocástico.

Generalizando los Métodos Cuantitativos no es más que la aplicación del método científico por un grupo multidisciplinario de personas a un problema, principalmente relacionado con la distribución eficaz de recursos limitados (dinero, materia prima, mano de obra, energía), que se apoya en el enfoque de sistemas (este enfoque, es aquel en el que un grupo de personas con distintas áreas de conocimiento, discuten sobre la manera de resolver un problema en grupo). Puede considerarse tanto un arte como una ciencia. Como arte refleja los conceptos eficiente y limitado de un modelo matemático definido para una situación dada. Como ciencia comprende la deducción de métodos de cálculo para resolver los modelos.

A su vez los Métodos Cuantitativos, como expresión general, se emplean de tres maneras:

Como guía en la toma de decisiones: Esta aplicación es la más extensa pero la menos tangible. Al aprender los métodos y modelos para manejar los problemas administrativos en forma cuantitativa, se gana práctica y experiencia en el pensamiento racional. El conocimiento de los métodos cuantitativos ayudará a guiar el pensamiento aun cuando nunca se haya escrito una ecuación.
Como ayuda en la toma de decisiones: Esta aplicación coadyuva en el proceso de toma de decisiones. Muchas veces no existirá un modelo para dar una solución, pero puede haber información útil que se puede obtener cuantitativamente
Para automatizar la toma decisiones: Esta aplicación es la más sencilla y la más impresionante. Si se puede modelar con exactitud un problema específico, entonces se puede desarrollar una fórmula o un conjunto de fórmulas para su solución. Si el problema no cambia, las fórmulas permanecen válidas y pueden programarse en una computadora. La computadora entonces toma la decisión.

Los Modelos Cuantitativos están diseñados para ayudar a la toma de decisiones administrativas, proporcionan un método objetivo y lógico para analizar los sistemas administrativos en un esfuerzo que posibilite tomar las decisiones óptimas. Con frecuencia emplearlos resulta menos costoso, más sencillo y más seguro que hacer pruebas en su equivalente real. Sin embargo, estas ventajas significativas no se obtienen sin limitaciones.

Estos elementos de modelación matemática están indisolublemente unidos a lo que hoy se conoce como Métodos económicos matemáticos para la toma de decisiones, los que juegan un papel importante en la administración, es decir, que son técnicas matemáticas que se utilizan con el objetivo de desarrollar y evaluar soluciones a problemas económicos, que sirvan de apoyo cuantitativo en la toma de decisiones, siendo la esencia de este proceso científico.

Los modelos se pueden representar de varias maneras. En el caso de problemas sencillos y repetitivos, todo el proceso de toma de decisiones puede ocurrir en la mente del que está decidiendo, quizás de manera informal e intuitiva. Si el problema es menos común o más complejo, pensamos un poco más acerca de él.

La técnica apropiada para describir y relacionar las variables seleccionadas depende en gran medida de la naturaleza de las variables, por lo que es necesario distinguir las bases cuantitativas y cualitativas para la toma de decisiones.

La gama de técnicas se extiende desde las corazonadas en un extremo hasta los análisis matemáticos complejos en el extremo opuesto.

Desde el punto de vista práctico no existe ni una técnica mejor ni una combinación que deba utilizarse en todas las circunstancia. La selección es individual y por lo general está dictada por los antecedentes y conocimientos del decisor y por los recursos disponibles.

Bases cualitativas: estos medios son útiles, no solo para los problemas que se refieren a los objetivos, sino también para los problemas que tratan con los medios de alcanzar los objetivos. En su aplicación son en alto grado personales, ampliamente conocidas y están consideradas por muchos como la manera natural de tomar una decisión; existen cuatro bases: intuición, hechos, experiencias y opiniones consideradas.
Bases cuantitativas: esta es la habilidad de emplear técnicas presentadas como métodos cuantitativos o investigación de operaciones, como pueden ser la programación lineal, teoría de líneas de espera y modelos de inventarios. Esta herramienta ayuda a los mandos a tomar decisiones efectivas, pero es muy importante no olvidar que las habilidades cuantitativas no deben, ni pueden reemplazar al buen juicio, en el proceso de la toma de decisiones.

Si se pueden medir de alguna forma y, sobre todo, si se les puede dar una representación cuantitativa, hay fuertes razones para usar una representación matemática del modelo, combinándola con los sistemas computarizados, de forma tal que se puedan manejar problemas que requieren modelos de gran complejidad, siendo más sencillo el proceso de toma de decisiones cuando puede aplicarse este análisis, el cual se ha extendido a otras áreas de las operaciones de la empresa y se ha establecido como una manera eficaz de atacar ciertos problemas de decisiones empresariales. Los directores actuales tienen que conocer estas técnicas y estos modelos tan bien como conocen los informes de contabilidad.

Hay que hacer una advertencia: los ejecutivos de una empresa nunca deberán ser prisioneros de un modelo cuantitativo ni aceptar automáticamente sus conclusiones como si fuera la decisión correcta. La conclusión que se obtiene de un modelo contiene cierto grado de error debido al proceso de abstracción. Es cuestión de juicio determinar cuándo es tan grande el error que hay que modificar la conclusión antes de aceptarla como solución. La cuantificación es un auxiliar del juicio empresarial, no un sustituto. Al considerar el análisis cuantitativo de problemas empresariales es deseable usar el mismo grado de escepticismo constructivo que se aplica a otros procesos de toma de decisiones.

Teniendo en cuenta estos elementos se debe hallar un equilibrio adecuado entre los factores cualitativos y los cuantitativos.

Concepto de decisión.

López y Martínez (2005) entienden por «decisión» suponer una «elección» o «selección» fundamentada en criterios de algún carácter bien establecido; es decir, «decisión» va a suponer una elección de acuerdo con un cuerpo de criterios que contemple, no solo el conocimiento previo de la gama de opciones, sino además una evaluación de los resultados posibles y la existencia de un ente decisor. Ello a su vez entraña que las condiciones de adopción de decisiones pueden dar origen a formulaciones claramente diferenciadas, por lo que debemos tener claros los elementos que componen una situación de decisión, detallados más adelante.

Pérez (2010) plantea que una decisión es una elección consciente y racional, orientada a conseguir un objetivo, que se realiza entre diversas posibilidades de actuación (o alternativas). Antes de tomar una decisión se debe calcular cual será el resultado de escoger una alternativa. En función de las consecuencias previsibles para cada alternativa se tomará la decisión.

Fernández () opina que una decisión es simplemente una elección entre dos o más líneas de acción diferentes. Existen elecciones que tienen poca importancia y se realizan de forma casi automática; sin embargo, otras son de gran transcendencia para la persona o para la empresa. La mayoría de estas decisiones pueden valorarse normalmente en términos monetarios, presentan, pues, un aspecto económico, y por tanto la elección dependerá de los criterios económicos – matemáticos que existen.

Como tomar una decisión supone escoger la mejor alternativa de entre las posibles, se necesita información sobre cada una de estas alternativas y sus consecuencias respecto a nuestro objetivo. La importancia de la información en la toma de decisiones queda patente en la definición de decisión propuesta por Forrester, entendiendo por esta «el proceso de transformación de la información en acción». La información es la materia prima, el input de la decisión, y una vez tratada adecuadamente dentro del proceso de la toma de decisión se obtiene como output la acción a ejecutar. La realización de la acción elegida genera nueva información que se integrará a la información existente para servir de base a una nueva decisión origen de una nueva acción y así sucesivamente. Todo ello debido a una de las características de los sistemas cibernéticos que es la retroalimentación o Feedback. Desde autores de años anteriores se maneja este criterio evidenciándose en el gráfico que se muestra en el Anexo 1.

Resumiendo una decisión es la selección de la alternativa, sobre la base del análisis científico, que mejor responda a los objetivos empresariales.

Teoría de la Decisión.

En cualquier empresa se adoptan diariamente múltiples decisiones que inciden en el éxito de su actividad y en los resultados. La teoría de la decisión explica los distintos factores que intervienen en la toma de decisiones y ayuda en la elección de las opciones más adecuadas para cada caso concreto.

La Teoría de la Decisión, se enfoca en los textos desde dos puntos de vista: como proceso y como técnica cuantitativa.

Delgado (2008) define la toma de decisiones como un proceso ya que permite hacer una elección entre las alternativas o formas para resolver diferentes situaciones de la vida, las que se pueden presentar en diferentes contextos: a nivel laboral familiar sentimental, es decir, en todo momento se toman decisiones, la diferencia entre cada una de estas es el proceso o la forma en la cual se llega a ellas. Consiste, básicamente, en elegir una alternativa entre las disponibles, a los efectos de resolver un problema actual o potencial, (aún cuando no se evidencie un conflicto latente).

Como técnica cuantitativa López y Martínez (2005) plantean que la Teoría de la Decisión constituye una técnica matemática que permite determinar la mejor alternativa o curso de acción a fin de resolver un determinado problema económico, fundamentalmente en situaciones para las cuales la información es insegura o en algunos casos casi inexistentes.

La Teoría de la Decisión, en su sentido más amplio, tiene como objeto de estudio la toma racional de decisiones, recomendando que en vez de individual sea realizada en forma grupal o colectiva, por las ventajas que representa.

Al decir de ciertos autores, la Teoría de la Decisión tiene un carácter de ciencia empírica y normativa, por cuanto sus conclusiones se hallan permanentemente sometidas al contraste de la experiencia y sus planteamientos se refieren también, permanentemente «a lo que debe ser» en una acepción claramente prescriptiva.

El aspecto esencial de los problemas que aborda la Teoría de la Decisión es que, para su solución, debe solo escogerse una alternativa o curso de acción dentro de las posibles, y la selección de dicha acción debe hacerse antes de que se conozca que evento (acciones externas no sujetas al control del decisor) ocurrirá.

En general esta teoría provee de herramientas para la toma de decisiones empresariales, ya que cuando el riesgo puede ser medido esta te provee de mecanismos para analizar la decisión en función de los riesgos mediante los diferentes modelos de criterios.

Modelos de criterios para tomar decisiones.

Teniendo en cuenta que los modelos son herramientas dentro de los Métodos cuantitativos podemos resumir que: un modelo de decisión debe considerarse como un vehículo para resumir un problema de decisión de forma tal que haga posible la identificación y evaluación sistemática de todas las alternativas de decisión del problema. Después se llega a una decisión seleccionando la alternativa que se juzgue sea la mejor entre todas las opciones disponibles.

A su vez la teoría de decisiones proporciona una manera útil de clasificar estos modelos para la toma de decisiones. Supongamos que se ha definido el problema, que se tienen todos los datos y que se han identificado los cursos de acción alternativos. La tarea es entonces seleccionar la mejor alternativa. La teoría de decisiones dice que esta tarea de hacer una selección caerá en una de las cuatro categorías generales dependiendo de la habilidad personal para predecir las consecuencias de cada alternativa.

Categorías	Consecuencias	Criterios de decisión asociados
Certidumbre o certeza	Deterministas	Álgebra. Análisis de punto de equilibrio. Beneficio/Costo. Cálculo matemático. Programación matemática: lineal, no lineal, entera, dinámica y metas. Programación de la producción. Control de inventarios.
Riesgo	Probabilistas	Criterio del Valor Esperado. Criterio de la Pérdida de Oportunidad Esperada. Análisis Estadístico Cálculo y pruebas de Hipótesis. Estadística Bayesiana. Correlación y Regresión. Análisis de Varianza. Métodos no paramétricos. Teoría de colas. Simulación. Métodos Heurísticos. Técnica de Análisis en Redes. Árboles de Decisión. PERT Y CPM. Teoría de Utilidad.
Incertidumbre	Desconocidas	Criterio Pesimista o de Wald. Criterio Optimista. Criterio de Laplace. Criterio de Savage. Criterio de Hurwicz.
Conflicto	Influidas por el oponente	Juegos. Teorías de juegos.

Tabla 1: Modelos de criterios para la toma de decisiones.

Fuente: Elaboración propia.

La Teoría de la Decisión proporciona una manera útil de clasificar los tipos de situaciones en que puede tomar una decisión, en función del «ambiente» de la decisión, esto es, según sea el conocimiento que se tenga sobre el conjunto de los estados de la naturaleza.

Ambiente de Certeza o certidumbre: se presenta cuando el decisor conoce con precisión, y a priori, el estado de la naturaleza que va a presentarse y cuáles son los efectos de las acciones. Existe una relación directa de causa y efecto en cada efecto y su consecuencia, por tanto hay un solo resultado para cada decisión. Simplemente se evalúan las consecuencias de cada acción alternativa y se selecciona la que se prefiere. En la práctica, resulta más difícil.
Ambiente de riesgo: se presenta cuando el conjunto de los estados de la naturaleza es de carácter aleatorio, conociéndose la probabilidad de ocurrencia de cada uno de ellos. Cuando más complejos son los problemas y cuanto más aumenta el número de alternativas posibles, así como el número e importancia de los factores que se están considerando, tanto mayor es el coeficiente de riesgo en la adopción de decisiones. La habilidad del que toma la decisión está precisamente en saber valorar donde es posible reducir al mínimo el coeficiente de riesgo. Una vía para valorar el riesgo es la introducción de probabilidades.

Las fuentes de las probabilidades pueden ser:

La historia del pasado: Si se puede suponer que el futuro será parecido al pasado, las frecuencias relativas se convierten en las probabilidades de los eventos futuros.
El juicio subjetivo: a probabilidad subjetiva es aquella que le asigna una persona a un evento o estado de la naturaleza basándose en su juicio subjetivo.

Ambiente de incertidumbre: se presenta cuando el conjunto de los estados de la naturaleza es aleatorio, pero no se conoce o no puede establecerse la probabilidad de ocurrencia de cada uno de ellos, es decir, que existe incertidumbre cuando el problema económico a resolver no se ha presentado con anterioridad, y entonces debemos acudir a criterios cualitativos en vez de cuantitativos. En tales circunstancias, cada decisión alternativa o curso de acción conducirá a un resultado posible, contenido dentro de un conjunto de resultados posibles, pero no se puede saber que resultado se obtendrá, ni tampoco aplicar criterios deterministas.

En este caso se corre un riesgo mayor de tomar una decisión totalmente desacertada. El que toma la decisión puede en este caso tener una actitud optimista, o pesimista o adoptar una actitud intermedia, ya que puede reflejar los valores personales y las actitudes fundamentales hacia el riesgo que acepta correr.

Toma de decisión bajo Conflicto: esta es la última de las 4 categorías. Aquí se tienen aquellos casos de toma de decisiones bajo incertidumbre en los que hay un oponente. Las probabilidades no solo se desconocen; están influenciadas por un oponente cuya meta es vencer. Esta es la situación crítica de cualquier competencia.

De acuerdo con esto se da lugar a una manera de clasificar los modelos para la toma de decisiones.

Igualmente otros autores definen los modelos de criterios de decisión manteniendo los dos primeros y dividiendo el estado de la naturaleza de incertidumbre:

Certeza: Sabemos con seguridad cuáles son los efectos de las acciones.
Riesgo: No sabemos qué ocurrirá tomando determinadas decisiones, pero sí sabemos qué puede ocurrir y cuál es la probabilidad de ello.
Incertidumbre estructurada: No sabemos qué ocurrirá tomando determinadas decisiones, pero sí sabemos qué puede ocurrir de entre varias posibilidades.
Incertidumbre no estructurada: En este caso no sabemos qué puede ocurrir ni tampoco qué probabilidades hay para cada posibilidad. Es cuando no tenemos ni idea qué puede pasar.

La información asociada a los problemas tratados por la teoría de la decisión se representan normalmente mediante herramientas que en un caso se trata de un modelo matricial denominado matriz de decisión o matriz de pagos y en el otro de los llamados árboles de decisión.

En su mayor parte cuando se emplean métodos cuantitativos para la toma de decisiones, el énfasis está en los medios, o en la mejor manera de alcanzar el objetivo estipulado.

2. Funciones administrativas de la Toma de Decisiones.

La toma de decisiones en una organización abarca a las cuatro funciones administrativas, así los administradores cuando planean, organizan, conducen y controlan están tomando decisiones. Estas funciones pueden ser desglosadas según B (2001), como sigue:

Planeación: Selección de misiones así como de las acciones para cumplirlas mediante procedimientos, presupuestos, programas, políticas, estrategias, objetivos y propósitos, dando respuesta a:

¿Cuáles son los objetivos de la organización, a largo plazo?
¿Qué estrategias son mejores para lograr este objetivo?
¿Cuáles deben ser los objetivos a corto plazo?
¿Cuán altas deben ser las metas individuales?
- Organización: Establecimiento de la estructura que desempeñan los individuos dentro de la organización a través de la división del trabajo, descripción de funciones, departamentalización y jerarquización, respondiendo a:
¿Cuánta centralización debe existir en la organización?
¿Cómo deben diseñarse los puestos?
¿Quién está mejor calificado para ocupar un puesto vacante?
¿Cuándo debe una organización instrumentar una estructura diferente?
- Dirección o ejecución: En esta función se requiere que los administradores influyan en los individuos para el cumplimiento de las metas organizacionales y grupales mediante la supervisión, comunicación, motivación e integración, preguntándose:
¿Cómo manejo a un grupo de trabajadores que parecen tener una motivación baja?
¿Cuál es el estilo de liderazgo más eficaz para una situación dada?
¿Cómo afectará un cambio específico a la productividad del trabajador?
¿Cuándo es adecuado estimular el conflicto?
- Control: Es la medición y corrección del desempeño individual y organizacional de manera tal que se puedan lograr los planes apoyándose en la retroalimentación, corrección y medición, para lo cual se pregunta:
¿Qué actividades en la organización necesitan ser controladas?
¿Cómo deben controlarse estas actividades?
¿Cuándo es significativa una desviación en el desempeño?
¿Cuándo la organización está desempeñándose de manera efectiva?

Como se ha demostrado el análisis de decisiones sustenta todas las funciones directivas. Nada de lo que un directivo hace es más importante que el uso de la mejor información disponible para tomar buenas decisiones.

3. Etapas de la Toma de Decisiones.

Muchos autores definen etapas o pasos para la toma decisiones indistintamente, no obstante de acuerdo a la revisión bibliográfica efectuada se decidió mencionar en este acápite aquellos que tratan el proceso dentro de las etapas y más adelante se valoran los pasos, existiendo semejanzas entre ambas definiciones.

Fernández () define que la toma de decisiones es un proceso racional y sistemático, y su ordenación constituye una secuencia de etapas bien definidas cada una de las cuales es a su vez racional y sistemática, aunque en las decisiones comente que tales etapas se confundan entre sí, según él Jobn Dewey enumera tres etapas:

¿Cuál es el problema?
¿Cuáles son las alternativas?
¿Que alternativa es la mejor?

Se presupone, pues, la existencia de un problema, considerándolo en sentido racional como los obstáculos que se interponen en el logro de los objetivos. La determinación de los objetivos define, por tanto, los diversos tipos de problemas que pueden surgir. Dadas las dificultades que existen en la mayoría de las veces de establecer una definición exacta del problema, se suele realizar en la práctica una formulación inicial para después mediante progresivas aproximaciones llegar a la identificación del mismo. La razón de ello está en reducir tiempo y coste en la investigación.

Por otra parte, un problema no existe si el que va a tomar una decisión no puede elegir entre dos o más cursos de acción posibles. Sin embargo, para llegar a una solución se tiene que conocer qué alternativa es la mejor para conseguir los objetivos fijados, basándose fundamentalmente en la utilización óptima de los recursos.

Según los autores A., S. y W. (2006) en el siguiente diagrama se muestra una clasificación alterna del proceso de toma de decisiones en etapas o fases.

Gráfico 1: Etapas de la toma de decisiones.

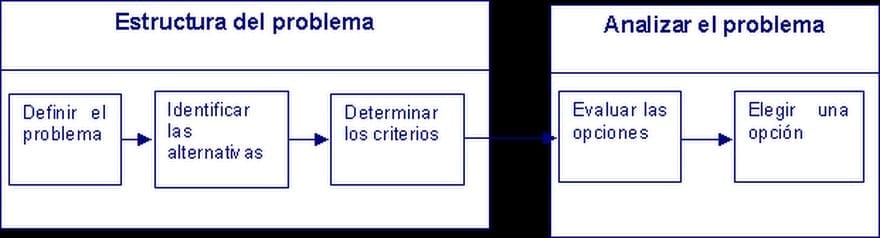
Modelos Toma de Decisiones. Fuente: A., S. y W. (2006) Análisis Cuantitativo y el Proceso de Toma de Decisiones

En este se han combinado las tres primeras fases del proceso decisorio bajo el encabezamiento de «Estructuración del problema» y las dos últimas fases bajo el encabezado «Análisis del Problema».

Es importante señalar que la fase de análisis del proceso de toma de decisiones puede asumir dos formas básicas: cuantitativa y cualitativa. Al mismo tiempo que los directivos tienen aptitudes para el método cualitativo, las cuales, además, usualmente aumentan con la experiencia, las facultades para el método cuantitativo sólo pueden aprenderse estudiando los supuestos y los métodos de la ciencia de la administración. Un administrador puede incrementar su efectividad en la toma de decisiones aprendiendo más sobre la terminología cuantitativa y comprendiendo mejor cuál es su contribución al proceso de toma de decisiones. El administrador que conoce los procedimientos de la toma de decisiones cuantitativas está en una mejor posición para comparar y evaluar las fuentes de recomendaciones tanto cualitativas como cuantitativas para, finalmente, combinar las dos fuentes y tomar la mejor decisión posible.

La etapa de la definición del problema es el componente crucial para determinar el éxito o el fracaso de cualquier enfoque cuantitativo a la toma de decisiones. Normalmente requiere de imaginación, trabajo en equipo y un esfuerzo considerable para convertir una descripción un tanto general de un problema en un problema bien definido que pueda ser abordado cuantitativamente.

Para tener éxito al aplicar el método cuantitativo en la toma de decisiones, el científico de administración debe trabajar en forma estrecha con el gerente o administrador, o con el usuario de los resultados. Cuando los decisores están de acuerdo en que el problema ha quedado definido en forma adecuada, el científico de administración comienza su labor de desarrollar un modelo que se pueda utilizar para representar el problema en términos matemáticos. Después se pueden desarrollar procedimientos de solución para el modelo con objeto de elegir la decisión que resuelva el problema de la «mejor manera».

Por otro lado B, (2001), define que las etapas de la Toma De Decisión son las siguientes:

Identificación y diagnóstico del problema: se reconoce en la fase inicial el problema que deseamos solucionar, teniendo en cuenta el estado actual con respecto al estado deseado. Una vez que el problema es identificado se debe realizar el diagnóstico y luego de esto podremos desarrollar las medidas correctivas.
Generación de soluciones alternativas: La solución de los problemas puede lograrse por varios caminos y no sólo seleccionar entre dos alternativas, se pueden formular hipótesis ya que con la alternativa hay incertidumbres.
Selección de la mejor alternativa: Esta tercera etapa implica la determinación del valor o la adecuación de las alternativas que se generaron. ¿Cuál solución será la mejor?
Evaluación de alternativas: Los gerentes deben considerar distintos tipos de consecuencias y a su vez intentar predecir los efectos sobre las medidas financieras u otras medidas de desarrollo, existiendo también otras consecuencias menos definidas que hay que atender. Las decisiones establecen un precedente y hay que determinar si este será una ayuda o un obstáculo en el futuro. Por supuesto, no es posible predecir los resultados con toda precisión. Entonces pueden generar planes de contingencia, esto es, curso alternativo de acción que se pueden implantar con base en el desarrollo de los acontecimientos.
Evaluación de la decisión: Cuando el administrador ha considerado las posibles consecuencias de sus opciones, ya está en condiciones de tomar la decisión. Debe considerar tres términos muy importantes. Estos son: maximizar (tomar la mejor decisión posible), satisfacer (elección de la primera opción que sea mínimamente aceptable o adecuada, satisfaciendo una meta o criterio buscado) y optimizar (el mejor equilibrio posible entre distintas metas).
Implantación de la decisión: El proceso no finaliza cuando la decisión se toma; esta debe ser implementada. Bien puede ser que quienes participen en la elección de una decisión sean quienes procedan a implementarla, como en otras ocasiones delegan dicha responsabilidad en otras personas. Debe existir la comprensión total sobre la elección de la toma de decisión en sí, las razones que la motivan y sobre todo debe existir el compromiso de su implementación exitosa. Para tal fin, las personas que participan en esta fase del proceso, deberían estar involucradas desde las primeras etapas que anteriormente hemos mencionado. «Evaluar la decisión», forma parte de la etapa final de este proceso. Se recopila toda la información que nos indique la forma como funciona una decisión, es decir, es un proceso de retroalimentación que podría ser positiva o negativa. Si la retroalimentación es positiva, pues entonces nos indica que podemos continuar sin problemas y que incluso se podría aplicar la misma decisión a otras áreas de la organización. Si por el contrario, la retroalimentación es negativa, podría ser que: 1) tal vez la implementación requiera de más tiempo, recursos, esfuerzos o pensamiento o 2) nos puede indicar que la decisión fue equivocada, para lo cual debemos volver al principio del proceso (re)definición del problema. Si esto ocurriera, sin duda tendríamos más información y probablemente sugerencias que nos ayudarían a evitar los errores cometidos en el primer intento.

A continuación citaremos los pasos que los decisores deben considerar durante la planeación de su ejecución:

Determinar cómo se verán las cosas una vez que la decisión esté funcionando completamente.
Orden cronológico (de ser posible con un diagrama de flujo) de los pasos para lograr una decisión totalmente operativa.
Considerar recursos disponibles y actividades necesarias para poner cada paso en práctica.
Considerar el tiempo que tomará cada una de las etapas.
Asignación de responsabilidades a personas específicas para cada etapa.

Podemos estar seguros de que cuando una toma de decisión es tomada, ésta probablemente generará ciertos problemas durante su ejecución, por lo tanto los gerente deben dedicar el tiempo suficiente al reconocimiento de los inconvenientes que se pueden presentar así como también ver la oportunidad potencial que estos pueden representar.

4. Componentes de la decisión.

Se plantea que los elementos que constituyen la estructura de la decisión son: los objetivos de quién decide y las restricciones para conseguirlos; las alternativas posibles y potenciales; las consecuencias de cada alternativa; el escenario en el que se toma la decisión y las preferencias de quien decide.

B, (2001) plantea que la técnica de tomar decisiones en un problema está basada en cinco componentes primordiales:

Información: Estas se recogen tanto para los aspectos que están a favor como en contra del problema, con el fin de definir sus limitaciones.
Conocimientos: Si quien toma la decisión tiene conocimientos, ya sea de las circunstancias que rodean el problema o de una situación similar, entonces estos pueden utilizarse para seleccionar un curso de acción favorable.
Experiencia: Cuando un individuo soluciona un problema en forma particular, ya sea con resultados buenos o malos, esta experiencia le proporciona información para la solución del próximo problema similar.
Análisis: No puede hablarse de un método en particular para analizar un problema, debe existir un complemento, pero no un reemplazo de los otros ingredientes. En ausencia de un método para analizar matemáticamente un problema es posible estudiarlo con otros métodos diferentes. Si estos otros métodos también fallan, entonces debe confiarse en la intuición.
Juicio: El juicio es necesario para combinar la información, los conocimientos, la experiencia y el análisis, con el fin de seleccionar el curso de acción apropiado. No existen substitutos para el buen juicio.

La mayoría de los autores que tratan la Teoría de la Decisión concuerdan que además de los componentes mencionados anteriormente existen estos cinco elementos básicos que están presentes en una situación de decisión:

La existencia de un conjunto de decisiones alternativas (acciones, cursos de acción, estrategias).
Un conjunto de acciones externas que enfrenta el que toma la decisión, que se denominan estados de la naturaleza, y que constituyen el ambiente o contexto estructural en el que se presenta el problema.
Los resultados que se obtienen por el uso de una alternativa determinada para los posibles estados de la naturaleza.
La existencia de uno o varios decisores a quienes corresponde proponer los criterios de selección y aplicarlos.
El grado de conocimiento que se tiene sobre el comportamiento de los estados de la naturaleza.

De estos elementos, los tres primeros constituyen los elementos intrínsecos o esenciales de una decisión, mientras los dos restantes tienen más bien un carácter metodológico, destacando lo siguiente:

DECISIONES ALTERNATIVAS: Son las alternativas, cursos de acción o estrategias de entre las cuales el que toma la decisión debe elegir. Deben expresarse en términos mutuamente excluyentes.
ESTADOS DE LA NATURALEZA: Son las circunstancias o acciones externas que afectan el resultado de una decisión, pero que están fuera del control del decisor. Se les denomina también EVENTOS y deben expresarse en términos mutuamente excluyentes y ser colectivamente exhaustivos.
RESULTADOS: Pueden expresarse en términos económicos (ganancia, costo, etc.) o en términos de alguna medida no monetaria como preferencias o escalas de valoración.
AMBIENTE de la decisión: Este ambiente puede concretarse, convencionalmente en tres modalidades fundamentales: certeza, riesgo e incertidumbre, aunque algunos autores incluyen como una cuarta: el conflicto.

5. Características de la decisión.

La decisión que se elige se denomina decisión óptima y de acuerdo al criterio de Fernández () se caracterizan por:

Ser una decisión del conjunto de decisiones posibles:

La idea básica es que se trata de la mejor decisión posible. Sin embargo podrían existir más de una si todas ellas son para él igualmente buenas una vez que las ha cuantificado; pero no puede decir que es la mejor si existieran otras decisiones que por desconocimiento no ha considerado en su proceso de toma de decisiones.

Depender del principio de decisión que se utilice:

Un principio de decisión es una regla para especificar cuál de entre todas las decisiones posibles es la óptima. Existen diversos principios que pueden conducir a la existencia de más de una decisión óptima. Por tanto, se puede decir que ésta depende del principio de decisión que emplee el decisor.

Puede ser distinta para personas diferentes en una misma situación de decisión:

En general una decisión puede llevar a una o más consecuencias. Las posibilidades de estas contingencias pueden la mayoría de las veces ser establecidas en términos de probabilidad.

Depender de la información relevante y útil que posea el decisor:

Se considera por algunos autores cómo no racional el ignorar la información relevante para tomar una decisión, aunque existen situaciones concretas en que la implicación de tal información no está muy clara. En la práctica la utilidad de la información es una cuestión de grado. La Teoría de la Decisión permite determinar cuánto tiempo, esfuerzo y dinero es necesario gasta para obtener aquella información.

B (2001) plantea que existen cinco características de las decisiones:

Efectos futuros: Tiene que ver con la medida en que los compromisos relacionados con la decisión afectará el futuro. Una decisión que tiene una influencia a largo plazo, puede ser considerada una decisión de alto nivel, mientras que una decisión con efectos a corto plazo puede ser tomada a un nivel muy inferior.
Reversibilidad: Se refiere a la velocidad con que una decisión puede revertirse y la dificultad que implica hacer este cambio. Si revertir es difícil, se recomienda tomar la decisión a un nivel alto; pero si revertir es fácil, se requiere tomar la decisión a un nivel bajo.
Impacto: Esta característica se refiere a la medida en que otras áreas o actividades se ven afectadas. Si el impacto es extensivo, es indicado tomar la decisión a un nivel alto; un impacto único se asocia con una decisión tomada a un nivel bajo.
Calidad: Este factor se refiere a las relaciones laborales, valores éticos, consideraciones legales, principios básicos de conducta, imagen de la compañía, etc. Si muchos de estos factores están involucrados, se requiere tomar la decisión a un nivel alto; si solo algunos factores son relevantes, se recomienda tomar la decisión a un nivel bajo.
Periodicidad: Este elemento responde a la pregunta de si una decisión se toma frecuente o excepcionalmente. Una decisión excepcional es una decisión de alto nivel, mientras que una decisión que se toma frecuentemente es una decisión de nivel bajo.

6. Pasos en el Proceso de la Toma de Decisiones.

A la hora de establecer los pasos dentro del proceso de toma de decisiones igualmente existe diversidad de criterios por varios autores y en ocasiones coinciden con las etapas como se ha mencionado en acápites anteriores.

Fernández () en su investigación distingue fundamentalmente cinco pasos en todo proceso de decisión, los cuales encierran una metodología científica en la toma de decisiones

Observación de la realidad:

En este primer paso se define el problema en relación con los objetivos propuestos y que están implicados en el mismo, y se identifican por abstracción los factores que influyen en los objetivos.

Representación en un modelo:

Una vez identificados los factores, se seleccionan los que son más relevantes, no teniendo en cuenta aquellos cuya influencia sea mínima. En esta fase se formulan las alternativas y los demás factores del ambiente estructural.

Prueba y verificación del modelo:

El modelo explica de una manera útil aunque no del todo exacta lo que está implicado en el problema en relación con los objetivos propuestos. Sin embargo, no debe tomarse una decisión hasta que el modelo no haya sido probado mediante una contrastación adecuada En general, la verificación dependerá del tipo de contraste elegido y del modelo elaborado.

Desarrollo de una regla de decisión:

Una vez realizada la verificación con resultados satisfactorios, entonces el modelo puede ser utilizado en la toma de decisiones. Sin embargo, es preciso tener en cuenta que es el mejor mientras el sistema para el cual ha sido elaborado no se modifique. Por lo tanto, es necesario crear un mecanismo de control que actúe sobre los resultados y los factores considerados con el fin de realizar los ajustes correspondientes. En definitiva, el modelo se convierte en una regla de decisión que lo relaciona más directamente con los objetivos.

Aplicación:

Finalmente, se pone en práctica la solución obtenida a partir del modelo. Este paso da, pues, por terminado el proceso de decisión.

A su vez B (2001) define 6 pasos en el proceso de la toma de decisiones:

Determinar la necesidad de una decisión:

El proceso de toma de decisiones comienza con el reconocimiento de la necesidad de tomar una decisión, el mismo lo genera un problema o una disparidad entre cierto estado deseado y la condición real del momento.

Identificar los criterios de decisión:

Luego se deben identificar los criterios que sean importantes para la efectuar la decisión.

Asignar peso a los criterios:

Los criterios enumerados en el paso previo no tienen mayor importancia. Es necesario ponderar cada uno de ellos y priorizar su importancia en la decisión.

Desarrollar todas las alternativas:

Es la base de la toma de decisiones y no es más que desplegar las alternativas. El tomador de la decisión tiene que confeccionar una lista de todas las alternativas posibles y que podrían utilizarse para resolver el problema.

Evaluar las alternativas:

Una vez identificadas las alternativas, el tomador de las decisiones tiene que evaluar de manera crítica cada una de ellas. Las ventajas y desventajas de cada alternativa resultan evidentes cuando son comparadas. La evaluación de cada alternativa se efectúa analizándola con respecto al criterio ponderado.

Seleccionar la mejor alternativa (Toma de decisiones):

Una vez seleccionada la mejor alternativa se llega al final del proceso de la toma de decisiones, en el proceso racional. Esta selección es bastante simple. El tomador de decisiones solo tiene que escoger la alternativa que tuvo la calificación más alta en el paso número cinco.

El tomador de decisiones debe ser totalmente objetivo y lógico a la hora de tomarlas, tiene que tener una meta clara y todas las acciones en el proceso de toma de decisiones llevan de manera consistente a la selección de aquellas alternativas que maximizarán la meta.

Por otro lado Robbins (1994) muestra el proceso de toma de decisiones como una serie de ocho pasos (Anexo 2) pudiendo aplicarlo tanto a sus decisiones personales como a una acción de una empresa, a su vez también se puede aplicar tanto a decisiones individuales como grupales.

Paso 1: La identificación de un problema.

El proceso de toma de decisiones comienza con un problema, es decir, la discrepancia entre un estado actual de cosas y un estado que se desea. Ahora bien, antes que se pueda caracterizar alguna cosa como un problema los decisores tienen que ser conscientes de las discrepancias, estar bajo presión para que se tomen acciones y tener los recursos necesarios. Se puede percibir que existe una discrepancia por comparación entre el estado actual de cosas y alguna norma, la cual puede ser el desempeño pasado, metas fijadas con anterioridad o el desempeño de alguna otra unidad dentro de la organización o en otras organizaciones. Además, debe existir algún tipo de presión en esta discrepancia ya que si no el problema se puede posponer hasta algún tiempo en el futuro. Así, para iniciar el proceso de decisión, el problema debe ejercer algún tipo de presión sobre el decisor para que éste actúe. Esta presión puede incluir políticas de la organización, fechas límites, crisis financieras, una próxima evaluación del desempeño etc.

Por último, es poco factible que los administradores califiquen a alguna cosa de problema sino tienen la autoridad, dinero, información, u otros recursos necesarios para poder actuar, ya que sino describen la situación como una en la que se les coloca ante expectativas no realistas.

Paso 2.- La identificación de los criterios para la toma de decisiones.

Una vez que se conoce la existencia del problema, se deben identificar los criterios de decisión que serán relevantes para la resolución del problema. Cada persona que toma decisiones suele tener unos criterios que los guían en su decisión. Este paso nos indica que son tan importantes los criterios que se identifican como los que no; ya que un criterio que no se identifica se considerará irrelevante por el tomador de decisiones. Deberá reunirse información pasada, hechos pertinentes y soluciones previas a problemas semejantes.

Paso 3.- La asignación de ponderaciones a los criterios.

Los criterios seleccionados en la fase anterior no tienen todos la misma importancia, por tanto, es necesario ponderar las variables que se incluyen en las lista en el paso anterior, a fin de darles la prioridad correcta en la decisión. Este paso lo puede llevar a cabo dándole el mayor valor al criterio preferente y luego comparar los demás para valorarlos en relación al preferente.

Paso 4.- El desarrollo de alternativas.

Este paso consiste en la obtención de todas las alternativas viables que puedan tener éxito para la resolución del problema, es decir, se buscan las soluciones posibles y se enumeran.

Paso 5.- Análisis de las alternativas.

Una vez que se han desarrollado las alternativas el tomador de decisiones debe analizarlas cuidadosamente. Las fortalezas y debilidades se vuelven evidentes según se les compare con los criterios y valores establecidos en los pasos 2 y 3. Se evalúa cada alternativa comparándola con los criterios. Algunas valoraciones pueden lograrse en una forma relativamente objetiva, pero, sin embargo, suele existir algo de subjetividad, por lo que la mayoría de las decisiones suelen contener juicios.

Paso 6.- Selección de una alternativa.

Este paso consiste en seleccionar la mejor alternativa de todas las valoradas, por lo que se toma la decisión de cuál de las alternativas cumple mejor con los criterios de solución.

Paso 7.- La implantación de la alternativa.

Mientras que el proceso de selección queda completado con el paso anterior, sin embargo, la decisión puede fallar si no se lleva a cabo correctamente. Este paso intenta que la decisión se lleve a cabo, e incluye dar a conocer la decisión a las personas afectadas y lograr que se comprometan con la misma. Si las personas que tienen que ejecutar una decisión participan en el proceso, es más fácil que apoyen con entusiasmo la misma. Estas decisiones se llevan a cabo por medio de una planificación, organización y dirección efectivas.

Paso 8.- La evaluación de la efectividad de la decisión.

Este último paso juzga en el proceso el resultado de la toma de decisiones para ver si se ha corregido el problema. Si como resultado de esta evaluación se encuentra que todavía existe el problema tendrá que hacer el estudio de lo que se hizo mal. Las respuestas a estas preguntas nos pueden llevar de regreso a uno de los primeros pasos e inclusive al primer paso.

A pesar de existir diferentes criterios de varios autores, la esencia es la misma para seguir los pasos en la toma de decisiones, por lo que este último criterio consideramos es el más completo a pesar de tener una mayor cantidad de pasos que complejizaría el proceso.

7. Tipos de decisiones por su clasificación.

La tipología de la decisión igual que los aspectos tratados anteriormente es de lo más polifacético.

B (2001) plantea que las decisiones, pueden estar divididas en dos categorías.

Decisión Programada:

Son programadas en la medida que son repetitivas y rutinarias, así mismo en la medida que se ha desarrollado un método definitivo para poder manejarlas. Al estar el problema bien estructurado, el mando no tiene necesidad de pasar por el trabajo y gasto de realizar un proceso completo de decisión.

Estas decisiones programadas cuentan con unas guías o procedimientos (pasos secuenciales para resolver un problema) unas reglas que garanticen consistencias en las disciplinas y con un alto nivel de justicia, aparte de una política, que son las directrices para canalizar el pensamiento del mando en una dirección concreta.

Decisión no Programada:

«La reestructuración de una organización» o «cerrar una división no rentable”, son ejemplos de decisiones no programadas, También «la creación de una estrategia de mercado para un nuevo producto».

A., S. y W. (2006) en su artículo Análisis Cuantitativo y el Proceso de Toma de Decisiones definen de manera general los diferentes tipos de decisiones que pueden existir de acuerdo a su clasificación, considerándose como la más completa, mostrándose a continuación.

No.	Clasificación	Tipo de Decisión
1.	Según el sujeto que decide, tenemos:	· Decisiones individuales: tomadas por una sola persona. · Decisiones grupales: tomadas por un grupo de personas a través de una discusión.
2.	Según el contenido de la decisión y el enfoque básico del que decide (método utilizado):	· Decisiones programables o programadas: Son las que resuelven asuntos repetidos y que pueden ser de rutina. · Decisiones no programables: Las que afrontan situaciones que en lo esencial son nuevas e inéditas. Para su resolución se utiliza la intuición, creatividad o criterio personal del decisor.
3.	Según las repercusiones que originan:	· Decisiones sobre uno mismo: Yo decido hospedarme en un hotel de lujo o en uno de segunda. · Decisiones sobre otros: Un padre decide que su hijo entre al Tecnológico de Monterrey en vez de inscribirlo en la Universidad Anáhuac.
4.	Según el conocimiento de los datos y las circunstancias:	· Decisiones en situación de certidumbre: Cuando cada curso de acción lleva a un resultado ya conocido de antemano por el que decide. Ejemplo: Elegir una bebida y escoger entre varias que son familiares: cerveza, coca-cola, agua de limón. · Decisiones en situación de incertidumbre: Cuando cada curso de acción, o uno de ellos, me llevarán por caminos desconocidos para mí. Ejemplo: contratación de una persona.
5.	Según el tipo de autoridad que las fundamenta, hay:	· Decisiones técnicas: Cuando se apoyan en la competencia de un experto. Ejemplo: el mecánico decide cambiarle la bomba de gasolina al coche. · Decisiones ejecutivas: Cuando nacen de un poder social, más que de la competencia de un experto. Ejemplo: Por decisión del director general dos personas participan en un congreso internacional.
6.	Según el nivel jerárquico:	· Decisiones operativas: Las que competen a los obreros y supervisores. · Decisiones tácticas: Se manejan en el nivel de Jefe de Departamento y directores de Sección. · Decisiones estratégicas: Competen a la dirección general: fijan los objetivos y políticas generales de las instituciones.
7.	Según la participación de los interesados:	· Decisiones autoritarias: Las que son impuestas por un jefe más o menos dictatorial. · Decisiones por votación: Cuando al no poder llegar a un acuerdo entre los interesados, se toma el parecer y el deseo de la mayoría; la minoría supuestamente se resigna y acepta. · Decisiones por unanimidad: Cuando de entrada, o como fruto de un intercambio de puntos de vista, todos coinciden en un mismo parecer.
8.	Según su eficacia:	· Decisiones buenas: Cuando se producen los resultados deseados y previstos. · Decisiones malas: En el caso contrario.
9.	Clasificación sintética:	· Decisiones estructuradas: = Decisiones programadas. Se usan métodos matemáticos y reglas de decisión. · Decisiones semiestructuradas: En este tipo de decisiones sólo parte del problema tiene una respuesta ya definida proporcionada por un procedimiento que es aceptado. · Decisiones no estructuradas: = Decisiones no programadas. No se pueden utilizar métodos matemáticos o reglas de ningún tipo

Tabla 2: Tipos de decisiones por su clasificación.

Fuente: A., S. y W. (2006) Análisis Cuantitativo y el Proceso de Toma de Decisiones

Cuando se trata de decisiones que afectan a otros, hay que considerar dos dimensiones: la calidad objetiva de las decisiones, y la aceptación por parte de quienes han de llevarla a la práctica o se verán afectados por ella; de tal modo que la Bondad (B) viene a ser un producto de la Calidad (C) por la Aceptación (A):

B= C x A.

Siendo este un criterio completo respecto a las tipologías que existen para tomar decisiones.

8. Importancia de la Toma de Decisiones.

Es importante la toma de decisiones porque mediante un buen juicio se indica que problema o situación es valorado y considerado profundamente para elegir el mejor camino a seguir según las diferentes alternativas y operaciones.

En la toma de decisiones, considerar un problema y llegar a una conclusión válida, significa que se han examinado todas las alternativas y que la elección ha sido correcta, lo que le permite a la empresa elevar su nivel de eficiencia y eficacia, utilizando los métodos económicos matemáticos como uno de los enfoques más competitivos de investigación y análisis para la toma de las decisiones. También es de vital importancia para la administración ya que contribuye a mantener la armonía y coherencia del grupo.

Las ventajas de la utilización de los diferentes métodos económicos – matemáticos en la toma de decisiones pueden resumirse como sigue:

Proporciona a quienes toman las decisiones un conjunto de conceptos y herramientas que los capacitan para tomar decisiones de una manera lógica y consistente y con tanta precisión como sea posible, es decir, genera una mejor decisión.
Le da a quienes toman decisiones una visión mejorada del sistema y problema acerca del cual deberán decidir, de tal manera que ellos puedan perfeccionar su propio proceso intuitivo de toma de decisiones.
El enfoque a través de los métodos económicos – matemáticos y la cuantificación del problema facilita la comunicación y coordinación.

El proceso de toma de decisiones es importante, según Busto (2007), porque proporciona un marco de trabajo y una metodología con la cual decidir cuando los resultados son inciertos.

Plantea que independientemente de las ventajas que trae consigo la toma de decisiones se pueden presentar algunas limitaciones, ya que las decisiones pueden no ser muy distintas de la que se logra por medio de la reflexión basada en la experiencia y sin un proceso sistemático.

Las decisiones equivocadas más catastróficos se deben a que nadie se preguntó lo obvio, es decir, no se cuestiona el enunciado, no se definen criterios ni se identifican riesgos.

Barreras para la toma eficaz de decisiones.

Ilusión de control: Creencia de las personas que pueden influir en acontecimientos, incluso cuando no tienen control sobre lo que sucederá.
Efectos de encuadre: Prejuicio psicológico al que afecta la manera en que un problema o decisión alternativa se presenta o plantea.
Desestimar el futuro: Dar mayor peso a los costos y beneficios a corto plazo que a los de largo plazo.
Presiones de tiempo: Los premios son para la acción rápida y para quienes mantienen el paso.

Importancia de la toma de decisiones en grupo.

Si bien el decisor casi siempre toma las decisiones solo, hay ocasiones en que debe aprovechar la ventaja de contar con un grupo de expertos para tomar ciertos caminos.

La toma de decisiones en grupo puede utilizarse con mucha eficiencia si el decisor líder maneja la situación como debe ser. Uno de los factores más importantes consiste en ganarse el apoyo de los miembros del grupo; señalándoles el valor de sus aportes en la solución del problema. Un segundo enfoque muy útil consiste en dar a cada integrante del grupo elementos específicos en que pensar y trabajar, para que pueda reconocer sus aportes; también crear un entorno donde las personas puedan expresarse abierta y francamente y que estimule tanto los aportes creativos como las discusiones sobre las fallas o los errores en que podría incurrirse.

La toma de decisiones en las organizaciones modernas es realizada en grupo o comités de trabajo, teniendo sus ventajas y desventajas, que influyen de manera determinante en el rol de la gerencia de nuestras organizaciones.

Ventajas de la toma de decisiones grupal:

Información y conocimiento más completos: Lógicamente un grupo logra recopilar más información, teniendo acceso a más fuentes informativas que un solo individuo, independiente de la educación y de la experiencia de este. Por lo tanto los grupos pueden ofrecer mayores aportes, tanto en la cantidad como en la diversidad para la Toma de decisiones.
Incrementar la aceptación de una solución o bien la variedad de puntos de vista: Muchas decisiones fracasan después de elegida una opinión, debido a que un sector de gente no la acepta como una solución posible, cada uno de sus integrantes tiene un punto de vista propio que difiere, en cierta medida, del de los demás, como resultado, la cantidad y tipos de opciones son mayores que los del individuo que trabaja solo. La participación en grupo facilita una amplia discusión y una aceptación más participativa, es posible que haya divergencias en los acuerdos, pero se plantea y permite su discusión para cuando ya sea aceptada, sea un compromiso de todo un conjunto. Es difícil que los asistentes al grupo de discusión ataquen o dificulten una decisión que ellos ayudaron a desarrollar. Las decisiones grupales incrementan la aceptación de la solución final y facilitan su instrumentación.
Incrementan la Legitimidad: Los métodos democráticos son aceptados por todos los componentes de la sociedad. Cuando el proceso es grupal, intervienen todos los aditamentos de los ideales democráticos. Si el tomador de decisiones no consulta a otros antes de tomar una de ellas, el hecho del poder que tiene no le exime de quedar como una persona autoritaria y arbitraria. Las decisiones grupales no tienen la varita mágica de la perfección, pero sin lugar a dudas son las menos peligrosas y por lo tanto las que tienen un menor nivel de error.
Reducción de los problemas de comunicación: Puesto que el grupo participa en la toma de decisión, todos sus integrantes están conscientes de la situación, por lo general la puesta en marcha de la solución se realiza sin tropiezos. Las preguntas, las objeciones y los obstáculos a los que normalmente se enfrenta la implantación de una decisión, con frecuencia desaparecen, cuando esta última es resultado de la participación del grupo.

Desventajas de la toma de decisiones grupal:

Requieren mucho tiempo: El reunir al grupo toma su tiempo, pero con una buena organización, las reuniones estarán programadas de antemano en un espacio de tiempo oportuno (varía de acuerdo a la organización y no debe ser menor de dos semanas). El resultado es que los grupos consumen más tiempo en alcanzar una decisión a diferencia de un solo individuo.
Presiones de aceptación: Si bien se supone que todos los miembros del grupo deben sentirse libre para expresar sus opiniones, sugerencias y recomendaciones, no deja de ser cierto que a veces existe cierta presión para que todo el mundo se reúna y acate el consenso general, llamado con frecuencia «Pensamiento grupal». Esta presión puede provocar que el grupo pase por alto un consejo o sugerencia positiva de algunos de los presentes. Se presiona a los inconformes para que se ajusten y adhieran a la opinión de la mayoría.

Finalmente se llegará a un mismo resultado que necesariamente debe ser aceptado por todos para tener validez.

Responsabilidad ambigua: Los miembros de un grupo tienen que compartir la responsabilidad, por lo tanto la individualidad se diluye, dándole un gran valor a los resultados.
El Compromiso: En ciertas ocasiones el grupo se estanca y se muestra incapaz de llegar a un acuerdo sobre qué soluciones recomendar. Obligados a tomar una decisión, se alienta a los miembros a llegar a un compromiso o a darse por vencidos, aceptando una versión diferente de su solución. Este inconveniente es muy usual cuando el grupo se subdivide en grupos más pequeños, cada uno de los cuales apoya una solución diferente.

9. Métodos y Procesos Multicriterios para la Toma de Decisiones. Ejemplos.

Es habitual que el ser humano deba tomar decisiones sobre problemas de cierta complejidad que incluyen varios objetivos, que pueden ser total o parcialmente conflictivos entre sí, de manera que la mejora en cualquiera de ellos puede empeorar el valor de otros, objetivos que son evaluados de acuerdo a múltiples criterios y donde no es evidente “la mejor” u óptima alternativa.

La flexibilidad y adaptabilidad es una de las características que sobresalen en los métodos de decisión Multicriterio, ya que, de hecho, cualquier decisión será el resultado de una combinación o compromiso entre los objetivos contrapuestos a los que se ha de enfrentar un decisor. Así, un modelo que muestre explícitos los diferentes criterios y objetivos puede ser utilizado como un instrumento de búsqueda del consenso, siendo ésta una de las más interesantes facetas del análisis multicriterio.

Vitoriano (2007) define que se trata de establecer las alternativas o puntos factibles existentes, clasificando los conjuntos:

Conjunto discreto: es factible enumerar y tratar explícitamente cada uno de las alternativas posibles.
Conjunto continuo: cuando no se define el conjunto de alternativas se habla de conjunto o región factible, el cual a vez, puede venir definido de forma rígida mediante restricciones o de forma más flexible mediante lo que se conoce como niveles de aspiración.

A continuación se exponen algunos conceptos básicos de la decisión multicriterio:

Atributo: “valor” observado (medido) de una decisión independientemente del decisor. Los atributos suelen ser competidores o contradictorios entre sí.
Objetivo: dirección de mejora de un atributo, la que será de maximización o minimización en el caso de atributos numéricos y en el caso de atributos no numéricos vendrá dado por un sistema de preferencias.
Nivel de aspiración: es un nivel aceptable de logro para un atributo.
Meta: es la combinación de un atributo con su nivel de aspiración.
Criterio: son los atributos, objetivos o metas relevantes en un problema de decisión.
Solución de mejor compromiso: solución del conjunto eficiente que es seleccionada por el decisor.

La teoría de la Decisión Multicriterio constituye un marco general o paradigma decisional en el que subyacen diferentes atributos, objetivos o metas.

Este autor da la siguiente clasificación para los métodos Multicriterios:

Métodos de decisión multicriterio continua:

-Métodos de optimización multiobjetivo.

Métodos para generar el conjunto eficiente en su totalidad.

Método de las ponderaciones (Zadeh, 1963).

Método de las ε-restricciones (Marglin, 1967).

Método simplex multiobjetivo (Zeleny, 1973).

Métodos para dar una solución compromiso (Yu, 1973 y Zeleny, 1973, 1974.

-Métodos satisfacientes o programación por metas (Simon, 1955).

Programación por metas ponderadas.
Programación por metas MINIMAX o Tchebychev.
Programación por metas lexicográficas.

Métodos de decisión multicriterio discretos.

Procesos analíticos jerarquizados (método AHP) (Saaty, 1977).
Método Electre (Benayoun, Roy y Sussman, 1966)

La Programación Multiobjetivo constituye un enfoque multicriterio de gran potencialidad cuando el contexto decisional está definido por una serie de objetivos a optimizar que deben de satisfacer un determinado conjunto de restricciones.

Como la optimización simultánea de todos los objetivos es usualmente imposible, pues en la vida real entre los objetivos que pretende optimizar un centro decisor suele existir un cierto grado de conflicto el enfoque multiobjetivo en vez de intentar determinar un óptimo existente pretende establecer el conjunto de soluciones eficientes o Pareto óptimas.

Un conjunto de soluciones es eficiente (o Pareto Óptima) cuando está formado por soluciones factibles, tal que no existe otra solución factible que proporcione una mejora en uno de los atributos sin producir empeoramiento en al menos otro de los atributos.

En la programación por meta también se tiene una función objetivo que optimizar sujeta a una o más restricciones. Sin embargo, dentro de este marco de referencia se agregarán dos conceptos nuevos. El primero es el de las restricciones de meta en lugar de las restricciones de recurso que se han analizado y el segundo concepto es el de rango de prioridad entre las funciones de objetivo.

Una ventaja importante de la programación meta es su flexibilidad en el sentido de que permite al tomador de decisiones, experimentar con una multitud de variaciones de las restricciones y de prioridades de las metas cuando se involucra con un problema de decisión de objetivos múltiples.

Rodríguez, Bilbao, Arenas, Pérez y Antomil plantean que son muchos los problemas de naturaleza económica que se caracterizan porque en la elección de la mejor decisión se han de tener en cuenta varios criterios y, por tanto, se desea alcanzar más de un objetivo. La programación multiobjetivo y, en general, la teoría de la decisión multicriterio, se encarga de la resolución de problemas de este tipo y, por tanto, existen muchos trabajos en los que se aplica dicha teoría a problemas de naturaleza económica.

Las técnicas de decisión multicriterio, M.C.D.M., se suelen dividir en dos grandes bloques, según las características de los problemas que afronten:

A.D.M. -Técnicas de Decisión Multiatributo, dedicadas al estudio de problemas en los que las relaciones atributos-objetivos son sencillas y permiten identificar ambos conceptos y donde el conjunto de posibles decisiones es discreto; son técnicas asociadas a la idea de selección entre alternativas predeterminadas.
O.D.M – Técnicas de Decisión Multiobjetivo o bien de Optimización Multiobjetivo, asociadas a la idea de búsqueda de alternativas eficientes, donde el conjunto de decisiones se considera continuo y donde los objetivos vienen descritos en términos de funciones.

La información disponible para modelizar y posteriormente resolver un problema es relevante para la clasificación de las técnicas multicriterio. Según sea tal flujo podemos distinguir entre métodos sin información y métodos con información.

Métodos sin información: se basan únicamente en la estructura matemática del problema, sin tener ningún conocimiento previo de las preferencias del decisor y se abordan a través de las «técnicas generadoras» que dan como solución del modelo un conjunto de puntos eficientes:

Métodos Escalarizantes: tienen en común la idea de convertir todas las funciones objetivo en una sola; proporcionan información sobre las tasas de intercambio entre los distintos objetivos y sirven como punto de partida para otras técnicas.

Método de las Ponderaciones.
Método de la Restricción.
Programación Compromiso: se basa en el concepto de punto ideal y trata de encontrar la combinación de valores para las funciones objetivo factibles más cercanas al mismo.

Métodos con información: el decisor manifiesta sus preferencias. Si esta información es disponible antes de la formulación de los modelos, puede ser recogida en los niveles de aspiración y en el establecimiento de prioridades entre objetivos. No sólo se trata de formular y resolver el problema planteado, sino de intentar que las soluciones que se obtengan se ajusten a las preferencias expresadas por el decisor.

Programación por Metas: se determinan soluciones que resulten satisfactorias para el decisor.
Métodos interactivos: el intercambio de información se realiza de manera continuada a lo largo de la resolución del problema.

Delgado (2008) plantea que actualmente existen numerosos instrumentos matemáticos adecuados para servir de ayuda a la toma de decisiones con criterios múltiples, donde el término atributo hace referencia a las características que describen cada una de las alternativas disponibles en una situación de decisión, refiriéndose a valores relacionados con una realidad objetiva.

Por su parte los criterios constituyen atributos, objetivo o metas que se consideran relevantes para un cierto problema decisional. Desde un punto de vista general, Zeleny (1982) define los criterios como medidas, reglas y estándares que guían la decisión. Por consiguiente la teoría de la decisión multicriterio constituye un marco general o paradigma decisional en el que subyacen diferentes atributos, objetivos o metas.

Diversos autores se han ocupado de describir, de modo generalizado, un proceso de decisión con criterios múltiples, destacando las distintas partes y fases del mismo. Entre dichos autores se mencionan a Zeleny (1982), Chankong y Haimes (1983) y Goicochea, Hansen y Duckstein (1982), los cuales han constituido fuente de referencia obligada en la elaboración del algoritmo de los pasos del proceso de decisión con criterios múltiples clasificándose de acuerdo a como se muestra en el Anexo 3.

Los métodos multicriterio discreto se identifican con problemas donde el número de alternativas a considerar por parte del centro decisor es finito y normalmente no muy elevado. El interés práctico de los problemas multicriterio discreto (multiatributo) resulta evidente. En efecto, existen multitud de contextos decisionales en los que un número reducido de alternativas o elecciones posibles deben evaluarse basándose en varios atributos o criterios.

9.1 Método de los pesos promedios ponderados.

Dentro de los métodos multiatributos se encuentra el Método de los pesos promedios ponderados (Anexo 4) según Delgado (2008) donde:

A= diferentes alternativas.

C= criterios de decisión.

rij= valor de la Alternativa j en función del Criterio i

Wi= peso del Criterio i

Sj = valor esperado para la Alternativa j

Este método constituye una manera rápida y sencilla para identificar la alternativa preferible en un problema de decisión multicriterio a través de los siguientes pasos (Anexo 5) y sus técnicas:

Identificar el problema a resolver.
Identificar las alternativas de decisión.
Determinar criterios a emplear en la toma de la decisión. (Tormenta de ideas)
Normalizar la matriz de criterios. (Método de la transformación a escala)
Asignar peso a cada criterio de acuerdo al grado de importancia: (Procesos Analíticos Jerárquico (PAJ) para el cual Saaty propone aplicar los valores numéricos que se muestran en el Anexo 6)
Calcular el valor esperado para cada alternativa.
Seleccionar la alternativa de mayor valor esperado.

Roche, H. y Vejo, C. (2005) plantean que en ocasiones los problemas de decisión tienen que ver con 2 o más criterios, los cuales están en conflicto entre sí en el momento que el decisor busca identificar la mejor alternativa. Esto hace que para alcanzar la meta de seleccionar la alternativa prioritaria es necesario un trueque entre los múltiples criterios.

En esta clase se introducen dos métodos multicriterios de apoyo a la decisión gerencial:

Método del Scoring.
Método de Análisis Multicriterio conocido como el Proceso de Análisis Jerárquico (AHP).

Ambos métodos, parten de la base que el decisor debe establecer la importancia relativa de cada uno de los objetivos para luego definir una estructura de preferencias entre las alternativas identificadas. El resultado final resulta en una clasificación de las alternativas, indicando la preferencia general asociada a cada una de ellas, lo que permite identificar la mejor alternativa a recomendar.

9.2 Método del SCORING

El método del Scoring es una manera rápida y sencilla para identificar la alternativa preferible en un problema de decisión multicriterio.

Las etapas del método son los siguientes:

Identificar la Meta General del Problema.
Identificar las Alternativas.
Listar los Criterios a emplear en la toma de decisión.
asignar una ponderación para cada uno de los Criterios.
Establecer en cuanto satisface cada Alternativa a nivel de cada uno de los Criterios.
Calcular el Score para cada una de las Alternativas.
Ordenar las Alternativas en función del Score. La Alternativa con el Score más alto representa la Alternativa a recomendar.

Modelo para Calcular el Score:

S_j = ∑w_ir_ij

Donde:

r_ij = rating de la Alternativa j en función del Criterio i

w_i= ponderación para cada Criterio i

S_j = Score para la Alternativa j

9.3 ANÁLISIS MULTICRITERIO: Modelo Proceso Analítico Jerárquico (AHP, Thomas Saaty)

El método AHP es un procedimiento diseñado para cuantificar juicios u opiniones gerenciales sobre la importancia relativa de cada uno de los criterios en conflicto empleados en el proceso de toma de decisión.

Las 8 etapas del método AHP son las siguientes:

Descomponer el Problema de Decisión en una jerarquía de elementos interrelacionados, identificando:

(a) la Meta General,

(b) los Criterios (i=1,2,…m)

Para cada uno de los “m” Criterios repetir las Etapas (2) a (5):

Desarrollar la Matriz de Comparación por Pares (MCP) de Alternativas para cada uno de los criterios estableciendo el rating de importancia relativa entre ambas Alternativas consideradas.

El Rating se establece a partir de la escala siguiente:

1= igualmente preferida

3= moderadamente preferida

5= fuertemente preferida

7= muy fuertemente preferida

9= extremadamente preferida

Pueden asignarse los valores intermedios 2, 4, 6, 8. Un rating recíproco (ej. 1/9, 1/7, 1/5, 1/3,…) se aplica cuando la segunda alternativa es preferida a la primera. El valor 1 es siempre asignado a la comparación de una alternativa con si misma.

Desarrollar la Matriz normalizada (MCN) dividiendo cada número de una columna de la Matriz de Comparación por pares por la suma total de la columna.
Desarrollar el Vector de Prioridad para el Criterio calculando el promedio de cada fila de la Matriz Normalizada. Este promedio por fila representa el Vector de Prioridad de la Alternativa con respecto al criterio considerado.
La Consistencia de las opiniones utilizadas en la Matriz de Comparación por pares puede ser determinada a través del cociente de consistencia (RC). Un CR inferior a 0.10 es considerado aceptable. Para aquellos casos en que CR>0.10, las opiniones y juicios deberán ser reconsiderados.
Luego de que la secuencia (2)-(3)-(4)-(5) ha sido ejecutada para todos los criterios, los resultados obtenido en (4) son resumidos en una Matriz de Prioridad (MP), listando las Alternativas por fila y los Criterios por Columna.
Desarrollar una Matriz de Comparación de Criterios por pares de manera similar a lo que se hizo para las Alternativas en (2)-(3)-(4).
Desarrollar un Vector de Prioridad Global multiplicando el vector de prioridad de los Criterios (7) por la Matriz de prioridad de las Alternativas (6).

Determinación del Cociente de Consistencia.

Para cada Línea de la Matriz de Comparación por pares, determinar una suma ponderada en base a la suma del producto de cada celda por la prioridad de cada alternativa correspondiente.
Para cada Línea, dividir su suma ponderada por la prioridad de su Alternativa correspondiente.
Determinar la media λ_max del resultado de la etapa (2.)
Calcular el índice de consistencia para cada Alternativa

CI = λ_max – n

n – 1

Determinar el índice RI de la tabla siguiente:

Total de Alternativas (n)	Índice Aleatorio (RI)
3	0.58
4	0.90
5	1.12
6	1.24
7	1.32
8	1.41

Determinar el Cociente Consistencia (CR):

CR = CI/RI

Hasta aquí se han plasmado diversos criterios de autores en cuanto a los modelos Multicriterios, de manera general no se pueden lograr soluciones que optimicen todos los atributos a que alcancen todos los objetivos o metas, sino soluciones eficientes o de compromiso que permitan valores aceptables para el decisor.

9.4 Ejemplo del Modelo Multicriterio para la toma de decisiones: Método del

Un graduado de la Universidad de Ciego de Ávila en la carrera de Contabilidad y Finanzas ha recibido las siguientes ofertas de empleo:

de Subdirector económico en la Empresa de Ferrocarriles de Ciego de Ávila,
de Contador principal en el Hotel Sol Cayo Coco en el destino Jardines del Rey,
de Auditor en la Contraloría Provincial de Ciego de Ávila.

El recién graduado maneja múltiples criterios para tomar una decisión al respecto entre los cuales: el puesto de Subdirector económico es la mejor oportunidad para el avance profesional a largo plazo; pero prefiere vivir en Morón y considera a su vez que la Contraloría presenta el mejor estilo y ética administrativa, para lo cual se aplica en la determinación de la decisión el Método Multicriterio de SCORING.

Siguiendo los pasos establecidos anteriormente (Acápite 9.2):

Seleccionar la mejor Oferta de Empleo.
Alternativas: Subdirector económico en la Empresa de Ferrocarriles de Ciego de Ávila, Contador principal en el Hotel Sol Cayo Coco, Auditor en la Contraloría Provincial de Ciego de Ávila.
Criterios: Avance de la Carrera, Localización, Estilo y ética administrativa, Remuneración, Prestigio, Seguridad en el empleo y Calidad en el trabajo.
Asignación de una ponderación para cada Criterios mediante el empleo de un escala de 5 puntos:

1 = muy poco importante

2 = poco importante

3 = importancia media

4 = algo importante

5 = muy importante

Criterios	Ponderación w_i
Avance de la Carrera	5
Localización	3
Estilo administrativo	4
Remuneración	3
Prestigio	2
Seguridad en el empleo	4
Calidad en el trabajo	5

Establecer el rating de satisfacción para cada Alternativa empleando una escala de 9 puntos.

1 = extra bajo 5 = medio 9 = extra alto

2 = muy bajo 6 = poco alto

3 = bajo 7 = alto

4 = poco bajo 8 = muy alto

No.	Criterios	Subdirector económico Ferrocarriles	Contador principal Hotel Sol Coco	Auditor Contraloría
		r_i1	r_i2	r_i3
1	Avance de la Carrera	8	6	4
2	Localización	3	8	7
3	Estilo administrativo	5	6	9
4	Remuneración	6	7	5
5	Prestigio	7	5	4
6	Seguridad en el empleo	4	7	6
7	Calidad en el trabajo	8	6	5

Calcular la Ponderación para cada Alternativa

No.	Criterios	Ponderación w_i	Subdirector económico Ferrocarriles	Contador principal Hotel Sol Coco	Auditor Contraloría
			r_i1	r_i2	r_i3
1	Avance de la Carrera	5	8	6	4
2	Localización	3	3	8	7
3	Estilo administrativo	4	5	6	9
4	Remuneración	3	6	7	5
5	Prestigio	2	7	5	4
6	Seguridad en el empleo	4	4	7	6
7	Calidad en el trabajo	5	8	6	5
	SCORE S^j		157	167	149

La Oferta de “Contador principal Hotel Sol Coco” obtiene la Ponderación más alto de S^j =167, y por lo tanto representa la mejor Alternativa a recomendar.

10. Modelos econométricos. Análisis de Regresión y Series Cronológicas. Su empleo en la Toma de Decisiones. Ejemplos.

Como se ha mencionado hasta el momento son varios los métodos económicos matemáticos que se utilizan en la toma de decisiones, siendo de gran importancia la utilización de modelos econométricos, teniendo en cuenta que dan la posibilidad de realizar predicciones de diferentes situaciones que permitan en algún grado controlar la evolución del sistema y tomar la decisión que se necesite.

10.1 Modelos econométricos.

La Econometría no debe ser solamente considerada como sinónimo de aplicación de las matemáticas a la economía. La experiencia ha mostrado que cada uno de estos tres puntos de vista, el de la estadística, la teoría económica y las matemáticas es necesario, pero por si misma no es condición suficiente para una comprensión real de las relaciones cuantitativas en la vida económica moderna. Es la unión de los tres aspectos lo que constituye una herramienta de análisis potente, es esta unión lo que constituye la Econometría, cuyo objetivo central explicar a través de modelos los planteamientos o hipótesis que surgen de la economía teórica.

Para la formulación de un modelo econométrico se requiere:

De la teoría económica que se debe analizar.
Determinar las variables que intervienen en el estudio asociado a la teoría.
Determinar las relaciones que existen entre las variables.
Definir el objeto de estudio del modelo que exprese el comportamiento empírico de la teoría económica.

Clasificación de los modelos econométricos:

Modelos lineales (en cuanto a los parámetros o en cuanto a las variables):

-Lineales en cuanto a los parámetros:

Regresión lineal.

-Lineales en cuanto a las variables: se refiere a que las variables son las que están elevadas a la primera potencia.

Modelos no lineales que pueden ser transformados en lineales:

-Función de Producción de Cobb Douglas.

-Exponencial

-Modelo Potencial.

-Recíproco.

Modelos no lineales que no pueden ser transformados a lineales:

Otras clasificaciones son:

Mediante la toma de información: Estático y Dinámico.
Atendiendo al número de ecuaciones planteadas: Modelo Uniecuacional y Ecuaciones Simultáneas.

El análisis econométrico sigue los siguientes pasos de acción:

Enunciado de la teoría.
Especificación del modelo econométrico.
Estimación de los parámetros del modelo escogido.
Verificación o inferencia estadística.
Predicciones o pronósticos.
Formulación de políticas o utilización del modelo como medida de control.

Estos modelos podrán representarse y verificarse a través de las estadísticas, lo que permitirá realizar los pronósticos correspondientes y tomar las medidas necesarias en años posteriores, siendo de vital importancia en el proceso de toma de decisiones, para lo cual se han desarrollado diferentes software informáticos como el SPSS.

En general, los modelos econométricos son utilizados como una herramienta de análisis que ayuda en la toma de decisiones tanto a nivel económico general (macro) como en el ámbito de la dirección de empresas (micro).

10.1.1 Análisis de regresión.

La mayoría de los problemas (económicos ó no) involucran a más de una variable relacionadas para lo cual se desea generalmente lograr una expresión funcional que exprese dicha relación.

El análisis de Regresión proporciona un modelo econométrico que relaciona los valores de una variable dependiente o respuesta con los valores de al menos una variable independiente o factor.

Los métodos de regresión se usan para:

Determinar la mejor relación funcional entre las variables en estudio.
La predicción de valores.
Definir los parámetros de un modelo determinístico.
Discriminar entre varios modelos.

El Análisis de Regresión se relaciona con el Análisis de Correlación, cuyo objetivo fundamental es la medición del grado de asociación lineal que puede existir entre dos ó más variables, es decir, medir la fortaleza de asociación entre las variables numéricas.

Si se expresa una variable “y”: denominada variable dependiente, sólo en función de una variable explicatoria “x” se estará en presencia de la regresión simple, y será múltiple si en la relación hay más de una variable independiente, o sea:

Y = f (x) regresión simple

Y = f (x1, x2, … , xk) regresión múltiple

Los modelos de Regresión se clasifican en:

Modelos de Regresión Lineales.

Regresión Lineal Simple.
Regresión por la Vía Matricial.
Regresión Lineal con dos variables independientes.
Regresión Lineal Múltiple.

Modelos de Regresión no Lineales.

Resumiendo, estos modelos tienen como característica general que relacionan variables internas o externas con los niveles de demanda, lo que brinda una visión amplia del sector. Los costos que implican son de medios a bajos y usualmente requieren de equipo de cómputo. A su vez son más útiles para elaborar pronósticos a mediano plazo de productos o servicios existentes y para el diseño de estrategias de marketing, producción y contratación de personal.

A continuación se explicará el método de Regresión Lineal Simple y se ejemplificará.

10.1.1.1 Regresión Lineal Simple.

En la regresión simple, se considera que “y” es siempre una variable aleatoria (dependiente), mientras que “x” es una variable independiente que se considera de valores controlados o elegidos de antemano por el investigador. A la variable “x” se le denomina también variable explicatoria ó variable exógena o regresor.

La relación que se da entre las variables es una Función Lineal buscando la línea recta que mejor se ajusta a los datos.

Modelo General de Regresión Lineal donde sólo se maneja una variable independiente, por lo que sólo cuenta con dos parámetros.

El residuo es la diferencia entre el valor observado y el valor estimado:

Residuo =

El Error Estándar del Estimado, es decir, la desviación estándar de la variación de las observaciones alrededor de la Línea de Regresión se calcula:

10.1.1.2 Ejemplo del modelo de Regresión Lineal Simple.

La Empresa La Cuba desea proyectar la producción total teniendo en cuenta el uso de un nuevo fertilizante para el año 2016, para lo cual brinda la siguiente información donde se representa la producción agraria (X, ton) y la cantidad de fertilizantes utilizados (Y, litros) de una muestra de los 12 meses del año.

Para cada mes se tomó la producción agraria realizada y el fertilizante utilizado en la misma, resultando:

X	Y
152	50
155	61,5
152	54,5
155	57,5
157	63,5
152	59
157	61
165	72
162	66
178	72
183	84
178	82

Con estos datos vamos a plantear una ecuación de regresión simple que nos permita pronosticar la utilización del fertilizante de acuerdo a la producción.

Primeramente se calcula los coeficientes a y b.

b = 1/12*1226.1253 = 0,8688

1/12*1411,1354

a = Ym – (b * Xm)

a = 64,5056 – (0,8688*161,8168) = -76,0959

La ecuación de regresión estimada es:

Ŷ = a+b X

Ŷ = -76,0959 + 0,8688 X

El valor de b = 0.8688 indica el incremento de la producción agraria en toneladas, en promedio, por cada litro de aumento de fertilizante utilizado.

El valor de a, no tiene interpretación práctica en el ejemplo, se interpretaría como el valor obtenido, en promedio, para la producción agraria Y, cuando no se utiliza fertilizante.

Utilizando la ecuación de regresión para estimar o predecir valores de la variable Y, teniendo en cuenta una producción agraria de 160 toneladas:

Ŷ = -76,0959 + 0,8688 X

Ŷ = -76,0959 + 0,8688 (160) = 62.9121 litros de fertilizantes

Coeficiente de correlación:

R = 1226.1253 = 0.9372

……………………………………….37,5651* 34,8267

El coeficiente de correlación es igual a 0,9372, indicando una relación relativamente fuerte entre las variables.

Coeficiente de determinación:

R² =0.8783

El estadístico R-cuadrado indica que el modelo explica un 87.83 % de la variabilidad en Y, es decir, de las variaciones que ocurren en la utilización de los fertilizantes se explicarían por las variaciones en la variable producción agraria.

10.1.2. Series cronológicas.

Cuando hablamos de una secuencia de valores observados a lo largo del tiempo, y por tanto ordenados cronológicamente, la denominamos, en un sentido amplio, serie temporal. Resulta difícil imaginar una rama de la ciencia en la que no aparezcan datos que puedan ser considerados como series temporales. Si conocidos los valores pasados de la serie, no fuera posible predecir con total certeza el próximo valor de la variable, decimos que la serie es no determinista o aleatoria, y lógicamente es de estas de las que se ocupa el cuerpo de doctrina denominado: Análisis de “Series Temporales“ o “Series Cronológicas”.

Por tanto, una serie temporal, serie de tiempo o serie cronológica, pues de cualquiera de estas formas puede llamársele, se define como el conjunto de mediciones sobre el estado de una variable (el evento de salud considerado) ordenados en el tiempo.

Las series de tiempo o cronológicas tienen como característica que establecen relaciones entre el tiempo y los niveles de demanda. Su costo tiende a ser bajo, excepto para algunas técnicas como Box-Jenkins, que implica un software un tanto oneroso.

Igualmente en cuanto al horizonte se utilizan para el corto y mediano plazos y se aplican al manejo de inventarios, control de precios, programas de promociones y para considerar movimientos estacionales o cíclicos de la demanda. Requieren el uso de equipo y paquetes de cómputo.

Los objetivos del análisis de series temporales son diversos, pudiéndose destacar la predicción, el control de un proceso, la simulación de procesos y la generación de nuevas teorías Físicas, Biológicas, Económicas, etc.

Es necesario destacar el concepto de predicción como la estimación de valores futuros de la variable en función del comportamiento pasado de la serie y se teniendo en cuenta el horizonte de tiempo futuro que cubre, por lo que el horizonte de predicción puede tomar 3 categorías: Corto plazo, Mediano plazo y Largo plazo.

Las series temporales pueden clasificarse según la forma en que se ofrecen los valores de las mediciones en dos tipos:

Continuas: cuando los valores se ofrecen de forma permanente, de manera tal que cada uno de ellos representa el estado de la variable en un instante, el cual puede ser tan pequeño como teóricamente se quiera suponer.
Discretas: cuando los valores se ofrecen para intervalos de tiempo, generalmente homogéneos y donde representan la magnitud acumulada del estado de la variable durante ese intervalo.

La metodología tradicional para el estudio de series temporales es bastante sencilla de comprender, y fundamentalmente se basa en descomponer las series en varias partes: tendencia, variación estacional o periódica, y otras fluctuaciones irregulares.

Tendencia

Es la dirección general de la variable en el período de observación, es decir el cambio a largo plazo de la media de la serie.

Cuando se desea conocer la evolución de una variable en el largo plazo, el estudio de la tendencia se convierte en un factor relevante.

Para obtener la tendencia es necesario proceder a su aislamiento. Esto se realiza en función de los siguientes objetivos básicos: Para proyectar los valores futuros de la variable y para eliminar la tendencia calculada para la serie, y estudiar el comportamiento de los restantes componentes.

La ecuación de la tendencia puede ser lineal o curvilínea (parábola, exponencial).

Dentro de los métodos para determinar la Tendencia se encuentran el Método Gráfico, el Método de las Media Móviles y el Método de los Mínimos Cuadrados.

Los medios más utilizados para detectar y eliminar la tendencia de una serie se basan en la aplicación de filtros a los datos. Un filtro no es más que una función matemática que aplicada a los valores de la serie produce una nueva serie con unas características determinadas, dentro de los que se encuentran las medias móviles.

Estacionalidad

Corresponde a fluctuaciones periódicas de la variable, en periodos relativamente cortos de tiempo.

Las variaciones estacionales de una serie cronológica, son aquellas fluctuaciones que se repiten regularmente dentro del año.

El aislamiento del componente estacional, se funda en los siguientes objetivos: para identificar los valores estacionales, que complementan la estimación de valores futuros a través de la tendencia y para estudiar el componente cíclica de la serie desestacionalizada.

Al proceso que consiste en eliminar la componente estacional se le conoce como “desestacionalización”.

Si se considera un esquema multiplicativo, habrá que dividir cada dato de la serie por su correspondiente índice de variación estacional, expresado en tantos por uno.
Si el esquema es aditivo, a cada valor observado se le resta la diferencia estacional correspondiente.

Una serie desestacionalizada refleja, por tanto, el comportamiento de la serie original libre de la perturbación estacional.

Otras fluctuaciones irregulares.

Después de extraer de la serie la tendencia y variaciones cíclicas, nos quedará una serie de valores residuales, que pueden ser o no totalmente aleatorios. Volvemos a estar como en el punto de partida, pues ahora también nos interesa determinar si esa secuencia temporal de valores residuales puede o no ser considerada como aleatoria pura.

Otros autores como Coutin (2001) añaden a las partes anteriores otros conceptos:

Ciclo (C).

La variación cíclica también es periódica, aunque los intervalos de tiempo involucrados son mucho más largos, este componente solamente puede apreciarse, de existir, en series muy extensas.

Aleatoriedad (A).

Se trata del movimiento irregular de la serie determinado por el azar, impredecible, accidental. El enfoque clásico atribuye la presencia de este elemento en el comportamiento de la variable a errores de observación, medición o transmisión de los datos y por lo tanto imposible de modelar en ese contexto. Tradicionalmente se obtiene por exclusión de los otros y se le llama “residuo aleatorio”.

El análisis de series cronológicas, se realiza a través de dos modelos básicos:

Modelo Aditivo Yt = Tt + St + Ct + Et
Modelo Multiplicativo Yt = Tt * St * Ct * Et

Donde:

Yt – Variable estudiada

Tt – Tendencia

St – Variaciones estacionales

Ct – Fluctuaciones cíclicas

Et – Sucesos aleatorios o irregulares

Resumiendo diremos que el movimiento de una serie cronológica se compone de la superposición de:

Un movimiento de traslación (tendencia), T (t).
Un movimiento vibratorio (variación estacional), E(t).
Un movimiento de oscilación (variación cíclica), C(t).
Un movimiento perturbador (variación aleatoria), A(t).

Existen numerosos métodos para trabajar con las series temporales y la utilización de uno u otro está en dependencia de los objetivos propuestos y de las características de las mismas. No se recomienda hacer más complejo de lo necesario este proceso pues si lo que se pretende demostrar puede lograrse mediante un método simple, éste resultará mejor que uno más complejo, sobre todo, si no se poseen los recursos tecnológicos que generalmente son necesarios para el empleo de métodos más complicados.

Clasificación de los métodos de series cronológicas:

Proyección de Línea Recta: predice la demanda a partir de una línea recta en la que se han incluido los datos de demanda a través del tiempo.
Promedios móviles: promedia los valores de demanda reciente para predecir la demanda futura.
Naive: es la aplicación de un supuesto simple: en el próximo periodo se repetirá la demanda actual.
Suavización exponencial: consiste en estimar la demanda del próximo período basándose en una combinación de indicadores de la demanda reciente y de los pronósticos pasados.
- Método de alisamiento exponencial simple.
- Método de alisamiento Holt – Winter sin estacionalidad.
- Método de alisamiento Holt – Winter con estacionalidad (Multiplicativo).
- Método de alisamiento Holt – Winter con estacionalidad (Aditivo).
Descomposición clásica: es la predicción de la demanda esperada a partir de la tendencia, estacionalidad y ciclicidad que se han registrado en el pasado (en los dos últimos años, por ejemplo).
Box-Jenkins: cruza varias series de tiempo para obtener otra serie de tiempo (o más de una) que permita estimar la demanda futura.

A continuación se explicará el método de Alisamiento exponencial simple y se ejemplificará.

10.1.2.1 Alisamiento exponencial simple.

El suavizamiento exponencial recibe este nombre porque los pesos o ponderaciones que se asignan a períodos anteriores para formar el pronóstico disminuyen en forma exponencial. Es decir, las ponderaciones decrecen con rapidez conforme el período es más antiguo.

Este método genera pronósticos acertados para muchas variables de series de tiempo y reconoce el impacto decreciente de períodos cada vez más lejanos en el pasado, permite suavizar los datos reduciendo el grado de variación de ellos, y dar mayor importancia a casi todas las cifras recientes.

Es un procedimiento que puede ser muy útil para la descripción de la tendencia, particularmente en serie con grandes oscilaciones y más útil aún en la elaboración de pronósticos, está diseñada especialmente para emplearse en el análisis de Series de Tiempo y con la ventaja que no se sustenta en supuestos.

El método de Alisamiento de lo que trata es de suavizar la serie y expresar el pronóstico como una combinación ponderada de dos cantidades:

el valor de la variable real en el período anterior y
el pronóstico hecho para ese período de la variable.

Es usual emplear esta técnica cuando el horizonte de pronóstico es a corto plazo.

Se tiene en cuenta un valor de ponderación (constante de suavización = α) que determina en qué medida el período más reciente contribuye al pronóstico.

La fórmula sería:

Pronóstico de la variable para el siguiente año

= α

El valor real de la variable del período anterior

+ (1- α)

Pronóstico para el año anterior de la variable

Significando esto que el pronóstico está basado en el 20% del valor reciente Y_t y el 80% de lo pronosticado para el período actual Ŷ t

Si se toma como valor de a el valor extremo, es decir, cuando a = 0 entonces:

entonces se pronostica para el próximo período el mismo valor que lo que se pronosticó para el período corriente

Mientras que si a = 1 entonces

sólo se considera el más reciente valor de Y.

Así mientras más alto es a es más sensible el pronóstico a los cambios del valor reciente de Y, y el alisado será menor. Y mientras más cercano este a de cero, será mayor el alisamiento.

Un a pequeño se puede usar con datos de series de tiempo que son relativamente estables. Si la serie cambia rápidamente a debe ser grande, porque asigna pesos grandes a las observaciones más recientes. Esta recomendación está sustentada en que tanto mayor sea el valor de a menor es el suavizamiento que se logra en la serie. Un a grande implica un reducido alisado, mientras que un a pequeño conlleva un fuerte alisamiento en la serie.

Los valores más comunes de a están entre 0.01 y 0.60, sin embargo, la determinación de a generalmente está basada en el valor que minimice la Suma de los Cuadrados de los residuos.

Los pesos que se usan son, para los datos más recientes, disminuyendo este, para los datos más antiguos.

El que será un valor que estará comprendido entre (0 <a< 1).

Cuando a está cercana a 1, la información más reciente afectará más al nuevo pronóstico.

Cuando el valor de está cercano a 0, el nuevo pronóstico será muy parecido a la observación más antigua.

Es por ello que la constante de suavizamiento,, es la clave del uso del suavizamiento exponencial. Si es necesario que los pronósticos sean estables y que se suavicen las variaciones aleatorias, se requiere de un pequeño. Si se desea una respuesta rápida a los cambios reales en el patrón de observaciones, un valor grande de es apropiado.

La mayor parte de los paquetes de suavizamiento exponencial encuentra la constante de suavizamiento óptimo (a) mediante la minimización de la suma de cuadrados residual o del error: SC_E = claro que esto es desde el punto de vista matemático lo que no quiere decir definitivamente, que ese es el mejor valor de la constante de suavizamiento, ya que el que puede conocer esto es el especialista, porque es el que conoce el comportamiento futuro que puede tener la serie.

En el modelo de alisamiento exponencial simple, el pronóstico del próximo y todos los períodos siguientes se determina ajustando el pronóstico del período corriente, por una porción de la diferencia entre el pronóstico y el valor actual. Por lo que si las predicciones recientes están sujetas a errores grandes, los nuevos pronósticos tomarán esto en consideración.

Por todo ello se puede concluir que en la suavización exponencial los pesos asignados a los valores observados, disminuyen al paso del tiempo, por lo que cuando se hacen cálculos, el valor observado más reciente recibe el peso más alto, el valor observado inmediatamente anterior, recibe el segundo valor más alto y así sucesivamente, recibiendo el peso más bajo el valor observado inicialmente.

Las razones para el uso del alisamiento exponencial son: entre otros está que para pronosticar un período sólo es necesario el valor actual de la variable, el pronóstico para el período corriente (ó el período anterior de la variable) y un factor de ponderación llamado constante de alisamiento, además, la mayoría de los software, como el SPSS, incluyen módulos de alisamiento, y se ha demostrado que los pronósticos obtenidos son precisos.

Por todo ello se puede plantear que el alisamiento exponencial es quizás el modelo más usado en series de tiempo. Es una técnica extremadamente simple de entender y aplicar. Los nuevos pronósticos se derivan ajustando los pronósticos previos, y los pronósticos pueden revisarse continuamente basándose en experiencias previas

Ventajas de la aplicación de este modelo:

Son muy fáciles de obtener con un sistema en computadora.
Se requiere de un mínimo de información, comparada con otros modelos de pronósticos
A las observaciones recientes se les asignan mayor peso.
Reacciona más rápidamente a cambios en el patrón de los datos (condiciones económicas).
Un procedimiento que puede ser muy útil para la descripción de la tendencia, particularmente en series con grandes oscilaciones.
Esta técnica, la de alisamiento exponencial fue diseñada específicamente para emplearse en el análisis de series de tiempo, y no se sustenta en supuestos, como es el caso del método de los mínimos cuadrados.

Se debe plantear además de que existe el criterio de que el Método de Alisamiento exponencial simple debe utilizarse en lo fundamental en series de tiempo, que no presente tendencia ni estacionalidad.

10.1.2.2. Ejemplo del modelo de Alisamiento exponencial simple.

La Empresa Cepil se dedica a la producción de cepillos y otros artículos plásticos. Ha acumulado los datos de la demanda de cepillos del año 2015, los que se presentan a continuación:

Meses	Y_t (MU)
Enero	37
Febrero	40
Marzo	41
Abril	37
Mayo	45
Junio	50
Julio	43
Agosto	47
Septiembre	56
Octubre	52
Noviembre	55
Diciembre	54

Y desean que se estimen los pronósticos para el 2016, a partir del Alisamiento exponencial simple, utilizando un a = 0.30 y donde Y_t = Demanda de cepillos dentales, siendo el pronóstico del mes de enero para el 2015 igual al 2014.

Para lo cual se utiliza:

Alisamiento exponencial simple indicándonos

Estimación del período t + 1 = a(dato del período anterior) + (1-a) (estimación del período anterior)

El valor inicial del pronóstico es la primera observación del actual, es decir, de los datos que se tienen, esto es, = Y_t.

Se ha planteado que el valor inicial del pronóstico, es el primer dato ó el primer valor real del período, sin embargo, hay autores que consideran que se puede tomar un valor arbitrario para el pronóstico anterior. Este valor debe estar en el mismo intervalo que los valores reales de la serie de tiempo, otros toman un promedio de las primeras observaciones. De hecho, el valor escogido para el pronóstico anterior no es crítico. Porque una vez preparados varios pronósticos para períodos futuros, la influencia de este valor habrá decrecido exponencialmente y no tendrá un efecto sustancial en el pronóstico.

Como los datos son mensuales, entonces t = enero

Como se aprecia, el valor estimado para un momento dado depende de los valores inmediatos anteriores, reales y estimados, ponderados en magnitudes a y 1- a, respectivamente, y a su vez el estimado dependió de los valores reales y estimados previos.

Y de esta forma se han hallado los pronósticos para cada período analizado, que en este caso corresponde a meses (Ver gráfico en Anexo 7). Es bueno significar que se ha realizado un ejercicio con datos muy sencillos para no involucrarse en grandes operaciones.

10.2. Importancia de los modelos econométricos para la toma de decisiones.

Existen muchas razones para utilizar los modelos econométricos, por ello son de gran importancia en nuestro medio pues entre otras cosas sirven para:

Describir las características más sobresalientes de cualquier evento en el tiempo.
Predecir el comportamiento futuro de un evento según su conducta pasada.
Estudiar el mecanismo que genera la serie.
Evaluar impacto de las intervenciones realizadas sobre determinado problema.
Contribuir a la prevención de problemas.
Controlar la calidad de las decisiones tomadas.
Planificar recursos.

Los modelos econométricos pueden usarse con fines predictivos, es decir, para predecir el valor de la variable dependiente en períodos futuros.

Los pronósticos del futuro son datos importantes para la toma de decisiones administrativas. Los gerentes de comercialización necesitan pronósticos de ventas futuras para tomar las decisiones sobre precios, contratación, promoción y distribución. Los gerentes de producción necesitan pronósticos respecto del tiempo de producción para tomar decisiones sobre compras, personal, programación e inventarios. Los gerentes de contabilidad y finanzas requieren pronósticos de flujo de caja con el objetivo de tomar decisiones sobre préstamos, inversiones a corto plazo y financiamiento en general.

CONCLUSIONES

Dentro del entorno económico actual las organizaciones se ven en la obligación de mejorar sus procesos de toma de decisión día a día para afianzar su competitividad a través del empleo de los modelos económicos – matemáticos, satisfaciendo de la mejor forma a los usuarios con sus productos y servicios, y además hacer un uso más eficiente de los recursos.
La representación de un problema dado a través de los modelos económicos – matemáticos puede tomar diferentes formas y ser una ayuda invaluable para reunir y mostrar el problema en particular o los parámetros de la decisión. Un conocimiento básico de la teoría de la decisión ayudará a quienes la utilizan a tomar decisiones acertadas.
La ejemplificación de los modelos Multicriterios, Análisis de Regresión y Series cronológicas demostró su importancia en el proceso de toma de decisiones por su aplicación constante en la actividad empresarial.

BIBLIOGRAFÍA

S. y W. (2006). Análisis Cuantitativo y el Proceso de Toma de Decisiones.htm
B, M. (2001). La Toma de Decisión y su puesta en práctica.
B, M. (2001). La Toma de Decisiones. Disponible en: http://www.monografias.com/trabajos12/decis/decis2.shtml#ixzz3loyL4yJI
Bustos Farías, E. (2007). Análisis de decisiones.
Coutin Marie, G. (2001). Las Series Temporales. Ministerio de Salud Pública. Area de Higiene Y Epidemiología. Unidad de Análisis y Tendencias en Salud. La Habana.
Delgado Landa, A. (2008). La toma de decisiones empresariales con criterios múltiples. Disponible en http://www.monografias.com/trabajos66/toma-decisiones-empresariales/toma-decisiones-empresariales2.shtml#ixzz3logAtnRu
Fernández Ruiz, A. (). Decisiones Económicas.
Gallarher, Ch; Hugh, J. Watson. (1994). Métodos Cuantitativos para la toma de decisiones en administración. Litografía Ingramex. México. 621p.
Imbert Tamayo, J. (2002). Capítulo 6. Teoría de las Decisiones. “INVESTIGACIÓN DE OPERACIONES PARTE I: Un enfoque empresarial para la toma de decisiones”. Editorial Santiago de Cuba.
López Gutiérrez, N. y Martínez Pedregal, A. (2005, febrero) Contribución de los métodos cuantitativos en la formación de los profesionales. Ponencia presentada en el V Congreso Internacional Virtual de Educación, La Habana, Cuba.
Menguzzato, M. y Renau, J.J. (1995). “La dirección estratégica de la empresa. Un enfoque innovador del management”, Ariel, Barcelona.
Ministerio de Finanzas y Precios. (2005). Resolución 235. Normas Cubanas de Contabilidad e Información Financiera.
Pérez, T. (2010). Investigación de operaciones 3. Teoría de decisiones. Disponible en: https://www.gestiopolis.com/investigacion-de-operaciones-que-es-historia-y-metodologia/
Roche, H. y Vejo, C. (2005). Análisis multicriterio en la toma de decisiones. Métodos Cuantitativos Aplicados a la Administración.
Rodríguez-Uría, M. V.; Bilbao Terol, A.; Arenas Parra, M.; Pérez Gladish, B. y Antomil Ibias J (). Las matemáticas como soporte de las decisiones en economía y empresa. Departamento Economía Cuantitativa. Universidad de Oviedo.
Vitoriano, B (2007). TEORÍA DE LA DECISIÓN: Decisión con Incertidumbre, Decisión Multicriterio y Teoría de Juegos. Universidad Complutense, Madrid.
VI Congreso del PCC. (2011) Lineamientos de la Política Económica y social, capítulo I Modelo de gestión económica, Lineamiento 8.

Métodos del nivel teórico

Cita esta página

Escrito por:

Artículos Relacionados

Lógica de la modelación matemática simple para la Toma de Decisiones

Gestión de inventarios con demanda independiente en empresas comerciales y de servicios