Introducción
Dentro de esta investigación se planteó el objetivo de definir cada uno de los modelos de redes, empezando desde los conceptos más básicos como la definición de lo que sería un nodo que son las vértices utilizadas dentro de un modelo de red, un arco que podría ser la flecha o el conector de cada nodo dentro de la red, también las consideraciones a tomar para entender la estructura de una red, tales podrían ser como las direcciones que toman los arcos, pueden ser directas o indirectas.
Una vez entendidas las terminologías de las partes que conforman las redes, proseguimos con lo que sería cada uno de los modelos, el primero podría ser matriz de incidencia nodo-arco que sería una tabla que representa un modelo en la red, la técnica de árbol de expansión mínima, los pasos que hay que seguir para realizarlo, la técnica de flujo máximo, los pasos de la técnica, la técnica de la ruta más corta y los otros modelos de redes que serían, problemas de transporte, problemas del caminos más corto, camino critico en la planificación de proyectos de redes, problema de flujo de costo mínimo, análisis de sensibilidad para los modelos de redes, el problema de viaje del vendedor, también utilizando unos ejemplos para que los temas puedan quedar más claros.
Todos estos temas se explican más a detalle y con mejor entendimiento dentro del documento.
Modelos de redes
Un modelo de red es un modelo de transbordo con capacidades, el cual puede adoptar diversas formas, como el modelo de la ruta más corta y el modelo del flujo máximo y mínimo, el problema de árbol de alcance mínimo, método de camino crítico, entre otras aplicaciones de la planeación financiera y de producción.
La principal característica de un modelo de transbordo con capacidades es que es una red donde las ofertas están en los puntos de origen específicos, las demandas en los puntos de destino específicos y las alternativas de embarque se ofrecen por medio de los nodos intermedios, de manera que siguen rutas con capacidades definidas desde los orígenes hasta los destinos.
Terminología de redes
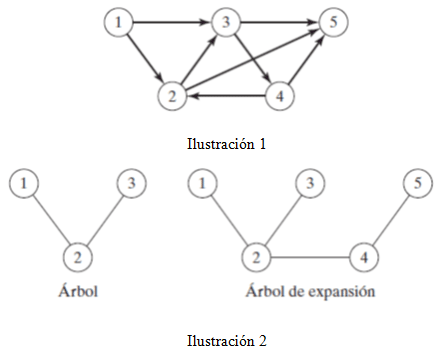
Una red se compone de un conjunto de nodos unidos por arcos (o ramas). La notación para describir una red es (N, A), donde N es el conjunto de nodos, y A es el conjunto de arcos.
N = {1, 2, 3, 4, 5}
A = {(1, 2), (1, 3), (2, 3), (2, 5), (3, 4), (3, 5), (4, 2), (4, 5)}
A continuación se presenta un diagrama de red y sus principales componentes.
¿Qué es un Nodo?
Es usualmente llamado vértice, o punto. Es usualmente representado por un círculo. En las redes de transporte, estos deberían ser las localidades o las ciudades en un mapa.
¿Qué es un Arco?
Es usualmente llamado borde o flecha. Este podría ser directo o indirecto. La cabeza es el destino, y la cola el origen. La cabeza y la cola son nodos que pueden estar tanto al origen como al final. En las redes de transporte, los arcos podrían ser los caminos, los canales de navegación en un río, o los patrones de vuelo de un avión. Los arcos proporcionan la conectividad entre los nodos. Una calle de una sola dirección podría ser representada por un arco, mientras que una calle de dos direcciones podría representada por un arco sin dirección o por dos arcos que apuntan a direcciones opuestas. Una red con n nodos podría tener tantos arcos como n! /[(n-2)! 2!] = n(n-1)/2. Si están dirigidos, este número pudiese ser doble. Este enorme número de arcos posibles es una de las razones del porque existen soluciones de algoritmos especiales para problemas de redes particulares.
En el nodo de la red comúnmente encontrarás un número con un signo positivo o negativo, el cual denota la oferta (+) y la demanda o requerimientos (-) del nodo.
Una ruta es un conjunto de arcos que unen dos nodos distintos, y que pasan a través de otros nodos en la red. Por ejemplo, en la Ilustración 1, los arcos (1,2), (2,3), (3,4) y (4,5) forman una ruta entre los nodos 1 y 5. Una ruta forma un ciclo o un bucle si conecta un nodo de vuelta a sí mismo a través de otros nodos. En la figura 6.1, los arcos (2,3), (3,4) y (4,2) forman un ciclo.
Consideraciones importantes:
- Las flechas/líneas de una sola dirección son arcos directos.
- Las líneas con flujo para ambas direcciones son arcos indirectos.
- Una red que tiene solamente arcos directos es una red directa.
- Una red que tiene arcos en ambas direcciones es una red indirecta. Una ruta directa del nodo i a la j es una secuencia de arcos conectados, por lo que es factible un flujo que pase a través de esa ruta.
- Una ruta indirecta de un nodo i a j es una secuencia de arcos conectados, cuyo sentido es de i a j o viceversa.
- Una ruta que empieza y termina en el mismo nodo es un ciclo.
- Si la red contiene como mínimo una ruta directa entre 2 nodos, se dice que están conectados. Para determinar cuál de las rutas de la red será elegida debemos considerar los costos y las capacidades a lo largo del recorrido de las rutas.
Modelos de redes versión 1
Matriz de incidencia nodo – arco
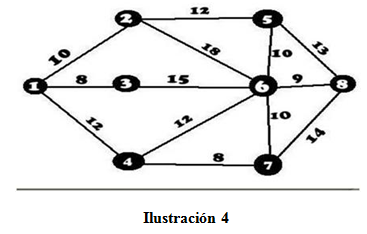
Es una tabla para representar los datos de las restricciones en un modelo de red. Cada arco de la red corresponde a una columna de la tabla. Cada nodo de la red corresponde a una fila de la tabla. Las columnas solo tienen dos entradas diferentes a cero: +1 y -1.
Una vez que hemos planteado el modelo de programación lineal, debemos encontrar la solución que programación lineal, debemos encontrar la solución que optimice la función objetivo.
- Podemos utilizar algún software de programación lineal como SOLVER o LINDO para encontrar la solución óptima.
Cierre
- La terminología y procedimiento para dibujar una red te servirán para aplicar los modelos de optimización, ya que al observar la Ilustración 3 es mucho más fácil identificar la ruta más corta o más larga, etc.
Modelo de redes versión 2
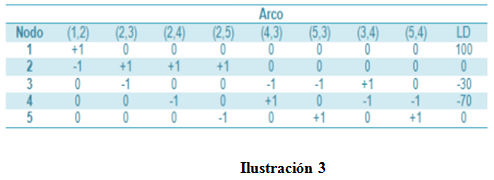
Técnica de árbol de expansión mínima
Este árbol vincula los nodos de una red valiéndose de la longitud mínima total de las ramas de conexión. Una aplicación común se presenta en la pavimentación de carreteras que unen poblaciones, o de forma directa, o que pasan por otras poblaciones. La solución del árbol de mínima expansión proporciona el diseño del sistema de carreteras.
Pasos Técnica de árbol de expansión mínima
- Seleccionar cualquier nodo de la red.
- Conectar este nodo al nodo más cercano que minimice la distancia total.
- Considerando todos los nodos que ahora están conectados, encontrar y conectar el nodo más cercano que no esté conectado.
- Si hay empate para el nodo más cercano, seleccionar uno arbitrariamente. Un empate sugiere que puede haber más de una solución óptima.
- Repetir el tercer paso hasta que todos los nodos estén conectados.
Ejemplo
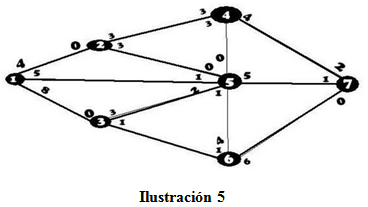
Roxie LaMothe propietaria de una gran granja criadora de caballos cerca de Orlando planea instalar un sistema de agua que conecte todos los establos y graneros. La ubicación de las instalaciones y las distancias entre ellas se muestran en la siguiente figura. Roxie debe determinar la forma más barata de suministrar agua a cada instalación.
La técnica del flujo máximo
- La técnica del flujo máximo determina lo más que puede fluir a través de una red.
4 pasos de la técnica del flujo máximo
- Elija cualquier trayectoria del inicio (original) a la terminación (destino) con algo de flujo. Si no existe alguna trayectoria con flujo, entonces se llegó a la solución óptima.
- Localice el arco el arco de la trayectoria con la capacidad de flujo más pequeña disponible.
- Llame C a esta capacidad. Ésta representa la capacidad máxima adicional que puede ser asignada a esta ruta.
- Por cada nodo que haya en esta trayectoria, disminuya la capacidad de flujo en la dirección del flujo en la cantidad C. Por cada nodo que haya en esta trayectoria, incremente la capacidad de flujo en la dirección inversa en la cantidad C.
Repita estos pasos hasta que ya no sea posible incrementar el flujo.
Ejemplo
PetroChem, una refinería de petróleo localizada sobre el río Mississippi al sur de Baton Rouge, Luisiana está diseñando una nueva planta para producir combustible diesel. La Ilustración 5 muestra la red de los centros de procesamiento principales junto con la velocidad de flujo existente. A la administración le gustaría determinar la cantidad máxima de combustible que puede fluir a través de la planta, del nodo 1 al nodo 7.
Técnica de la ruta más corta
Este problema determina la ruta más corta entre un origen y un destino en una red de transporte.
Pasos de la técnica de la ruta más corta
- Encuentre el nodo más cercano al origen. Coloque la distancia en una casilla junto al nodo.
- Encuentre el siguiente nodo más cercano al origen (planta) y coloque la distancia en una casilla junto al nodo. En algunos casos, se tendrán que revisar varias trayectorias para encontrar el nodo más cercano.
- Repita el proceso hasta que haya recorrido toda la red. La última distancia en el nodo final será la distancia de la ruta más corta. Es de notar que la distancia colocada en la casilla junto a cada nodo es la ruta más corta a este nodo. Se utilizan estas distancias como resultados intermedios para encontrar el siguiente nodo más cercano.
Ejemplo:
RentCar está desarrollando una política de reemplazo para su flotilla de automóviles en un horizonte de planeación de 4 años. Al inicio de cada año, un automóvil se reemplaza o se conserva en operación durante un año más. Un automóvil debe estar en servicio de 1 a 3 años. La siguiente tabla proporciona el costo de reemplazo como una función del año en que se adquiere un automóvil y los años en operación.
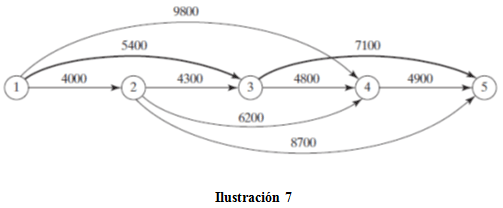
El problema puede formularse como una red en la que los nodos 1 a 5 representan el inicio de los años 1 a 5. Los arcos a partir del nodo 1 (año 1) pueden llegar a los nodos 2, 3 y 4 porque un automóvil puede estar en operación de 1 a 3 años. Los arcos a partir de los demás nodos pueden interpretarse del mismo modo. La longitud de cada arco es igual al costo de reemplazo. La solución del problema es equivalente a determinar la ruta más corta entre los nodos 1 y 5.
La Ilustración 6 muestra la red resultante. Utilizando TORA, 2 la ruta más corta es 1 S3 S5.
La solución indica que un automóvil adquirido al inicio del año 1 (nodo 1) debe reemplazarse después de 2 años al inicio del año 3 (nodo 3). El automóvil de reemplazo se mantendrá entonces en servicio hasta finales del año 4. El costo total de esta política de reemplazo es de $12,500
(= $5400 + $7100).
Modelo de redes versión 3
Tipos de Modelo de Redes
La familia de redes de los problemas de optimización incluye los siguientes prototipos de modelos: Problemas de asignación, camino crítico, flujo máximo, camino más corto, transporte y costo mínimo de flujos. Los problemas son establecidos fácilmente mediante el uso de arcos de redes y de los nodos.
Problemas de Transporte
Los modelos de transporten juegan un papel importante en la gerencia logística y en la cadena de insumos para reducir costos y mejorar servicios. Por lo tanto, el objetivo es encontrar la manera más efectiva en término de costos para transportar bienes. Un distribuidor que tiene “m” depósitos con un abastecimiento de productos a iith en ellos, debe enviar dichos productos a n centros minoristas geográficamente dispersos, cada uno con una demanda de clientes dada e j, la cual debe ser cubierta. El objetivo es determinar el mínimo costo posible de transporte dados los costos por unidad de transportar entre el ith depósito y el j Th centro minorista, el cual es Cij.
Problemas del Camino Más Corto
El problema es determinar la mejor manera de cruzar una red para encontrar la forma más económica posible desde un origen a un destino dado. Suponga que en una red dada existen m nodos y n arcos (bordes) y un costo Cij asociado con cada arco (i a j) en la red. Formalmente, el problema del camino más corto (CC) es encontrar el camino más corto (menor costo) desde el nodo de comienzo 1 hasta el nodo final m. El costo del camino es la suma de los costos de cada arco recorrido. Defina las variables binarias Xij, donde Xij=1 si el arco (i a j)es sobre el CC y Xij= 0 de lo contrario. Existen dos nodos especiales llamados origen y destino. El objetivo es encontrar el camino más corto entre el origen y el destino.
Camino Crítico en la Planificación de Proyectos de Redes
La gerencia exitosa de un proyecto ambicioso, ya sea de construcción, de transporte o financiero, descansan en una coordinación y planificación minuciosa de varias tareas. El Método de Camino (o trayectoria) Crítico (MCC) intenta analizar la planificación de proyectos. Esto posibilita un mejor control y evaluación del proyecto. Por ejemplo, queremos saber ¿Cuánto tiempo durará el proyecto?, ¿Cuándo se estará listo para comenzar una tarea en particular?, si la tarea no es completada a tiempo,
¿El resto del proyecto se retrasará?,
¿Qué tareas deben ser aceleradas (efectivas) de forma tal de terminar el proyecto antes?
Problema de Flujo de Costo Mínimo
Todos los problemas de red anteriores son casos especiales del problema de flujo de costos mínimo. Al igual que el problema de flujo máximo, este considera flujos en las redes con capacidades. Al igual que el problema del camino más corto, este considera un costo por flujo hacia un arco. Al igual que el problema de transporte, este permite múltiples orígenes y destinos. Por lo tanto, todos estos problemas pueden ser vistos como casos especiales del problema de flujo de costos mínimo. El problema es minimizar el costo total sujeto a la disponibilidad y la demanda de algunos nodos, y de la conexión superior de flujo a través de cada arco.
Análisis de Sensibilidad para los Modelos de Redes
La familia de un clásico problema de optimización de redes incluye los siguientes prototipos de modelos: asignación, camino crítico, flujo máximo, camino más corto, y transporte. A pesar de que es bien conocido que este tipo de problemas se pueden modelar como programación lineal, normalmente nunca se hace. Debido a la ineficiencia y complejidad relativa del método simplex (primal, dual y otras variaciones) para modelos de redes, este problema es tratado por uno de más de 400 algoritmos especiales. Esto conlleva a muchas dificultades. Las soluciones de los algoritmos no están unificadas y cada algoritmo usa una estrategia diferente para explorar la estructura especial de un problema específico. Adicionalmente, pequeñas variaciones en el problema tales como la adición de una restricción aparte, o índices múltiples, destruye la estructura especial y obliga a re comenzar el algoritmo. Además, estos algoritmos obtienen soluciones eficientes al costo de la astucia gerencial, como la solución final de estos algoritmos que no tienen la información suficiente para realizar un análisis de sensibilidad.
El Problema de Viaje del Vendedor
Un vendedor debe visitar las ciudades 1, 2,..N, y su viaje comienza y debe finalizar en Ciudad Hogar. Dejemos que Cij sea el costo de viajar de la ciudad y la ciudad j, el cual es dado. El problema es determinar una orden óptima para viajar las ciudades de tal forma que el costo sea mínimo. La maximización de flujos es un problema típico de la Investigación de Operaciones, el cual tiene muchas aplicaciones, por ejemplo el flujo vial en una ciudad, una red de aguas negras, una red informática, etc
Conclusión
Para concluir podemos decir que los arcos son los conectores de nodos dentro de cada red, estos modelos pueden tener una dirección directa o indirecta, que dentro de cada red puede haber múltiples conectores que sirven para unir varios nodos y asi crear rutas, dentro de cada red hay ciclos que unen nodos fuera de la ruta original.
Los modelos pueden ser representados mediante programas de la red, los de la segunda versión como la técnica de árbol de expansión mínima se utiliza para casos que son de distancias cortas o rutas pequeñas, la técnica de flujo máximo determina cuanto es lo más que puede fluir dentro de una red, la técnica de la ruta más corta nos sirve para determinar la ruta más corta desde nuestro nodo de origen y nuestra ruta de transporte.
Los modelos de redes tienen un uso común en ciertos aspectos laborales y que gracias a ellos podemos resolver problemas, y se pueden desenvolver en diferentes ámbitos facilitando las rutas que mejor convengan.
Esperemos que este artículo sea de gran utilidad y que los conceptos contenidos queden explicados de manera clara.
Referencias
- Hillier, F., Lieberman, G. (2006). Introducción a la Investigación de Operaciones. (8ª Ed.) México. McGraw Hill. ISBN 970-10-5621-3
- Oc,F, (2010), Modelos de redes-Investigación de Operaciones, recuperado de http://www.slideshare.net/FreddOc/modelos-de-redes-investigacin-de-operaciones
- Taha, H. A. (2012), Investigación de Operaciones, (9ª Ed.), México, Pearson Educación. ISBN: 978-607-32-0796-6
- Raffo, E. (1990), Investigación de Operaciones, Lima, Raffo Lecca Editores, Código de Biblioteca: 658.4034/T16