Por las particularidades de las empresas agroindustriales azucareras en lo que a tecnología se refiere, así como por las limitaciones en cuanto a recursos financieros para desarrollarse, la estrategia fundamental ha de centrarse en la reducción de los costos, y una vía está dada al reducir variabilidad en el proceso, elemento esencial que todavía hoy a nivel internacional constituyen un problema no resuelto fundamentalmente en las industrias de proceso, donde según Juran existen las mayores reservas, por lo que para Cuba es un reto, que implica salirse de lo tradicional en el proceder para análisis y control de proceso. En el trabajo se parte de un análisis estadístico tradicional que caracteriza las variables tecnológicas, evalúa el estado de control de proceso, para proseguir con la utilización de las series de tiempo, basado en la metodología de Box- Jenkins, que permite identificar los modelos que describen las variables estudiadas. La presencia de causas asignables de variación en los gráficos de control de los residuos del modelo ARIMA, permiten evaluar la cuantía de su efecto en la variabilidad del proceso, la identificación de los momentos que tales comportamiento ocurren y la posibilidad de atenuar tales efecto con la consiguiente reducción de variabilidad, además se procedió a la evaluación de las entradas al proceso. Todo ello con el objetivo de evaluar el efecto de la autocorrelación en el proceso de extracción de la empresa azucarera «Melanio Hernández».
Palabras claves: Series de tiempo estructuradas, Industria azucarera, proceso de extracción, calidad.
Introducción.
Para el ambiente de manufactura la ingeniería de calidad practicada, está cambiando rápidamente, son muchas las organizaciones que están enfrentando altas demandas, para lo cual se requiere la introducción de nuevos sistemas y nuevos productos.
Las transiciones de los sistemas se están convirtiendo en la parte más significativa de las operaciones generales y existe una presión incrementada para la ingeniería de la calidad así como otras actividades de manufactura para apoyar los objetivos económicos y la rentabilidad de la entidad, situación ésta que exige a la ingeniería de calidad el empleo de herramientas para enfrentarse a esos cambios así como a la intensa competencia internacional.
Debido a las particularidades de las empresas agroindustriales azucareras en lo que a tecnología se refiere, así como a las limitaciones en cuanto a recursos financieros para desarrollarse, las estrategias fundamentales han de centrarse específicamente en la reducción de los costos. Particular importancia, a los efectos de reducir los costos del azúcar y sus derivados, tiene la utilización racional de los recursos y capacidades de la empresa.
La Ingeniería de Control de Proceso tiene en el Control de Proceso Estadístico una rica colección de herramientas para monitorear un sistema. Shewhart (1926) propuso los primeros Gráficos de Control (GC), que constituyen aún, los más utilizados en los sistemas industriales de hoy.
Los GC son usados para modelar la estabilidad de los procesos. En este contexto, se dice que un proceso está en control estadístico, si la distribución de probabilidad que representa la característica de calidad es constante en el tiempo. Esta definición tradicional del SPC ha sido generalizada durante los años para incluir casos en los cuales un modelo estadístico básico de la característica de calidad es estable en el tiempo. Estas generalizaciones útiles incluyen, por ejemplo, regresión, componentes de varianza y modelos de series de tiempo.
La autocorrelación se ha reconocido desde hace mucho como fenómeno natural en las industrias de proceso. Solamente en años recientes la autocorrelación se ha convertido en salida de las aplicaciones del SPC, particularmente en las industrias de las piezas, donde el autocorrelación se ve como problema que pueda minar la interpretación de los gráficos de control. Cuando las gráficos de control se construyen con mediciones autocorrelacionadas, el resultado puede dar muchas señales falsas, haciendo que los LC se muestren demasiado apretados.
Otras evidencias son reportadas en mediciones realizadas por (Alwan y Roberts, 1995), al encontrar que más del 85% de los controles en las industrias de proceso, aplican resultados de gráficos con límites de control mal colocados. En muchos de los casos esta situación esta dada por la presencia de autocorrelaciones de los procesos observados y con violaciones en las suposiciones básicas asociadas con los gráficos de Shewhart (Woodall, 2000).
Las series de tiempo estructuradas son sucesos comunes en datos de muchas industrias de proceso, lo que complica el esfuerzo de los investigadores en calidad para la colocación correcta de los LC. En la literatura consultada en Cuba y en el resto del mundo no se tiene referencia del uso de las series de tiempo estructuradas en la industria azucarera.
Precisamente la situación problémica que llevó a la realización del presente trabajo se fundamenta en la necesidad que tiene el país de adaptarse al mercado mundial, mediante la adopción de nuevos enfoques y por las dificultades detectadas en estudios anteriores en la empresa azucarera «Melanio Hernandez», específicamente en el Tándem.
Se pretende como objetivo aplicar las series de tiempo estructuradas para evaluar la influencia de la autocorrelación en la reducción de la variabilidad en el proceso de extracción de la empresa azucarera «Melanio Hernandez», que permita explicar la variabilidad existente en este proceso.
Para el desarrollo de la investigación se tomó como objeto de estudio la empresa azucarera «Melanio Hernandez» de la Provincia de Sancti Spíritus. Y como campo de acción estudio de las variables implicadas en la variabilidad en el proceso de extracción.
Desarrollo
El entendimiento de la variación en los valores de las características de calidad es de importancia primaria en el Control de Proceso Estadístico, la «Causa común» es considerada una variación debido a la naturaleza inherente de los procesos y no puede ser alterada por un cambio externo del proceso mismo. «Causa asignable o especial» de variación son usuales choques o interrupciones, las cuales pueden ser separadas. El propósito del Control de Proceso Estadístico (SPC) es distinguir entre estos dos tipos de variación para prevenir una reacción o sobreacción.
Para características continuas de calidad, los límites de especificación son frecuentes dados en la práctica. Un artículo es considerado conforme, sí el valor de su característica de calidad está dentro de los límites de especificaciones y no es conforme, cuando está fuera.
Deming (1986) y otros autores han argumentado que encontrarse dentro de los límites de especificación no es suficiente para asegurar una buena calidad y que la variabilidad de las características de calidad tiene que ser reducida. Entonces, para muchas característica de calidad, mejoramiento de la calidad corresponde a centrar la distribución de probabilidad de la característica de calidad en un valor objetivo y reduciendo variabilidad. Taguchi (1981) insta la reducción de variabilidad hasta parecer económico y desventajoso para reducirlo más adelante.
La estimación por el modelo ARIMA de los parámetros puede no ser confiable en estos casos, si las causas asignables están presentes en los datos, además de una mala colocación de los LC si las entradas son dinámicas, exhibiendo una serie de tiempo estructurada. Las series de tiempo explican la mayoría de las variaciones en los datos al margen de independencia y la idéntica distribución de los residuales.
Si la serie es contaminada por períodos de disturbios externos para el proceso, el modelo ARIMA puede ser incorrectamente especificado, la variabilidad de los residuales es sobre estimada y los límites de control mal colocados.
Box and Tiao (1978) con el Modelo de la Función de Transferencia, describen la característica de calidad observada () como una función de tres causas de variabilidad, dadas por la siguiente ecuación:
= Entradas dinámicas + Intervención + ARIMA
Las entradas dinámicas que representan una función de impulso, aplicado para la entrada con un retardo de períodos de tiempos. Si la relación dinámica entre la entrada y la salida de la serie de tiempo existe, el valor retardado del proceso puede ser modelado, resultando una considerable reducción de la varianza no explicada.
El término de intervención identifica períodos de tiempo cuando las causas asignables están presentes en el proceso. Box, Jenkins y Reisel (1994). El término de intervención es una razón polinomial que define la naturaleza del disturbio (inestabilidad).
Modelo básico de ARIMA.
El principal objetivo que se persigue al moler la caña es extraer la mayor cantidad posible de sacarosa que ésta contiene, de ahí la importancia que reviste esta área.
Entiéndase como extracción: El total de azúcar extraído por el tándem, como por ciento del azúcar en la caña. Conforme lo define la Sociedad Internacional de Tecnólogos de la caña de azúcar, es la sacarosa en el jugo mezclado, por cada cien partes de sacarosa en la caña.
La pérdida de sacarosa por no-extracción varía entre 4 y 7 % del total de sacarosa en la caña y es por eso que el proceso de molienda debe encaminarse a obtener la mayor extracción posible del jugo contenido con el mínimo costo. Pérez de Alejo (1979), demuestra que la extracción en el Tándem es la que más afecta las ganancias en un central azucarero, siendo este criterio compartido con Riera (1996).
Para el análisis del proceso de extracción se tomaron las Características de Calidad (CC) que identifican los dos productos resultado de este proceso: Bagazo (B) y Jugo Mezclado (JM) y se estudiaron las variables Pol del bagazo, Humedad del bagazo, Brix del jugo mezclado, Pol del jugo mezclado, acidez del jugo mezclado y pureza del jugo mezclado.
Primeramente se hizo un estudio descriptivo de todas las variables tecnológicas que influyen en el proceso de extración. A continuación se muestran los resultados:
Tabla 1. Estadísticos descriptivos de las CC que identifican el B y JM.
| Parámetros \ Variables | Pol en B | Humedad del B | Brix del JM | Pol del JM | Pureza del JM | Acidez del JM |
| N | 100 | 99 | 100 | 100 | 100 | 100 |
| Media | 2,3804 | 50,7579 | 15,4366 | 13,2092 | 85,5312 | 0,5940 |
| Moda | 2,20 | 50,08 | 15,56 | 12,79 | 84,02 | 0,55 |
| DT | 0,25379 | 1,21619 | 0,69993 | 0,63007 | 1,81035 | 0,09081 |
| Asimetría (A) | 1,243 | 0,696 | -0,069 | -0,078 | -0,315 | 0,506 |
| Curtosis (C) | 1,380 | 4,490 | -0,400 | -0,788 | -0,343 | 0,441 |
| Mínimo | 1,97 | 46,17 | 13,80 | 11,82 | 79,90 | 0,38 |
| Máximo | 3,35 | 55,40 | 17,31 | 14,44 | 88,49 | 0,87 |
El tipo de GC a utilizar depende de las características del proceso y su elaboración se realiza a partir de la distribución que siguen las variables analizadas, para la selección de las constantes con la información obtenida por el SPSS. La evaluación del estado de control del proceso se realiza de forma aparente según la representación gráfica obtenida del GC y por análisis de variabilidad propuesto por Ishikawa (1992).
Los GC utilizados fueron del tipo X-Rm (valores individuales y recorridos móviles) por la sugerencia de Juran (1988), NC 92.11.80, acerca de las aplicaciones de estos gráficos, cuando no es posible formar subgrupos racionales (SGR) por las características de los datos, dada la naturaleza del proceso que es relativamente uniforme (debido al efecto de las mezclas que ocurren en el proceso de producción).
Para todas la variables analizadas (Campos, A. Y, Blanco, G. E, 2004) se manifestó un proceso fuera de control estadístico no solo por la presencia de puntos fuera de los LC, sino por observarse adherencias: al LC superior al inicio de la zafra, caracterizando la deficiente operación en este período y en el LC inferior en el período normal de operación, lo que pudiera ser resultado de la intervención del hombre para lograr valores los más cercanos a las planes por los que son evaluados y estimulados.
Al identificarse patrones no aleatorios, se require de la profundización en el estudio del proceso a través de las ST, que no pueden ser estudiadas con las técnicas básicas de regresión, porque en la mayoría de los casos, los valores de la serie están autocorrelacionadas. En los trabajos de (Gómez, 1998), al utilizar GC de medias móviles, se evidenció la presencia de autocorrelación en el proceso de extracción, al obtenerse LC muy estrechos, elemento que la literatura identifica como manifestación de este fenómeno.
La metodología de Box- Jenkins para el estudio de ST no estacionales, es utilizada en la determinación del modelo ARIMA de las variables. La evaluación se realizó con el SPSS. A modo de ejemplo se explica a continuación el tratamiento dado a la variable Pureza del jugo mezclado.
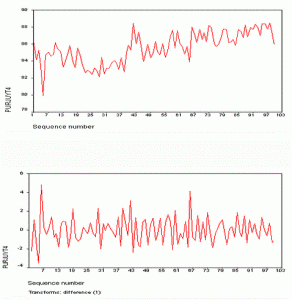
1. Ploteo de la serie. El gráfico obtenido da la posibilidad de visualizar la no estacionaridad que presenta Prueza del jugo mezclaado (PJM) y por ende la necesidad de una diferenciación de orden 1.
2. Ploteo de La Función de Autocorrelación (ACF) y las Función de Autocorrelación Parcial (PACF). Los correlogramas que se muestran en la figura 1 permiten reafirmar la estacionaridad que brindó el paso anterior, por lo que es posible pasar a la identificación del modelo que sigue cada serie.
Para ver el gráfico seleccione la opción «Descargar» del menú superior
Fig. 1. Correlogramas de las ACF y PACF de la PJM.
3. Identificación del modelo. Con el análisis de los gráficos ACF y PACF se identificaron los modelos que caracterizan las series, en el caso de la PJM el modelo seleccionado es un ARIMA (0,1,1).
4. Ploteo de residuales ACF y PACF. El ploteo de los residuales obtenidos en la figura 2 (ACF, con similar comportamiento el PACF), permite conocer si el modelo obtenido para la serie sea adecuado o no, a través del análisis de la existencia de ruidos blancos.
Para ver el gráfico seleccione la opción «Descargar» del menú superior
Fig. 2. Ploteo de los residuales ACF y PACF de la PJM.
Una vez modelada la característica de calidad PJM se hicieron los gráficos de control de los residuales que se muestran a continuación:
Para ver el gráfico seleccione la opción «Descargar» del menú superior
Fig 3. Gráficos de control de los residuales del modelo ARIMA.
La presencia de causas asignables de variación en los GC de los residuos del modelo ARIMA (figura 3), permiten evaluar la cuantía de su efecto en la variabilidad del proceso, la identificación de los momentos que tales comportamientos ocurren y la posibilidad de atenuar tales efectos con la consiguiente reducción de variabilidad. Para ello se realizó un análisis de intervención. A continuación se muestran los gráficos de control una vez realizado el análisis de las intervenciones.
Para ver el gráfico seleccione la opción «Descargar» del menú superior
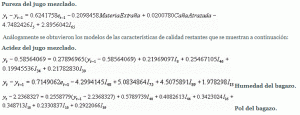
Una vez realizado el análisis de las causas asignables relacionadas con la operación del proceso, se procedió a la evaluación de las entradas al proceso, obteniedose sólo para el modelo referido a la Pureza del JM una dependencia de las materias extrañas y el porcentaje de caña atrasada.
El modelo obtenido fue el siguiente:
Los modelos obtenidos permitieron evaluar la contribución a la reducción de variabilidad del proceso de extracción como se muestra en la Tabla 3.
| Parámetros/ Variables | Acidez del Jugo mezclado | Pureza del Jugo mezclado | Humedad del bagazo | Pol del bagazo |
| Desviación del error estándar inicial | 0,08854142 | 1,2195183 | 1,1346052 | 0,1391749 |
| Desviación del error estándar final | 0,0769999 | 1,0165379 | 0,7275653 | 0,09319682 |
| Porcentaje de reducción de variabilidad | 13,04% | 16,64% | 35,86% | 33,04% |
Tabla 3.1. Resumen de la reducción de variabilidad para cada variable.
Con la utilización de las herramientas desarrolladas se concretiza el modelo que caracteriza el proceso analizado, de forma que pueda ser utilizado en el monitoreo de la calidad. Con esta modelación se tiene la desventaja de la pérdida de simplicidad de los gráficos Shewhart, pero se garantiza una mayor exactitud en el cálculo de la variabilidad del proceso y por tanto mnimizar el problema de la mala colocación de los LC y con ello una contribución al mejoramiento.
Conclusiones
Se aplicaron por primera vez en la industria azucarera cubana las series de tiempo estructuradas para evaluar la influencia de la autocorrelación en la reducción de variabilidad en el proceso de extracción de la empresa azucarera «Melanio Hernández».
Se realizaron análisis de autocorrelación que permitieron obtener los modelos que explican la variabilidad del proceso, para cuyos ajustes se identificaron causas asignables, que permiten una reducción de variabilidad en: 13,04% para la Acidez del JM; 16,64% para la Pureza del JM.; 35,84% para la Humedad del B; 33,04% para la Pol del B.
Bibliografía.
Alwan, L. C. and Roberts, H. V. (1988). Time- Series Investigation Modeling for Statistical Process Control .Journal of Business and Economic Statistical 6 , pp. 87- 95.
Alwan, L. C. and Roberts, H. V. (1995). «The Problem with Misplaced Control Limits». Applied Statistical. 44. pp. 269- 278.
Box, G. E. P., Jenkins, G. M. and Reinsel, G. C. (1994). «Time Series Analysis. Forecasting and Control. Preentice Hall. Englewood Clitls, NJ, pp 392- 478.
Burr, W. I. The Effect of Non- Normality on Constants for X and R Charts. Industrial Quality Control. May 1967. Pp 563- 568.
Campos, A. Y, Blanco, G. E. Influencia de la autocorrelaciòn en la industria azucarera. TD, CUSS. 2004
Cuba. Ministerio del azúcar. Manual de operaciones de planta moledora./ MINAZ. – La Habana, 1996. – 91p.
Gómez A, Bismayda. Mejoramiento de la calidad en procesos de la industria azucarera./ B. Gómez A; Ramón Pons Murguía, tutor,___ Tesis maestría; UCLV, 1998, ___ 80h.
Gómez A, B. et al. Desarrollo de un estudio de caso en procesos de un central azucarero, a través de un procedimiento para el mejoramiento de la calidad. Revista Centro Azúcar, No. 4, 2002. UCLV.
Gómez A, B. et al. Trabajo presentado: «Experimental Design Using a Response Surface Technique for Process». «53rd Canadian Chemical Engineering & PRES’03 Conference». Hamilton, Ontario, Canada- October 26- 29, 2003.
Grau, R. A., Conferencia de series de tiempo. UCLV, 1995.
Ishikawa, Kauro. Introduction to Quality Control. 3ra Edición, Editorial 3ª Corporation. Tokyo, Japan, 1992.
NIST. National Istitute of Standards and Technology. Statistical Engineeering Division. 7/2/2001.
Peláez, G, Mileydi. Aplicación del Control Estadístico de Proceso en el análisis de variables de preparación de la caña y extracción en seco en el central ¨Melanio Hernández./ M. Peláez; Bismayda Gómez A, tutor. – TD; UCLV, 1999, -80h.
West D. and Dellana S. «Transfer Function Modeling of Processes with Dinamic Inputs» Journal of Quality Technology. Vol. 34. No. 3 July 2002.
Woodall, H. W. Controversies and Contradictions in Statistical Process Control. Journal of Quality Technology. Vol. 32. No.4. October 2000. pp 341- 350.