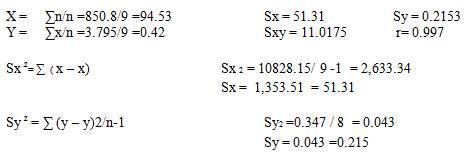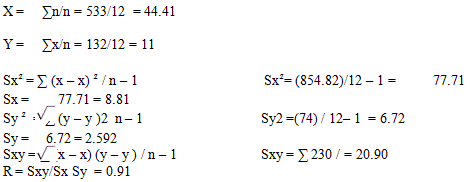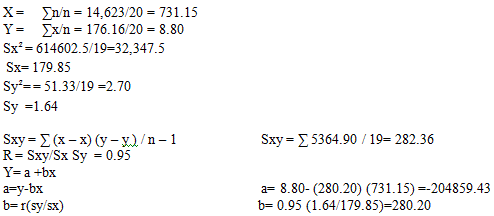1. Objetivo:
Que el alumno aprenda y analice los diagramas de dispersión en minitab para un mayor aprendizaje en el programa de minitab.
2. Antecedentes:
*Variable:
Es una característica (magnitud, vector o número) que puede ser medida, adoptando diferentes valores en cada uno de los casos de un estudio.
*Medición:
Es la determinación de la proporción entre la dimensión o suceso de un objeto y una determinada unidad de medida
*Diagrama de dispersión:
Los Diagramas de Dispersión o Gráficos de Correlación permiten estudiar la relación entre 2 variables. Dadas 2 variables X e Y, se dice que existe una correlación entre ambas si cada vez que aumenta el valor de X aumenta proporcionalmente el valor de Y (Correlación positiva) o si cada vez que aumenta el valor de X disminuye en igual proporción el valor de Y (Correlación negativa).
En un gráfico de correlación representamos cada par X, Y como un punto donde se cortan las coordenadas de X e Y.
Gráfica realizada trazando puntos en un plano coordenado de acuerdo con los valores pares observados para mostrar la relación entre dos variables.
*Coeficiente de correlación:
El coeficiente de correlación lineal es el cociente entre la covarianza y el producto de las desviaciones típicas de ambas variables.
El coeficiente de correlación lineal se expresa mediante la letra r.
*Regresión entre dos variables:
Es un método matemático que modeliza la relación entre una variable dependiente Y, las variables independientes Xi y un término aleatorio ε.
3. Ejemplos teóricos
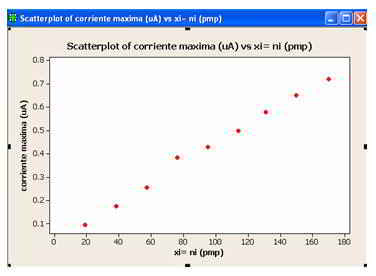
1. Por medio de un procedimiento químico llamado polarografía diferencial de pulsos un químico midió la corriente máxima que se generó (en microamperes) al agregar una solución que contenía una cantidad determinada de níquel (en partes por mil millones, pmm) a una solución amortiguadora. Los datos se presentan a continuación:
| x = Ni (pmm) | y = Corriente máxima (?A) |
| 19.1 | 0.095 |
| 38.2 | 0.174 |
| 57.3 | 0.256 |
| 76.2 | 0.384 |
| 95 | 0.429 |
| 114 | 0.500 |
| 131 | 0.580 |
| 150 | 0.651 |
| 170 | 0.722 |
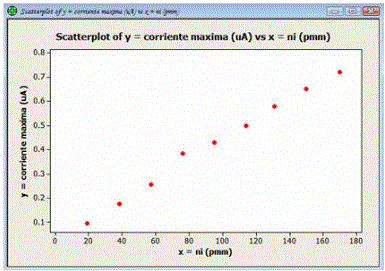
a) Elabore un diagrama de dispersión con estos datos.
b) Calcule el coeficiente de correlación, r.
(A) Calcule el coeficiente de correlación.
| X | Y | ( x ? x) | ( x ? x ) ² | ( y ? y ) | (y ? y ) ² | (x ? x ) ( y ? y ) |
| 19.1 | 0.095 | -75.43 | 5.689.68 | -0.325 | 0.10 | 24.51 |
| 38.2 | 0.174 | -56.33 | 3.173.06 | -0.246 | 0.06 | 13.85 |
| 57.3 | 0.256 | -37.23 | 1.386.07 | -0.164 | 0.02 | 06.10 |
| 76.2 | 0.384 | -18.33 | 335.98 | -0.036 | 0.00124 | 0.65 |
| 95 | 0.429 | 0.47 | 0.22 | .009 | 0.0081 | .00423 |
| 114 | 0.500 | 19.47 | 374.08 | 0.08 | 0.0064 | 1.55 |
| 131 | 0.550 | 36.47 | 1,330.06 | 0.16 | 0.02 | 5.83 |
| 150 | 0.655 | 55.47 | 3,076.92 | 0.235 | 0.05 | 13.03 |
| 170 | 0.722 | 75.47 | 5,695.72 | 0.302 | 0.09 | 22.79 |
| ? = 850.8 | ? = 3.795 | 21,066 | 0.347 | 88.61 |
———–
2. La materia prima que se usa en la elaboración de una fibra sintética se almacena en un local que no tiene control de humedad. Las mediciones de la humedad relativa en el local y del contenido de humedad de una muestra de la materia prima (ambos en porcentajes) durante 12 días, dieron los siguientes resultados:
| Humedad, X | Contenido de Humedad, Y |
| 42 | 12 |
| 35 | 8 |
| 50 | 14 |
| 43 | 9 |
| 48 | 11 |
| 62 | 16 |
| 31 | 7 |
| 36 | 9 |
| 44 | 12 |
| 39 | 10 |
| 55 | 13 |
| 48 | 11 |
Ajuste una línea recta y determine el contenido de humedad cuando la humedad del local de almacenamiento es de 40%.
| X | Y | ( x ? x) | ( x ? x )² | ( y ? y ) | (y ? y )² | (x ? x ) ( y ? y ) |
| 42 | 12 | -2.41 | 5.80 | 1 | 1 | -2.41 |
| 35 | 8 | -9.41 | 88.54 | -3 | 9 | 28.23 |
| 50 | 14 | 5.59 | 31.24 | 3 | 9 | 16.77 |
| 43 | 9 | -1.41 | 1.98 | -2 | 4 | 2.82 |
| 18 | 11 | 3.59 | 12.88 | 0 | 0 | 0 |
| 62 | 16 | 17.59 | 309.4 | 5 | 25 | 87.95 |
| 31 | 7 | -13.41 | 179.82 | -4 | 16 | 53.64 |
| 36 | 9 | -8.41 | 70.72 | -2 | 4 | 16.82 |
| 44 | 12 | 0.41 | 0.168 | 1 | 1 | -0.41 |
| 39 | 10 | -5.41 | 29.26 | -1 | 1 | 5.41 |
| 55 | 13 | 10.59 | 112.14 | 2 | 4 | 21.18 |
| 48 | 11 | 3.59 | 12.88 | 0 | 0 | 0 |
| ? =533 | ? =132 | ? =854.82 | ? =74 | ? =230 |
———–
3. Los estadounidenses conscientes de la salud consultan a menudo la información relacionada con los nutrientes que aparecen en los envases de los alimentos con el fin de evitar los que contengan grandes cantidades de grasa, sodio o colesterol. La siguiente información se tomó de ocho marcas distintas de queso americano en rebanadas:
| Marca | Grasa (g) | GrasasSaturadas (g) | Colesterol(mg) | Sodio (mg) | Calorías |
| Kraft Deluxe American | 7 | 4.5 | 20 | 340 | 80 |
| Kraft Velveeta Slices | 5 | 3.5 | 15 | 300 | 70 |
| Private Selection | 8 | 5.0 | 25 | 520 | 100 |
| Ralphs Singles | 4 | 2.5 | 15 | 340 | 60 |
| Kraft 2% Milk Singles | 3 | 2.0 | 10 | 320 | 50 |
| Kraft Singles American | 5 | 3.5 | 15 | 290 | 70 |
| Borden Singles | 5 | 3.0 | 15 | 260 | 60 |
| Lake to Lake American | 5 | 3.5 | 15 | 330 | 70 |
a) ¿Qué pares de variables espera usted que estén fuertemente relacionadas?
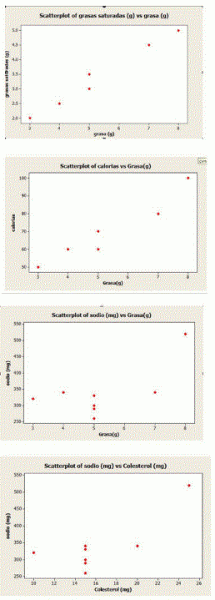
b) Trace un diagrama de dispersión para la grasa y la grasa saturada. Describa la relación.
c) Elabore un diagrama de dispersión para grasas y calorías. Compare el patrón con el observado en el inciso
d) Trace un diagrama de dispersión para la grasa y el sodio, y otro para colesterol y sodio.
e) Calcule el coeficiente de correlación r para las variables de colesterol y sodio
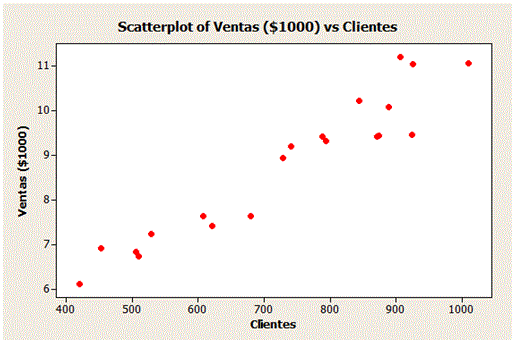
4. Suponga que el gerente de una cadena de servicios de entrega de paquetería desea desarrollar un modelo para predecir las ventas semanales (en miles de dólares) para las tiendas individuales basado en el número de clientes que realizan las compras. Se seleccionó una muestra aleatoria entre todas las tiendas de la cadena con los siguientes resultados:
| Tienda | Clientes | Ventas ($1000) |
| 1 | 907 | 11.20 |
| 2 | 926 | 11.05 |
| 3 | 506 | 6.84 |
| 4 | 741 | 9.21 |
| 5 | 789 | 9.42 |
| 6 | 889 | 10.08 |
| 7 | 874 | 9.45 |
| 8 | 510 | 6.73 |
| 9 | 529 | 7.24 |
| 10 | 420 | 6.12 |
| 11 | 679 | 7.63 |
| 12 | 872 | 9.43 |
| 13 | 924 | 9.46 |
| 14 | 607 | 7.64 |
| 15 | 452 | 6.92 |
| 16 | 729 | 8.95 |
| 17 | 794 | 9.33 |
| 18 | 844 | 10.23 |
| 19 | 1010 | 11.77 |
| 20 | 621 | 7.41 |
a) Grafique el diagrama de dispersión.
b) Obtenga la ecuación que mejor ajuste a los datos.
c) Pronostique las ventas semanales (en miles de dólares) para las tiendas que tienen 600 clientes.
| X | Y | ( x ? x) | ( x ? x ) ² | ( y ? y ) | (y ? y ) ² | (x ? x ) ( y ? y ) |
| 907 | 11.20 | 175.85 | 30923.22 | 2.4 | 5.76 | 422.04 |
| 925 | 11.05 | 194.85 | 37966.52 | 2.25 | 5.06 | 438.91 |
| 506 | 6.84 | -225.15 | 50692.52 | -1.96 | 3.84 | 441.2 |
| 741 | 9.21 | 9.85 | 97.02 | 0.41 | 0.16 | 4.03 |
| 789 | 9.42 | 57.85 | 3346.62 | 0.62 | 0.38 | 35.98 |
| 889 | 10.08 | 157.85 | 24916.61 | 1.28 | 1.63 | 202.09 |
| 874 | 9.45 | 142.85 | 20406.12 | 0.64 | 0.41 | 91.85 |
| 510 | 6.73 | -221.15 | 48907.32 | -2.07 | 4.31 | 457.70 |
| 529 | 7.24 | -202.15 | 40864.62 | -1.56 | 2.45 | 315.35 |
| 420 | 6.12 | -311.15 | 96814.32 | -2.68 | 7.22 | 833.88 |
| 679 | 7.63 | -52.15 | 2719.62 | -1.17 | 1.38 | 61.01 |
| 872 | 9.43 | 140.85 | 19838.72 | 0.63 | 0.386 | 88.73 |
| 924 | 9.46 | 192.85 | 37119.12 | 0.66 | 0.425 | 127.28 |
| 607 | 7.64 | -124.15 | 15413.22 | -1.16 | 1.364 | 144.01 |
| 452 | 6.92 | -279.15 | 77924.72 | -1.88 | 3.564 | 527.70 |
| 729 | 8.95 | -2.15 | 4.62 | 0.15 | 0.02 | -0.215 |
| 794 | 9.33 | 62.85 | 3950.12 | 0.53 | 0.272 | 33.31 |
| 844 | 10.23 | 112.85 | 12735.12 | 1.43 | 2.02 | 161.37 |
| 1010 | 11.77 | 278.85 | 77757.32 | 2.97 | 8.77 | 828.18 |
| 621 | 7.41 | -110.15 | 12133.02 | -1.39 | 1.95 | 153.10 |
| ? =14,623 | ? =176.16 | 61460.25 | 51.33 | 5364.90 |
Por tanto, la recta de mejor ajuste es Y= -204859.43+280.20 X
4. Manual de usuario para el uso de minitab.
1) Primero seleccionamos el icono de minitab, y hacemos click en botón derecho
2 ) Después aparecerá el programa, ya abierto
3) Le añades los datos que vas a utilizar
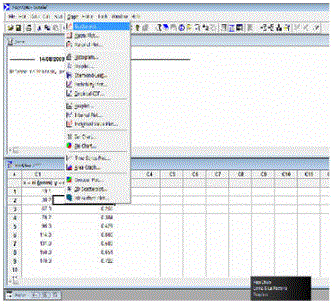
4 ) Seleccionas el icono Graph , después la opcion scatterplot.
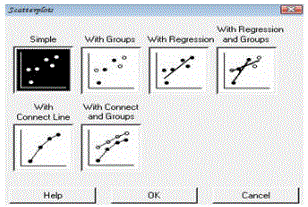
5) Aparecerá el siguiente cuadro, en el cual deberas pulsar el icono Ok
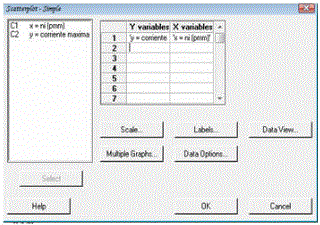
6) Agregas las variables a las columnas, que aparecen y pulsas Ok
7) Aparecerá realizado el diagrama de dispersión
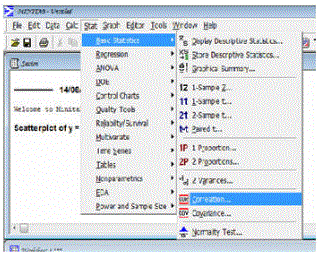
8.) Para realizar el coeficiente de correlación seleccionas el icono Stat con la opción Basic Statistics con la opción correlación
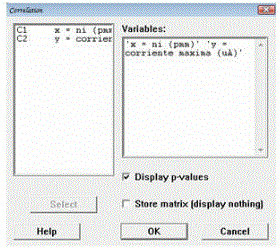
9 ) Agregas las variables a la columna derecha, y le das click a Ok
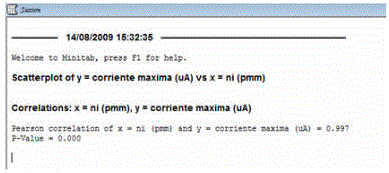
10) Por último, te da el resultado de la correlación
5. Conclusiones:
El trabajo de realizar problemas guiados por el programa de minitab ya que en este programa es más fácil realizar todos los problemas.
6. Experiencia y aprendizaje:
Con este proyecto nosotros aprendimos a usar el magnificó programa de minitab ya que en este programa se resuelven las cosas muy fácilmente porque en el podemos realizar las graficas, etc… Y este programa nos servirá en un futuro, queremos agradecer al ingeniero Luis Arturo García Navarro, por encargarnos este proyecto.
7. Bibliografía: http//: Wikipedia y monografías