Unidad didáctica para la enseñanza de trinomios

Autor: Wilcar Damian Cifuentes Álvarez

Matemáticas financieras

03-2007

La historia del algebra se remonta al antiguo Egipto y Babilonia, donde fueron capaces de plantear y resolver problemas que contenían ecuaciones de primer y segundo grado. Los antiguos babilonios resolvieron ecuaciones, utilizando en esencia los mismos métodos que utilizamos hoy.

PLANTEAMIENTO DEL PROBLEMA

En los procesos de enseñanza y de aprendizaje muy a menudo nos encontramos con muchos factores determinantes en la construcción del conocimiento, uno de ellos es el poco interés o amor hacia el estudio hacia las matemáticas, provocando preocupaciones en la educación básica secundaria, más precisamente en el Colegio Manuel German Cuello Gutiérrez en la jornada de la tarde, en donde la observación a los procesos de aprendizaje evidencian que los alumnos no logran un aprendizaje significativo del algebra, específicamente en la factorización de trinomios.

Es deber de los docentes proponer alternativas que posibiliten el mejoramiento de los procesos de enseñanza y de aprendizaje que lleven al estudiante a despertar el interés por las matemáticas y apropiarse del conocimiento, ayudando al desarrollo de la memoria semántica, que conllevará al fortalecimiento de los conocimientos previos, convirtiéndolos en un aprendizaje significativo.

Toda lo anterior, lleva al siguiente interrogante:

Permitirá la elaboración de un software, como estrategia metodológica innovativa lograr un aprendizaje significativo de la factorización de trinomios?

OBJETIVOS

OBJETIVO GENERAL

· Diseñar y validar estrategias metodológicas innovativas que permitan un aprendizaje significativo del concepto de las expresiones algebraicas en la descomposición de trinomios.

OBJETIVOS ESPECIFICOS

Ø Aplicar actividades pedagógicas relacionadas con la solución de problemas sobre expresiones algebraicas y la descomposición de ellas en sus factores primos.

Ø Mejorar las relaciones interpersonales entre alumno-alumno y alumno-profesor.

Ø Disminuir la apatía de los alumnos hacia el estudio de las matemáticas.

JUSTIFICACION

La constitución política de Colombia de 1991 en el artículo 67 expresa que “La educación es un derecho de la persona y un servicio público que tiene una función social: con ella se busca el acceso al conocimiento, a la ciencia y la técnica y a los demás bienes y valores de la cultura”. En el mismo sentido, la Ley general de Educación en su articulo 1 enuncia que “La educación es un proceso de formación permanente, cultural y social que se fundamenta en una concepción integral de la persona humana, de su dignidad, de sus derechos y sus deberes”; lo que indica que el docentes es un permanente constructor del conocimiento y está en la obligación de establecer estrategias innovadoras que ayuden a mejorar la calidad de la educación.

El aprendizaje como un proceso natural, social, activo y no pasivo, puede ser lineal o no lineal; además, es integrado y contextualizado, basado en un modelo que debe ser cambiante; se fortalece en contacto con las habilidades, interés y cultura del estudiante. Este aprendizaje natural debe ser acompañado por el docente, a quien le corresponde ser un agente activo en el proceso y no la maquina que lo sabe todo; por el contrario, debe ir aprendiendo con sus alumnos.

Habitualmente, en la enseñanza de las matemáticas dominaba el modelo transmisivo-receptivo, donde el profesor elabora contenidos que el alumno recibe pasivamente. Este modelo didáctico, que adopta la clase magistral como prototipo, transmite una visión de las matemáticas muy ortodoxa, con saberes ya hechos, donde los contenidos son netamente memorísticos. Algunas investigaciones sobre la visión y la actitud que adquieren los alumnos ante el estudio de las matemáticas, a lo largo de su vida educativa en el colegio, revelan una situación preocupante. Los estudios más interesados en el aprendizaje de las matemáticas, reflejan una creciente apatía de los jóvenes frente a las matemáticas. El panorama se agravaba al comprobar que esos mismos jóvenes habían iniciado los primeros contactos con la ciencia desde la curiosidad y hasta el entusiasmo, o sea de la manipulación directa de los contenidos teóricos. De alguna manera parece suceder que la propia enseñanza de las matemáticas aleja a una parte importante de los niños de sus intereses iniciales por el conocimiento.

La enseñanza de las matemáticas, bajo el modelo tradicional de recepción de conocimientos elaborados, pone toda su preocupación en los contenidos, de forma que sobresale una visión despreocupada del propio proceso de enseñanza, entendiéndose que enseñar constituye una tarea sencilla que no requiere especial preparación. Esta concepción ha pesado sobre las propias formaciones iniciales que exige a los profesores de matemáticas, de forma que las demandas se reducen al propio conocimiento de las materias y contenidos a impartir, y muy poco o nada a las cuestiones didácticas o de cómo enseñar.

Estos métodos de enseñanza prosperaron hasta fines del siglo XX, cuando aparece la pedagogía y uno de sus precursores: Erasmo de Rótterdam, rompe con la antigua forma de educar, cuyo aspecto esterilizante y repetitivo había sido ampliamente denunciado. Es el primero que destaca el valor de la afectividad y del juego en el aprendizaje del conocimiento. Con esta reflexión, Juan Amos Comenio presenta una nueva metodología de la educación, basada en la unión de la pedagogía con la didáctica, su proyecto de una “didáctica magna” o “instrucción universal” inspirada en principios religiosos y humanistas, ayuda al maestro a diseñar estrategias que le permiten al estudiantes a asimilar los conocimientos de manera fácil. Aún así, existen algunos baches difíciles de solucionar, es aquí donde entra a jugar un papel muy importante la psicología de la educación, que es la aplicación del método científico al estudio del comportamiento de los individuos y grupos sociales en los ambientes educativos.

La psicología de la educación no sólo se ocupa de la conducta de profesores y estudiantes, sino que también se aplica a otros grupos como los ayudantes de los profesores, primera infancia, inmigrantes y tercera edad. Las áreas de estudio de la psicología de la educación se superponen inevitablemente con otras áreas de la psicología, incluyendo la psicología del desarrollo (del niño y del adolescente).

Por todo lo anterior, los docentes tienen la obligación de buscar estrategias que lleven al estudiante a utilizar la memoria semántica para la solución de problemas, logrando un aprendizaje significativo.

MARCO TEORICO

Así como la aritmética surgió de la necesidad que tenían los pueblos primitivos de medir y contar; el origen del algebra es muy posterior, puesto que debieron transcurrir muchos siglos para que el hombre llegara al concepto abstracto de número, fundamento del Algebra. El gran desarrollo experimentado por el Algebra se debió sobre todo a los matemáticos árabes. Los árabes introdujeron en occidente la numeración y el Algebra, recogiendo la herencia científica de los griegos, asimilando el espíritu práctico de las matemáticas de la India y perfeccionando el sistema de numeración posicional. La palabra álgebra proviene de Ilm al-jabr w’ al mugabala (“ciencia de la restauración y la reducción”), nombre de un libro escrito en el siglo IX por el matemático árabe Al-Khwarizmi. Algunos expertos definen al álgebra como una generalización de las matemáticas gracias a la utilización de símbolos o letras para la representación números arbitrarios.

El tema de resolver ecuaciones algebraicas ha interesado a matemáticos de todos los tiempos, incluidas las antiguas civilizaciones de Babilonia y Egipto. Existen evidencias de que los egipcios resolvieron ciertas ecuaciones cuadráticas 2.000 años a.C., los Hindúes y los árabes lograron algunos avances importantes en éste tema alrededor del año 800 a.C.; pero los primeros pasos hacia el desarrollo de la teoría de ecuaciones fueron dados por Diophantus de Alejandría hacia el siglo III a. C.

Muchos son los aportes que al Álgebra han realizado innumerables matemáticos. Newton, el más grande de los matemáticos ingleses y uno de los mayores científicos de la historia de la humanidad; realizó grandes aportes, entre ellos se encuentra el binomio que lleva su nombre y el método de aproximaciones sucesivas para encontrar las cuencas de atracción. El francés Francois Viete, considerado por muchos como el fundador del Álgebra moderna, introdujo la notación algebraica, consiguiendo que el Álgebra se liberara definitivamente de las limitaciones impuestas por la aritmética, y se convirtiera en una ciencia puramente simbólica; resolvió ecuaciones de sexto grado, autor de “Isagoge in artem analyticum”, considerado como el primer tratado de álgebra.

Paolo Ruffini; además de la regla que lleva su nombre para dividir un polinomio en x, por x - a, fuel primero en hacer un intento serio de demostrar la imposibilidad de la resolución de ecuaciones polinómicas de grado superior al cuarto mediante radicales, conocido como el teorema de Abel-Ruffini; cuya formulación y demostración fue completada por el noruego Hiels Henrik Abel.

Joseph Luís Lagrange, trabajó “sobre la resolución de ecuaciones numéricas”; Karl Friederich Gauss, demostró el teorema fundamental del álgebra y Fermat, trabajó sobre la factorización y conjeturó que los números de la forma 22n+1 eran primos, conocidos hoy día como números de Fermat, quien realizó investigaciones sobre las propiedades de los números, que nunca quiso publicar; incluso, llegó a escribirle a su amigo Pascal: "No quiero que aparezca mi nombre en ninguno de los trabajos considerados dignos de exposición pública". Contribuyó a la teoría de la probabilidad, al cálculo y a la teoría de números. Una de sus contribuciones más importante fue hallar la segunda pareja de números amigos. “Dos números naturales n y m son amigos si la suma de de los divisores de es igual a m y la suma de de los divisores de m es igual a n”. Los pitagóricos descubren la primera pareja: 220 y 284. Fermat, descubre la segunda: 17296 y 18416.

FACTORIZACIÓN

1. TRINOMIO CUADRADO PERFECTO

Una cantidad es cuadrado perfecto, cuando es el cuadrado de otra cantidad; es decir, cuando es el producto de dos factores iguales. Un trinomio ordenado con respecto a una variable es cuadrado perfecto cuando el primer y el tercer término son cuadrados perfectos y el segundo término es el doble producto de sus raíces cuadradas. Para factorizar un trinomio cuadrado perfecto se extrae la raíz cuadrada al primer y el tercer término del trinomio y se separan estas raíces por el signo del segundo término. El binomio así formado, que es la raíz cuadrada del trinomio, se multiplica por si mismo o se eleva al cuadrado.
Ejemplo: factorizar x² + 2x + 1.
La raíz de x² es x; y la raíz de 1, es 1

Así:

2. TRINOMIO CUADRADO DE LA FORMA: x² + bx + c

Este trinomio cumple con las siguientes características: el primer término debe tener raíz cuadrada exacta, la variable que acompaña el segundo término debe ser la raíz cuadrada del primer término.
Para factorizar un trinomio de esta forma se debe organizar el trinomio en forma decreciente y se escribe como el producto de dos binomios, tal que los dos segundos términos de los binomios den como producto el tercer término del trinomio y su suma, el coeficiente del segundo; es decir:
x² + bx + c = (x + M)(x + m), donde: M + n = b; Mn = c
Ejemplo: factorizar x² + 5x + 6
Por lo tanto: x² + 5x + 6 = (x + 2)(x + 3)

3. TRINOMIO CUADRADO DE LA FORMA ax² + bx + c

Este trinomio debe cumplir con las siguientes características: estar organizado en forma decreciente, primer término tiene coeficiente diferente de 1 y la parte literal debe tener raíz cuadrada exacta, la variable en el segundo término debe ser la raíz cuadrada de la variable del primer término

Para factorizar el trinomio ax² + bx + c, se procede de la siguiente forma: se multiplica y divide el trinomio por el coeficiente del primer término, quedando así: de la siguiente forma: a(ax² + bx + c.)/a, luego se opera, dando como resultado: [(ax)² + b(ax) + ac)] /a; el trinomio obtenido es un trinomio de la forma x² + bx + c.

APRENDIZAJE SIGNIFICATIVO.

Un aprendizaje es significativo cuando los contenidos: Son relacionados de modo no arbitrario y sustancial (no al pie de la letra) con lo que el alumno ya sabe. Por relación sustancial y no arbitraria se debe entender que las ideas se relacionan con algún aspecto existente específicamente relevante de la estructura cognoscitiva del alumno, como una imagen, un símbolo ya significativo, un concepto o una proposición (AUSUBEL; 1983, 18). Esto quiere decir que en el proceso educativo, es importante considerar lo que el individuo ya sabe (ideas previas) de tal manera que establezca una relación con aquello que debe aprender. Este proceso tiene lugar si el educando tiene en su estructura cognitiva conceptos, estos son: ideas, proposiciones, estables y definidos, con los cuales la nueva información puede interactuar.

El aprendizaje significativo ocurre cuando una nueva información "se conecta" con un concepto relevante preexistente en la estructura cognitiva, esto implica que, las nuevas ideas, conceptos y proposiciones pueden ser aprendidos significativamente en la medida en que otras ideas, conceptos o proposiciones relevantes estén adecuadamente claras y disponibles en la estructura cognitiva del individuo y que funcionen como un punto de "anclaje" a las primeras.

TIPOS DE APRENDIZAJE SIGNIFICATIVO

Es importante recalcar que el aprendizaje significativo no es la "simple conexión" de la información nueva con la ya existente en la estructura cognoscitiva del que aprende; por el contrario, sólo el aprendizaje mecánico es la "simple conexión", arbitraria y no sustantiva; el aprendizaje significativo involucra la modificación y evolución de la nueva información, así como de la estructura cognoscitiva envuelta en el aprendizaje.

Ausubel distingue tres tipos de aprendizaje significativo: de representaciones conceptos y de proposiciones.

1 Aprendizaje De Representaciones
Es el aprendizaje más elemental del cual dependen los demás tipos de aprendizaje. Consiste en la atribución de significados a determinados símbolos, al respecto AUSUBEL dice:
Ocurre cuando se igualan en significado símbolos arbitrarios con sus referentes (objetos, eventos, conceptos) y significan para el alumno cualquier significado al que sus referentes aludan (AUSUBEL;1983, 46).

Este tipo de aprendizaje se presenta generalmente en los niños, por ejemplo, el aprendizaje de la palabra "Pelota", ocurre cuando el significado de esa palabra pasa a representar, o se convierte en equivalente para la pelota que el niño está percibiendo en ese momento, por consiguiente, significan la misma cosa para él; no se trata de una simple asociación entre el símbolo y el objeto sino que el niño los relaciona de manera relativamente sustantiva y no arbitraria, como una equivalencia representacional con los contenidos relevantes existentes en su estructura cognitiva.

2 Aprendizaje De Conceptos

Los conceptos se definen como "objetos, eventos, situaciones o propiedades de que posee atributos de criterios comunes y que se designan mediante algún símbolo o signos" (AUSUBEL 1983:61), partiendo de ello podemos afirmar que en cierta forma también es un aprendizaje de representaciones.

Los conceptos son adquiridos a través de dos procesos. Formación y asimilación. En la formación de conceptos, los atributos de criterio (características) del concepto se adquieren a través de la experiencia directa, en sucesivas etapas de formulación y prueba de hipótesis, del ejemplo anterior podemos decir que el niño adquiere el significado genérico de la palabra "pelota" , ese símbolo sirve también como significante para el concepto cultural "pelota", en este caso se establece una equivalencia entre el símbolo y sus atributos de criterios comunes. De allí que los niños aprendan el concepto de "pelota" a través de varios encuentros con su pelota y las de otros niños.

El aprendizaje de conceptos por asimilación se produce a medida que el niño amplía su vocabulario, pues los atributos de criterio de los conceptos se pueden definir usando las combinaciones disponibles en la estructura cognitiva por ello el niño podrá distinguir distintos colores, tamaños y afirmar que se trata de una "Pelota", cuando vea otras en cualquier momento.

3 Aprendizaje de proposiciones.

Este tipo de aprendizaje va más allá de la simple asimilación de lo que representan las palabras, combinadas o aisladas, puesto que exige captar el significado de las ideas expresadas en forma de proposiciones.

El aprendizaje de proposiciones implica la combinación y relación de varias palabras cada una de las cuales constituye un referente unitario, luego estas se combinan de tal forma que la idea resultante es más que la simple suma de los significados de las palabras componentes individuales, produciendo un nuevo significado que es asimilado a la estructura cognoscitiva. Es decir, que una proposición potencialmente significativa, expresada verbalmente, como una declaración que posee significado denotativo (las características evocadas al oír los conceptos) y connotativo (la carga emotiva, actitudinal e ideosincrática provocada por los conceptos) de los conceptos involucrados, interactúa con las ideas relevantes ya establecidas en la estructura cognoscitiva y, de esa interacción, surgen los significados de la nueva proposición.

MEMORIA SEMANTICA

La memoria semántica se refiere a nuestro archivo general de conocimiento conceptual y fáctico, no relacionado con ninguna memoria en particular. Es un sistema eminentemente declarativo y explícito, pero claramente distinto del de la memoria episódica, porque de hecho se puede perder memoria de acontecimientos y mantener la memoria de conceptos. La memoria semántica muestra nuestro conocimiento del mundo, los nombres de las personas y de las cosas y su significado. Viene a estar localizada más especialmente en los lóbulos temporales ínfero laterales. Pero en un amplio sentido, la memoria semántica puede residir en las múltiples y diversas áreas de la corteza relacionadas con los diversos tipos de conocimiento. De nuevo los lóbulos frontales intervienen en su activación para recuperar la información.

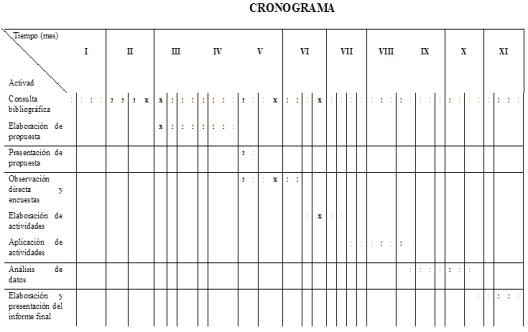
PROCESOS METODOLOGICOS

La metodología a utilizar en un una primera etapa es la observación directa, mediante la cual se llevarán los registros de los alumnos y del profesor de algebra, con el fin de establecer posibles problemas que se estén presentando en los procesos de enseñanza y aprendizaje del algebra; se realizarán entrevistas, para establecer falencias en los procesos de aprendizaje y enseñanza que no fueron observadas en la anterior etapa, en la segunda etapa se pondrán en marcha las actividades correspondientes al UNIDAD DIDACTICA PARA LA ENSEÑANZA DE TRINOMIOS, al finalizar las actividades se realizara una evaluación del proceso con los diferentes componentes que participaron del proceso.

LINEAS DE INVESTIGACION

La investigación esta enmarcada en las líneas: calidad en la enseñanza y aprendizaje de las matemáticas porque el docente de matemática esta obligado a buscar el mejoramiento de los métodos de enseñanza y aprendizaje.

POBLACIÓN

La población objeto de estudio son los estudiantes de octavo grado de la jornada de la tarde del Colegio Manuel German Cuello Gutiérrez, sus edades oscilan entre los 13 y 16 años, pertenecen a los estratos 1 y 2.

DELIMITACIÓN GEOGRAFICA

La investigación se desarrollo en el Colegio Manuel German Cuello Gutiérrez en su jornada de la tarde, ubicado en el barrio Santa Rita, al sur de la ciudad de Valledupar.

PRESUPUESTO

FOTCOPIAS……………………………….. $ 150.000
COMPRA DE LIBROS……………………..$ 250.000
TRANSPORTE…………………………….. $ 190.000
ASESORES………………………………… $1.200.000
IMPRESIONES ……………………………$ 100.000
OTROS…………………………………….. $ 300.000
TOTAL………………………………………$2.190.000

BIBLIOGRAFÍA

Aja, J. M. y otros (2000). Enciclopedia general de la educación. Tomo 2 España: Océano.
Alexis Rodríguez Gómez. (2004) Enseñanza de la matemática en Venezuela: ¿Un cuento de mendigo? Boletín Vol. II, Nº 2, Año 1995
AUSUBEL-NOVAK-HANESIAN. Psicología Educativa: Un punto de vista cognoscitivo. Editorial TRILLAS 2º ED. México. 1983.
BARON, Robert. Psicología. Editorial Prentice – Hall Hispanoamericana. México. 1996.
COLL-PALACIOS-MARCHESI. Desarrollo Psicológico y Educación II. Editorial Alianza. Madrid. 1992.
ENCICLOPEDIA DIDÁCTICA DE LAS MATEMÁTICAS. Editorial Océano. Barcelona España. 1998.
Enciclopedia Temática Lúmina siglo XXI. (2000). Matemáticas Informática. Editorial Norma. Colombia
GALDOS L. Consultor matemático (algebra). Editorial cultural s.a. Madrid España. 2003.
GOBRAN, Alfonso. Algebra elemental. Editorial grupo editorial Iberoamericano. Colombia 1990.
GUZMÁN, M. (2005). Enseñanza de las Ciencias y la Matemática. Organización de Estados Iberoamericanos para la Educación, la Ciencia y la Cultura.
HERRERA, Fernando. Introducción a la psicología. Editorial Pearson Educación. 1º ED. México. 1995.
HOFMANN, Joseph Ehrenfried. Historia de la matemática. Editorial limusa s.a. México 2002.
MÉNDEZ R. (2001) Qué es el aprendizaje significativo y en qué se diferencia del aprendizaje memorístico.
MOREIRA, M. A Teoría da Aprendizagem Significativa de David Ausubel. Fascículos de CIEF Universidad de Río Grande do Sul Sao Paulo. 1993.
NOVAK, J - GOWIN, B. Aprendiendo a Aprender. Editorial Martínez Roca. Barcelona. 1988.
PEREZ O, Edgar; PALACIO S., Emiliano y VILLAMIZAR, Armando Matemática Mega. Editorial Terranova. Bogota. 2000.
Psicología Educativa: Un punto de vista cognoscitivo .2° ED. TRILLAS México
PUENTE, Anibal. "Memoria Semántica. Teorías y Modelos". En: Psicología Cognoscitiva. Editorial Mc. Graw Hill. Caracas. 1995.
RUMELHART, David. "Hacia una comprensión de la comprensión". En la Lectura. Emma Rodríguez y Elizabeth Lager. Editorial Universidad del Valle. Cali. (1997).
WOOLFOLK, Anita. Psicología Educativa. Editorial Prentice Hall. México. 1996.