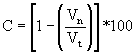Resumen
El trabajo tiene como finalidad ofrecer una metodología para la aplicación del método Delphi en las investigaciones pedagógicas.
El autor parte del análisis bibliográfico en relación con este tema y lo argumenta con un ejemplo práctico llevado a cabo en la tesis de maestría del propio investigador, lo que posibilita una mejor comprensión de las ideas expuestas.
Además, está concebido dentro de un conjunto de temas afines al respecto, que conformarán un libro electrónico acerca de la estadística aplicada a la investigación científico-pedagógica.
Mediante el empleo de hipervínculos, el trabajo articula su solución con el tabulador electrónico Excel del Windows.
Summary
The work has as purpose to offer a methodology for the application of the method Delphi in the pedagogic investigations.
The author leaves of the bibliographical analysis in connection with this topic and he argues him with a practical example carried out in the master thesis of the own investigator, what facilitates a better understanding of the exposed ideas.
In addition, it is conceived inside a group of topics tune in this respect that will conform an electronic book about the statistic applied to the scientific-pedagogic investigation.
By means of the hyperlinks employment, the work articulates its solution with the electronic tabulator Excel of the Windows.
Introducción
Muchas veces, al revisar diferentes tesis de grado científico, académico, y trabajos de diplomas, se ha observado que en algunos se hace alusión al llamado Método Delphi; pero cuando se analiza el trabajo se observa, en ocasiones, imprecisiones: en la forma de aplicar dicho método, la manera en que en se seleccionaron los expertos, y hasta en basar el análisis solamente en una ronda de consulta.
Es por ello que este trabajo tiene como objetivo aclarar todas las dudas que puedan surgir en nuestros profesores e investigadores en relación con el tema tratado, mediante la aplicación de un ejemplo práctico, tomado de la tesis de maestría del autor en la que aplica dicho método.
Antes de desarrollar el tema, se aclara que estos artículos conforman un libro electrónico del autor, por lo que existen hipervínculos que enlazan contenidos presentados en otros temas y que puedan resultar de interés su consulta. Para ello el interesado sólo debe situarse sobre él hipervínculo dado y hacer doble click.
1. ¿Qué es el método Delphi?
El método Delphi[1] consiste en la utilización sistemática del juicio intuitivo de un grupo de expertos para obtener un consenso de opiniones informadas (Valdés, 1999), (Moráguez, 2001). Resulta imprescindible que estas opiniones no se encuentren permeadas o influenciadas por criterios de algunos expertos.
Este método resulta más efectivo si se garantizan: el anonimato, la retroalimentación controlada y la respuesta estadística de grupo.
El método puede ser aplicado:
- Como previsión del comportamiento de variables conocidas; es decir, para evaluar el comportamiento de una variable conocida y así se pueda inferir posibles formas de comportamiento.
- En la determinación perspectiva de la composición de un sistema, Vg.: en el caso que los elementos del sistema a estudiar no sean conocidos, o nunca hayan sido aplicados al objeto de estudio y se orienta la muestra a la determinación de la estructura posible del sistema o modelo a aplicar.
Este último caso constituye el ejemplo que ilustramos.
2. ¿Qué ventajas tiene el método delphi?
Este autor considera, al igual de Zayas (1998), Campistrous (1998), Valdés (1999), Moráguez (2001), que las ventajas del método están dadas en que:
- Permite la formación de un criterio con mayor grado de objetividad.
- El consenso logrado sobre la base de los criterios es muy confiable.
- La tarea de decisiones, sobre la base de los criterios de expertos, obtenido por éste tiene altas probabilidades de ser eficiente.
- Permite valorar alternativas de decisión.
- Evita conflictos entre expertos al ser anónimo, (lo que constituye un requisito imprescindible para garantizar el éxito del método) y crea un clima favorable a la creatividad.
- El experto se siente involucrado plenamente en la solución del problema y facilita su implantación. De ello es importante el principio de voluntariedad del experto en participar en la investigación.
- Garantiza libertad de opiniones (por ser anónimo y confidencial). Ningún experto debe conocer que a su igual se le está solicitando opiniones.
3. ¿Cuáles son las desventajas del método delphi?
Sus desventajas más significativas están dadas en que:
- Es muy laborioso y demanda tiempo su aplicación, debido a que se requiere como mínimo de dos vueltas para obtener el consenso necesario.
- Es costoso en comparación con otros, ya que requiere del empleo de: tiempo de los expertos, hojas, impresoras, teléfono, correo…
- Precisa de buenas comunicaciones para economizar tiempo de búsqueda y recepción de respuestas.
- Debe ser llevado a cabo por un grupo de análisis: los expertos como tales.
- Se emiten criterios subjetivos, por lo que el proceso puede estar cargado de subjetividad, sometido a influencias externas.
De aquí la necesidad de aplicar varias vueltas, buscar técnicas variadas de análisis para obtener un consenso y pruebas estadísticas para determinar su grado de confiabilidad y pertinencia.
4. ¿Cómo se seleccionan los expertos y qué instrumentos se aplican?
Para la aplicación práctica del método es necesario considerar metodológicamente dos aspectos fundamentales: selección del grupo de expertos a encuestar y la elaboración del cuestionario o los cuestionarios. Pero ante todo: ¿A quiénes se pueden considerar expertos?
Se define como experto el individuo en sí, grupo de personas u organizaciones capaces de ofrecer valoraciones conclusivas de un problema en cuestión y hacer recomendaciones respecto a sus momentos fundamentales con un máximo de competencia (Valdés, 1999) (Moráguez, 2001).
De esta definición se infiere, como requisito básico para la selección de un experto, que éste tenga experiencia en el tema a consultar, dado por sus años de trabajo (praxis), y que puedan ser complementados con: conocimientos teóricos adquiridos a través de las distintas formas de superación, y grado académico o científico alcanzado en relación al tema, entre otros.
5. ¿Cómo se desarrolla el método delphi?
La explicación se basará en la forma que el autor lo realizó en su tesis de maestría (puede consultarse en la biblioteca).
Se confeccionó una “bolsa de posibles expertos” o relación de éstos, en función de las características siguientes: experiencia, competencia, creatividad, disposición a participar en la encuesta, capacidad de análisis y de pensamiento, interés colectivista y autocrítico.
Al tener en cuenta las características anteriores, se aplicó el instrumento 1, que solo fue utilizado con los posibles expertos (Anexo 1).
Así se consideró una población de 50 probables candidatos de todo el país, por estimación del autor y consultas a otros factibles expertos, de quiénes ellos consideraron pudieran ser (la decisión de hacerlo o no se mantuvo en anonimato con estos posibles expertos).
Al determinar el coeficiente de competencia se obtuvieron 30 personas que integraron la bolsa de expertos a considerar en esta temática a partir del coeficiente de competencia (K), en la que:
El coeficiente de competencia (K) del experto se determina como:
- Kc: coeficiente de conocimiento sobre el tema que se le pide opinión. Este coeficiente se autovalora acorde con el valor de la escala (Anexo 1, pregunta 1). Este valor, propuesto por el posible experto, se multiplica por 0,1 y se obtiene una puntuación, v. g.: Si el posible experto marcó el número 8, éste se multiplica por 0,1 y se obtiene 0,8; luego, Kc = 0,8.
- Ka: coeficiente de argumentación. Este coeficiente se autoevalúa en alto (A), medio (M) o bajo (B) como el grado de influencia de las fuentes siguientes: análisis teóricos realizados por el posible experto, su experiencia obtenida, trabajos de autores nacionales, trabajos de autores extranjeros, su propio conocimiento del estado del problema en el extranjero y su intuición (Anexo 1, Tabla 2). Veamos la tabla 2 de este anexo:
| Fuentes de argumentación | Grado de influencias de cada una de las fuentes | ||
| A (alto) | M (medio) | B (bajo) | |
| Análisis teóricos realizadas por usted. | (0,4) | (0,3) | (0,2) |
| Su experiencia obtenida. | (0,5) | (0,4) | (0,2) |
| Trabajos de autores nacionales. | (0,025) | (0,025) | (0,025) |
| 0.025 | 0.024 | 0.022 | |
| Trabajos de autores extranjeros. | (0,025) | (0,025) | (0,025) |
| 0.025 | 0.024 | 0.022 | |
| Su propio conocimiento del estado del problema en el extranjero. | (0,025) | (0,025) | (0,025) |
| 0.025 | 0.024 | 0.022 | |
| Su intuición | (0,025) | (0,025) | (0,025) |
| 0.025 | 0.024 | 0.022 | |
Fuente: Campistrous, 1998.
Al observar la tabla, en el aspecto: fuentes de argumentación, las propuestas revisadas (Campistrous, 1998), (Valdés, 1999)…, no distinguen entre las categorías de Alto, Medio y Bajo, a partir del indicador: trabajos con autores nacionales (observe los valores que aparecen en la parte superior entre paréntesis y no marcados en negrita, a partir del indicador trabajos de autores nacionales), adjudicándole la misma puntuación a cada rubro; por lo que se propone su diferenciación a partir de los valores que aparecen debajo de la barra en negrita, para que queden bien diferenciadas cada una de las categorías de las fuentes de argumentación.
De acuerdo con los puntos obtenidos, este coeficiente recibe el valor de 0.796, (suma de cada rubro de este indicador, vea en el Anexo 1, Tabla 2, valores marcados con una `X´). Entonces el coeficiente de competencia de este experto estará dado por: K = ½ (0,8 + 0,796) = 0, 798 ≈ 0,8, que en este caso es alto, debido a que:
- Sí 0,8 £ K £ 1; entonces, el coeficiente de competencia es alto.
- Sí 0,5 £ K < 0,8: coeficiente de competencia medio
- Sí K < 0,5: coeficiente de competencia bajo
Es importante aclarar que los valores de cada uno de los rubros de la segunda tabla del anexo 1 son de interés del investigador, por lo que no deben de aparecer en la misma.
Para los efectos de esta encuesta se determinó excluir a 25 personas como posibles expertos por alcanzar un bajo coeficiente de competencia (muchos fueron profesores de la Educación Técnica y Profesional con mucha experiencia, pero les faltaban otros requisitos). Por lo que quedaron 25 expertos.
6. ¿Qué es el Modelo Torgerson?
Existen distintas técnicas y modelos para la valoración de consensos para los expertos, que pueden ser estudiados en el Folleto del Grupo de Técnicas de Dirección (Getedi) (Zayas, 1990)
y otros manuales, que por razones obvias de alcance de este trabajo no se van analizar; por lo que se considera conveniente explicar un método y modelo matemático muy útil, cuando las escalas empleadas en los instrumentos aplicados a los expertos sean ordinales: Modelo Matemático Torgerson, que es una variante del método Thurstone (Moráguez, 2001).
Ya se analizó que una de las desventajas del método (Delphi) radica en la subjetividad de los criterios emitidos, por lo que para tratar de resolver este problema, se opta por emplear este modelo matemático, que permite, no sólo asignar un valor de escala a cada indicador, sino determinar límites entre cada categoría y, de esta forma, se pueden obtener los límites reales (asignado por un número real), entre las categorías ordinales y sus correspondientes a escala de intervalo (números reales), entre cada uno de los rangos que componen los criterios evaluativos dados por los expertos, y de esta forma se pueden conocer con precisión cuáles son los límites reales de cada categoría; es decir, hasta qué valores reales se puede considerar que la variable es indispensable, muy útil, etc.
Con el modelo Torgerson se trata de dar objetividad a los criterios de los expertos u otro personal encuestado, al convertir la escala ordinal en escala de intervalo (de cualitativo a cuantitativo).
Para lograr la objetividad, a partir de los criterios subjetivos, el modelo se apoya en dos leyes de la psicología social: Ley de los Juicios Comparativos y la Ley de los Juicios Categóricos (Campistruos, 1998), (Moráguez, 2001). Además se sustenta en los presupuestos siguientes:
1) Cada objeto (indicador) se corresponde con la dimensión subjetiva de una variable aleatoria distribuida normalmente, cuya media, m, es el valor de escala de ese objeto. Todas las varianzas son iguales.
2) Cada límite de categoría se corresponde con la dimensión subjetiva de una variable aleatoria distribuida normalmente, cuya media, t, es el valor de escala de ese límite. Todas las variables son iguales.
3) Las variables aleatorias que representan tanto a los objetos como a los límites, son independientes. Una variable no puede contener valores de otra.
4) Regla de decisión: un objeto a pertenece a la k-ésima categoría cuando su valor de escala x, está entre los valores de los límites de orden k-1 y k. Esto regla deja bien definida la frontera entre cada una de las categorías asumidas para los indicadores. (Campistrous, op. cit.), (Moráguez, op. cit).
Este modelo permite convertir los juicios ordinales, emitidos por expertos independientes, acerca de los indicadores, en un instrumento que expresa su posición relativa en un continuo; o sea, permite llevar las escalas ordinales a escala de intervalo (números reales) y de esta forma conocer los límites, en valores reales, en que se encuentra cada categoría; por ejemplo:
Excelente, Muy Bien…; o de 5, 4, 3…
7. Metodología para aplicar el Modelo Matemático Torgerson
1) Operacionalización de las variables a emplear
Es importante aclarar que cuando se solicite información a los expertos acerca de estimar la posible categorización de cada uno de los indicadores o variables propuestas, es necesario que el investigador deje bien definidos los conceptos que asume para cada variable, así como establecer su operacionalización, que no es más que disponer los distintos parámetros e indicadores que permitan medir la variable en el sujeto (Tena, 1996), para posibilitar una mejor comprensión y evaluación de los juicios emitidos por los expertos.
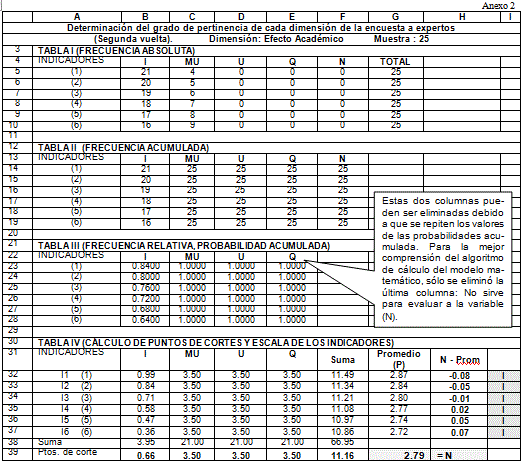
Para comprender mejor el método, se tomó como referente la propuesta de este autor de su tesis de maestría, que por el método de expertos determinó los 24 indicadores, distribuidos en seis dimensiones, sugeridos para evaluar la eficiencia externa o el impacto educacional de las escuelas politécnicas (Moráguez, 2001). De estos indicadores se tomó como referente de análisis la dimensión Efecto Académico, constituida por seis indicadores.
Le recordamos al lector que las palabras que aparecen subrayadas y en color azul son hipervínculos creados para que el mismo haciendo control + clic pueda ir directamente al anexo, tabla, etc.
En el anexo 2 puede observarse cómo quedó la pertinencia de cada indicador para medir las variables propuestas, para la segunda vuelta de los expertos, en la dimensión Efecto Académico.
En las columnas aparecen las categorías ordinales para medir las variables dadas en: Indispensable (I), Muy Útil (MU), Útil (U), Quizás Sirva (Q) y No Sirve (N). Fíjese que a cada indicador se le hizo corresponder un número consecutivo (filas) para facilitar el trabajo de compilación y estadística de los mismos, que por razones obvias no se detallarán en este trabajo.
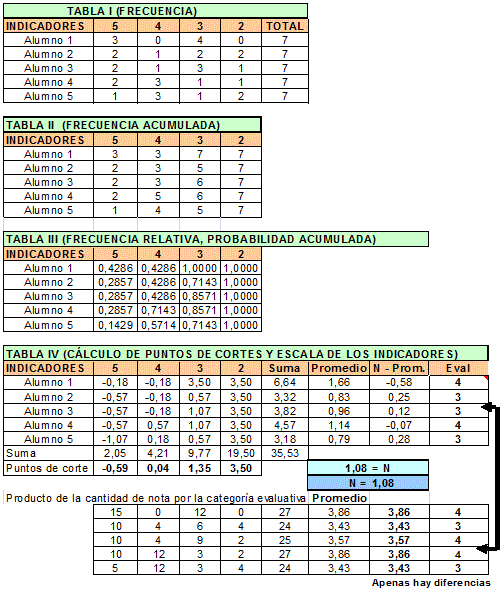
2) Compilación de la frecuencia absoluta
Le recordamos al interesado que haciendo click en los hipervínculos marcados puede desarrollar el cálculo en Excel de este mismo ejemplo.
Como resultado de la compilación de los instrumentos aplicados a los expertos se hace una tabla (Anexo 2, Tabla I) en Excel, y en ella se lleva los criterios de los expertos en relación con los indicadores correspondientes a la dimensión Efecto Educativo. Las columnas reflejan los totales de cada categoría.
3) Determinación de la frecuencia acumulada
A cada indicador se le determina su frecuencia acumulada, así: al indicador 1 (Anexo 2, Tabla I) 21 expertos lo consideraron Indispensable y 4 Muy Útil, por lo que en la frecuencia acumulada (Anexo 2, Tabla II) que aparece en el rubro Muy Útil es de 25 (casilla C14); por consiguiente están incluidos los 21, que lo ven como Indispensables (casilla B14), y los 4 Muy Útil. De forma análoga se halló cada uno y se completó la tabla según Anexo 2.
4) Determinación de la frecuencia relativa acumulada o probabilidad acumulada
Se determina la matriz de probabilidades acumulada con cuatro cifras decimales (Anexo II, Tabla III), que resulta de dividir cada acumulado entre el número de la muestra, en este caso 25; por ejemplo, si dividimos 21 (valor de la casilla B14) entre 25, resulta la probabilidad acumulada 0,8400 (casilla B23). De esta forma se completa dicha tabla.
Es importante observar cómo a partir de la categoría en que se repite la probabilidad 1, que en este caso es la categoría de Muy Útil, no es necesario completar las siguientes columnas, porque ya acumuló la máxima probabilidad, lo que quiere decir que este indicador es considerado, como mínimo de Muy Útil. Para comprender mejor el paso siguiente, se ha eliminado solamente la última columna: No Sirve para medir la variable (N).
5) Cálculo de los puntos de cortes y escala de los indicadores (Anexo 2, Tabla IV)
5.1 Determinación de los valores normales estándar inversos
a) Método manual para buscar los valores
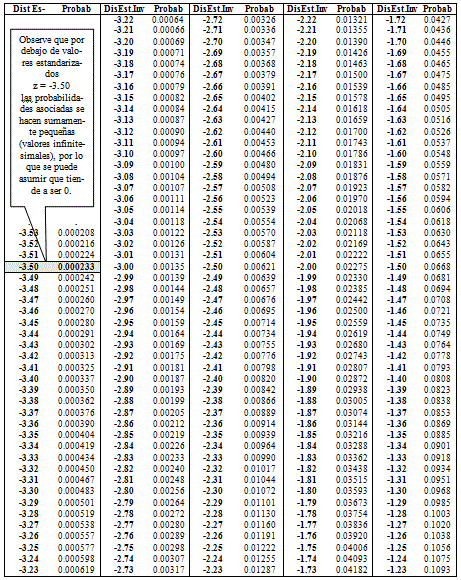
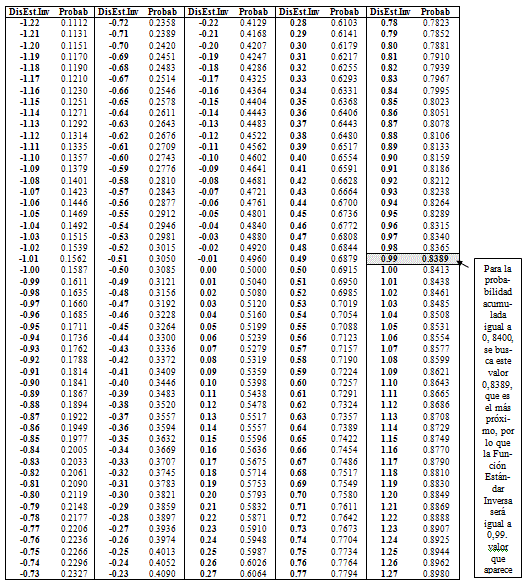
Para determinar los valores normales estándar inversos de las probabilidades acumuladas de cada indicador, se localizan los valores en las tablas del anexo 3 (hoja 1 hasta la 3, que no es más que la tabla de la distribución estándar), acorde con la probabilidad asociada y se procede como sigue:
Se busca en el anexo 3 el valor más próximo de la curva Normal Estándar de la probabilidad acumulada 0,8400 (tabla III, anexo 2). Se aclara que en Excel se le llama a esta función estándar inversa porque conocido el valor de la probabilidad acumulada se debe buscar los valores estandarizados de la tabla.
En el anexo 3, hoja 2 aparece el valor más próximo de la probabilidad acumulada (aparece marcado) de 0, 8389 y le corresponde el valor estándar inverso de 0,99; valor que se coloca en la casilla B32 de la tabla IV del anexo 2. Se procede de igual forma para el resto de los valores de las probabilidades acumuladas hasta la casilla E28.
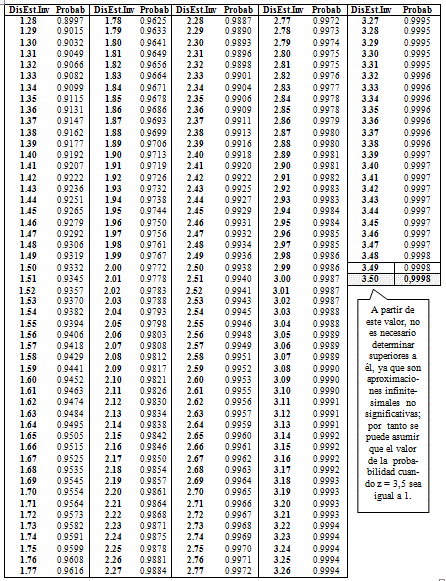
Es importante saber que cuando la probabilidad acumulada sea igual a 1, le corresponde el valor estándar inverso de 3,5 y que este valor se hace asintótico a partir de 3,49, por lo que en la práctica se toma igual a 3.5, para trabajar con ambos extremos iguales; es decir, si por el contrario la probabilidad acumulada es igual a 0, entonces el valor estándar inverso se asume igual a -3,5 (Anexo 3, hoja 3 y hoja 1 respectivamente); observe en la tabla (Anexo III Hoja 1) que las probabilidades, a partir de z= -3,5 toma valores sumamente pequeños (infinitesimales), por lo que se puede considerar que para valores menores de -3.5 se asuma la probabilidad acumulada igual a 0 y es, además un recurso fácil para asociar las probabilidades máximas y mínimas a un mismo valor absoluto (3.5); Luego si Z = -3.5, la probabilidad para este valor = 0 (La mínima); por el contrario, si Z = 3.5, la probabilidad asociada a este valor es 1 (la máxima).
Resulta oportuno aclarar al lector, que los valores máximo y mínimos de la función normal muchos autores difieren en ellos; por ejemplo: Murray (1961) toma como valor máximo 3,99 y mínimo -3,99; Freud (1977) asume 3,09 y -3.09; Douglas (1996) toma ± 3, 99; Devore (2000) asume ± 3,49.
Pero como todos estos valores son asintóticos a partir de ± 3, 5 es por ello que este autor lo asume así, por ser hasta más fácil de recordar,De esta forma se pueden encontrar los valores de esta función de forma manual y llenar la tabla IV (Anexo 2). b) Método automático para buscar los valores de la función estándar inversaEstos valores se hallan de forma automática a través del Microsoft Excel del Windows. Para determinar de forma automática cada uno de dichos valores se debe situar en la casilla donde se va a insertar el valor de la Función Normal Estándar Inversa (Casilla B39 de la hoja 1 de Excel, que en el ejemplo de este trabajo corresponde a la casilla B32, del anexo 2.
Una vez situado en dicha casilla, se debe especificar en la barra de cálculo, buscar la Función Estándar Inversa correspondiente a la probabilidad acumulada 0,8400 (casilla B31 de la Tabla III, anexo 2), pero se debe especificar que cuando la probabilidad acumulada sea igual a 0, la función inversa tome el valor -3,5 (valor marcado en gris de la Hoja 1, anexo 3); por el contrario, si la probabilidad acumulada tomase el valor de 1, entonces su Función Estándar Inversa asumirá el valor de 3, 50 (último valor de la Hoja 3, anexo 3). Esto se programa en la barra de fórmula del Excel: =SI(B23=0,-3.5,SI(B23=1,3.5,(DISTR.NORM.ESTAND.INV(B23))))
Observe que la casilla que se hace referencia es la B23 (tabla III, anexo 2), porque es la primera casilla a la que se debe determinar la Función Estándar Inversa de la probabilidad acumulada.
Así se programa esta función (en Excel) que permite determinar los valores inversos de cada probabilidad asociada, de manera tal que cuando esta probabilidad sea igual a cero, entonces la computadora lo asuma como una respuesta lógica de verdad y devuelva el valor -3.50, y cuando sea la probabilidad 1, devuelva el valor lógico de 3.50.
Esto lo puede observar haciendo click en la barra de cálculo de Excel haciendo clic en el hipervínculo siguiente:
Llamar ejercicio en Excel.Se aclara que según la metodología planteada por el modelo, se elimina(n) la(s) última(s) columna(s) cuyos valores sean iguales a 3,5, debido a que cuando se determine el último punto de corte, indicará que todos los valores mayores que ese valor corresponderá(n) a la(s) variable(s) eliminada(s) (presupuesto número 4 del método); esto último se comprenderá mejor en el epígrafe siguiente. Por tal razón sólo aparecen cuatro columnas con las escalas I, MU, U y Q. (Anexo 2, Tabla IV); se insiste que por razones de comprender mejor el paso siguiente, no se han eliminado las columnas de U y Q, (se puede hacer) ya que el valor máximo de la Distribución Normal llega hasta 3, 5 (probabilidad 1,000).5.2 Búsqueda de los puntos de corteUna vez determinada cada imagen por la Curva Normal Estándar Inversa, se suma cada columna y cada fila (Anexo 2, Tabla IV); se promedian las filas: las sumas de las filas se divide entre cuatro, que es el número de columnas que se hace corresponder a cada escala, y el resultado se asigna a la columna Promedio (P, casilla G32). Si se hubiesen eliminado las columnas U y Q, entonces se dividiría por dos (números de columnas que quedaron: I y MU). Se procede de igual forma con las columnas donde aparecen las escalas de I, MU, U y Q, pero al resultado de la suma de la columna se divide entre el número de indicadores (en este caso 6) y se halla el promedio de cada columna (Anexo 2, Tabla IV, fila 39).
A los valores que resultan de las operaciones anteriores se les llama puntos de corte, y determinan los valores del intervalo en que van a estar comprendidas las variables cualitativas (I, MU, U y Q) (ver rayo numérico determinado con los valores de los intervalos en la parte inferior del Anexo 2).
Ahora se promedia los valores de los puntos de cortes, que no son más que los promedios de cada categoría (columna), por lo que se obtiene el promedio de promedio, llamado valor límite N.
Para saber en qué rango verdaderamente está la variable, se le resta al valor límite N el valor promedio de cada fila P. Por ejemplo: para la primera fila o indicador No. 1 (1), se le resta al valor límite N (promedio de promedio) (2,79) el valor promedio de esta fila P (2,87, casilla G32) (Anexo 2, Tabla IV) y su resultado aparece en la columna N-P (-0,08, casilla H32). Como este valor está por debajo de 0,66 (casilla B39), que es el punto de corte o límite superior para la categoría de Indispensable (I).
Por lo que los expertos consideraron que esta categoría era indispensable para el indicador (1).
De manera análoga se determina cada rango del resto de los indicadores, cuyos resultados se puede apreciar en la tabla del anexo antes citado.
8. Determinación del nivel de consenso de la primera vuelta.
El nivel de consenso (C) se determina por la expresión: ; donde:
Donde…
C: coeficiente de concordancia.
Regla de decisión: Sí C ³ 75 %, se considera que hay consenso.
Vn: Votos negativos; Vt: Votos totales.
En caso de que no haya consenso entre los expertos C< 75 %, se deberá hacer otra vuelta de consulta, realizándose las modificaciones y aclaraciones necesarias que permitan obtener consenso a las nuevas modificaciones y adecuaciones de la nueva propuesta de estos expertos.
Como se observa en el Anexo 2, Tabla IV, los 25 expertos consideraron que los seis indicadores propuestos, para evaluar el efecto educativo resultaron indispensables (I), con un elevado grado de relevancia; ya que no hubo votos negativos (Vn = 0); los votos totales fueron 25, que coincidieron con los positivos (Vt = 25), entonces: C = (1 – 0/25) • 100 = 100 %. De esta forma se determinó el resto de los 24 indicadores en las seis dimensiones propuestas.
A manera de conclusión se puede expresar que el método Delphi o método de expertos, es muy valioso para la toma de decisiones, y que en la actualidad se emplea ampliamente en las empresas líderes como método de dirección e investigaciones de índole general, debido a la participación que se le conceden a toda una serie de expertos, lo que permite obtener opiniones informadas con un alto nivel de competencia, para finalmente arribar a consensos con relación a las problemáticas planteadas.
Uno de los elementos más importantes de este método radica en la minuciosa selección de los posibles expertos a partir de una bolsa o relación, de los que se supone pudieran serlos, con la aplicación de los instrumentos ya analizados y que permitan garantizar el anonimato: que cada experto no sepa quién es su igual, para así evitar efectos de halo, entre otros.
Por lo general, cuando se trata de evaluar o determinar la pertinencia de indicadores expresados en escala ordinal, se debe aplicar el modelo matemático Torgerson, (ya explicado su empleo en este trabajo) modificación del modelo Thurstone, que permite llevar las escalas ordinales a escala de intervalo y así conocer en qué intervalo numérico se encuentran cada una de dichas categorías cualitativas para conocer el grado de pertinencia de los indicadores, variantes metodológicas, y en general las propuestas realizadas.
Este no es el único método que existe para compilar los resultados de las opiniones de los expertos; al contrario, este método puede, y debe ser combinado con otros que coadyuven a obtener un mejor consenso de las formulaciones efectuadas.
Anexo 1
Consulta a Expertos
(Método Delphi)
Usted ha sido seleccionado como posible experto para ser consultado respecto al grado de relevancia de un conjunto de indicadores que presumiblemente deben servir para evaluar la eficiencia externa o impacto educacional de las escuelas politécnicas industriales en la provincia de Holguín, con vista a la investigación que se está llevando a cabo como tesis de una maestría en Planeamiento, Administración y Supervisión de Sistemas Educativos por el Instituto Pedagógico Latinoamericano y Caribeño (IPLAC).
Es necesario, antes realizarle la consulta correspondiente como parte del método empírico de investigación: “consulta a expertos”, determinar su coeficiente de competencia en este tema a los efectos de reforzar la validez del resultado de la consulta que se realizará. Por otra razón se le ruega que responda las siguientes preguntas de la forma más objetiva que le sea posible. ¡Gracias!
1. Marque con una cruz (X), en la tabla siguiente, el valor que se corresponde con el grado de conocimiento que usted posee sobre el tema “determinación de indicadores para evaluar la calidad de la educación”. (Considérese que la escala que se le presenta es ascendente, es decir, el conocimiento sobre el tema referido va creciendo desde 0 hasta 10).
Tabla 1
| 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| X |
Fuente: (Campistrous, 1998; 19).
2. Realice una autoevaluación del grado de influencia que cada una de las fuentes, que se le presenta a continuación, ha tenido en su conocimiento y criterios sobre la determinación de indicadores para evaluar la calidad de la educación. Para ello marque con una cruz (X), según corresponde, en: A (al-to), M (medio o B (bajo).
Tabla 2
| Fuentes de argumentación | Grado de influencias de cada una de las fuentes | ||
| A (alto) | M (medio) | B (bajo) | |
| Análisis teóricos realizadas por usted. | (0,4) | (0,3)X | (0,2) |
| Su experiencia obtenida. | (0,5) | (0,4)X | (0,2) |
| Trabajos de autores nacionales. | (0,025) | (0,024)x | (0,022) |
| Trabajos de autores extranjeros. | (0,025) | (0,024) | (0,022)x |
| Su propio conocimiento del estado del problema en el extranjero. | (0,025)x | (0,024) | (0,022) |
| Su intuición | (0,025)x | (0,024) | (0,022) |
Anexo 2
 Fuente: (Moráguez, 2001, anexo 19)
Fuente: (Moráguez, 2001, anexo 19)
Correspondencia entre las categorías cualitativas y el rayo numérico
Observe que los puntos de corte determinan hasta donde llegan los límites de intervalo para cada categoría. En este caso arrojó que todos los valores menores o iguales a 0,66 caen en la categoría de Indispensable y el resto en muy útil.
Tabla de distribución estándar (Anexo 3 Hoja 1)
Fuente: Función Estándar Inversa de Excel 2000
Tabla de distribución estándar Anexo 3 Hoja 2
 Fuente: Función Estándar Inversa de Excel 2000
Fuente: Función Estándar Inversa de Excel 2000
Tabla de distribución estándar Anexo 3 Hoja 3
 Fuente: Función Estándar Inversa de Excel 2000
Fuente: Función Estándar Inversa de Excel 2000
Ejemplo de cómo aplicar el modelo matemático Torgerson para dar la evaluación final de un grupo de estudiantes. A un grupo de estudiantes se le desea su evaluación final en una signatura, teniendo en cuenta todas las evaluaciones cualitativas efectuadas en el semestre y para ello se aplica este modelo matemático.
Bibliografía
1. CAMPISTROUS PÉREZ, L. Indicadores e investigación educativa / Luis Campistrous, Celia Rizo Cabrera. — La Habana, 23 de agos., 1998. — 23p. — (Material inédito).
2. FRIEDRICH, W. Métodos de la investigación social marxista-leninista. Edit. Ciencias Sociales, La Habana, 1988. 325 p.
3. MORÁGUEZ IGLESIAS, A. Propuesta de indicadores para evaluar la eficiencia externa de las escuelas politécnicas industriales de la provincia de Holguín . — 2001. – 105 p. Tesis para optar por el título de Máster en Planeamiento, Administración y Supervisión de Sistemas Educativos. — IPLAC : Instituto Pedagógico Latinoamericano y Caribeño. La Habana, 2001.
4. TENA SUCK, E., A. Manual de investigación experimental: elaboración de tesis. — Edit. Plaza y Valdés, Mexico, 1996. 82 p.
5. THURSTONE, L. L. The Metod of paired Comparisson for Social Values (El método de comparación de pares para valores sociales). En : J. Abn. Soc. Psychol. No. 21, 1927. 14 p.
6. Theory of Attitude Measurement (Teoría de la medición de actitudes). En : Psychol No. 36, 1929. 14 p.
7. TORGERSON, W. S. Multidimensional Acalling: I. Theory and Metod (Escala multidimensional: I Teoría y método). En : Psychometrika. No 17, 1952. 12 p.
8. Multidimensionalk Scalling of Similitary (Escala multidimensional de semejanza) En : Psychometrika. No 30, 1965. 15 p.
9. ZAYAS MIRANDA, E. El proceso de las decisiones y de soluciones de problemas. Grupo Técnicas de Dirección GETEDI. Serie: Temas de dirección. No 004, ISTH, Holguín, 1990. 70 p.
[1] Este método fue creado en la RAND CORPORATION de USA en la década de 1940, por T. J. Cordon y Olaf Helmer y se publicó en 1964 (Zayas, 1990; 30).