Las anualidades son una serie de pagos iguales, realizados a una misma tasa de interés en periodos de tiempo iguales.
El estudio de las anualidades permite introducir a las personas interesadas en el área de las matemáticas financieras en el análisis de la estructura financiera de la empresa. Se explica la parte teórica y se complementa con algunos ejercicios prácticos.
Los pagos que realiza la empresa y los ingresos que recibe son de vital importancia para la consolidación de la organización. Es por ello que se debe medir constantemente el valor de estos y la incidencia que tiene dentro del entorno empresarial.
Definición de anualidad
Una anualidad es una serie de pagos que cumple con las siguientes condiciones:
- Todos los pagos son de igual valor.
- Todos los pagos se hacen a iguales intervalos de tiempo.
- Todos los pagos son llevados al principio o al final de la serie a la misma tasa.
- El número de pagos debe ser igual al número de periodos.
Algunos términos empleados cuando se trata de anualidades:
- Renta: Es el pago periódico de igual valor.
- Periodo de renta: Es el tiempo que transcurre entre los pagos periódicos continuos.
- Plazo: El tiempo que transcurre entre el principio del primer periodo y el final del último periodo se denomina plazo de la anualidad y se representa por la letra n.
Clasificación de las anualidades
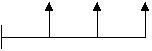
Anualidad Ordinaria o Vencida
Es aquella en la cual los pagos se hacen al final de cada periodo, por ejemplo el pago de salarios a los empleados, ya que primero se realiza el trabajo y luego se realiza el pago. Se representa así:
Valor de una anualidad ordinaria
Una anualidad tiene dos valores:
1. El valor final: Todos los pagos son traslados al final de la anualidad. El valor final se representa por el símbolo S n¬i en el cual la:
- S = Valor final.
- n¬ = Número de pagos.
- i = Tasa de interés
Otra simbología muy utilizada es (F/A, n, i) que significa valor futuro dada una anualidad de n periodos a la tasa i.
Para plantear la ecuación de valor, se aplica la fórmula:
S= p (1+i)n
A cada pago, pero, en cada caso, p= 1. El pago que está en el punto 1 se traslada por n-1 periodos, el que está en 2, por n-2 periodos y así sucesivamente, hasta que se llegue al pago que está en n el cual no se traslada por estar en la fecha focal, entonces se tiene:
(F/A, n, i)=S n¬i = (1 + i )n -1/ i
2. El valor presente: Este se representa por el símbolo a n¬i o por (P/A, n, i), que significa el presente de una anualidad en n periodos a la tasa i. Se representa por la fórmula:
(P/A, n, i)=a n¬i = 1 – (1 + i )-n / i
Ejemplo 1.
Un documento estipula pagos trimestrales de $80.000 durante seis años. Si este documento se cancela con un solo pago de A) Al principio o B) al final. Determinar $A y $S suponiendo un interés del 32% CT.
Solución: El número de pagos es n= 4 x 6= 24, R= $80.000
i= 32/4= 8% efectivo trimestral
A= 80.000 (P/A, 24, 8%)
A= 80.000* 1 – (1 +0.08 )-24 /0.08
A= 842.301
S= 80.000 (F/A, 24, 8%)
S= 80.000* (1 +0.08 )24 -1/ 0.08
S= 5.341.181
Ejemplo 2.
Una deuda de $50.000 se va a cancelar mediante doce pagos uniformes de $R c/u. Con una tasa del 2% efectivo para el periodo, hallar el valor de la cuota situando A) la fecha focal hoy y B) la fecha focal en doce meses.
Solución:
50.000= R a 12¬2%
R= 4727.98
50.000 (1.02)12 = R S 12¬2%
R= 4.727.98
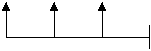
Anualidad Anticipada
En esta los pagos se hacen al principio del periodo, por ejemplo el pago mensual del arriendo de una casa, ya que primero se paga y luego se habita el inmueble. Se representa así:
Las anualidades anticipadas se representan por la ecuación:
¨sn¬i = S n¬i (1 + i ) Para valor final
ä n¬i = a n¬i (1 + i ) Para valor presente
La diéresis indica que es anticipado.
Ejemplo 3.
Una persona arrienda una casa en $50.000 pagaderos por mes anticipado. Sí tan pronto como recibe el arriendo lo invierte en un fondo que le paga el 2% efectivo mensual. ¿Cuál será el monto de sus ahorros al final del año?
Solución:
X= 50.000¨S 12¬2%(1.02)
X= 684.016.58
La diferencia entre las dos anualidades estriba en que la serie de la anualidad ordinaria empieza con 1 y termina con (1+i) n-1, en cambio la serie de la anualidad anticipada comienza con (1+i) y termina con (1+i)n
En la siguiente serie de videos se explica, a nivel teórico y práctico, el tema de las anualidades, tanto ordinarias o vencidas como anticipadas, además de las diferidas y las generales. Un buen complemento de aprendizaje para profundizar en este ítem de las matemáticas financieras. (7 videos, 1 hora y 27 minutos)
Bibliografía
BACA, Guillermo. «Ingeniería económica». Editorial educativa.
Sampayo, Leonardo. Manual de operaciones financieras. U. Externado.