El análisis matemático de las anualidades es muy importante para realizar las proyecciones financieras que la empresa necesita en el estudio de nuevos proyectos
Anualidades diferidas
Una anualidad diferida es aquella en que el primer pago se efectúa después de transcurrido cierto número de periodos.
Ejemplo 1
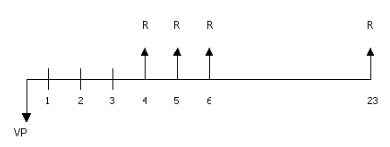
Una deuda de $800.000 se va a cancelar mediante 20 pagos trimestrales de $R cada uno. Si el primer pago se efectúa exactamente al año de haberse prestado el dinero, calcular R con una tasa del 36% CT.
Solución
Se observa que el primer pago está en el periodo 4 que corresponde al final del primer año. La anualidad debe comenzar en el punto 3 y terminar en el punto 23, además, su valor presente deberá trasladarse al punto 0 donde se ha puesto la fecha focal. La ecuación de valor será:
800.000 = R (1 – (1+0.9)-20/0.09)(1.09)-3
R = $113.492,69
Anualidades
- Ordinarias
- Vencidas
- Diferidas
- Perpetuas
- Generales
Anualidades perpetuas
Una anualidad que tiene infinito número de pagos, se denomina Anualidad infinita o perpetua, en realidad, las anualidades infinitas no existen, porque en este mundo todo tiene fin, pero, se supone que es infinita cuando el número de pagos es muy grande.
Este tipo de anualidades se presenta, cuando se coloca un capital y únicamente se retiran los intereses.
La anualidad perpetua se representa:
Obviamente, solo existe valor presente que viene a ser finito, porque el valor final será infinito
VP = Lim n–µ R (1- (1+i)-n)/i)
VP = R Lim n–µ 1-0/i
VP = R/i
Ejemplo 1
Hallar el valor presente de una renta perpetua de $10.000 mensuales, suponiendo un interés del 33% CM.
Solución
i = 33%/12
i = 2.75%
VP = R/i
VP = 10.000/0.0275
VP = 363.636,36
Anualidades generales
Las anualidades ordinarias y anticipadas son aquellas en que el periodo de interés coincide con el periodo de pago. En el caso de las anualidades generales los periodos de pago no coinciden con los periodos de interés, tales como una serie de pagos trimestrales con una tasa efectiva semestral.
Para realizar un análisis financiero confiable es necesario aplicar todas las herramientas necesarias y correctas en cada caso
Una anualidad general puede ser reducida a una anualidad simple, si hacemos que los periodos de tiempo y los periodos de interés coincidan, hay dos formas como se puede realizar:
1. La primera forma consiste en calcular pagos equivalentes, que deben hacerse en concordancia con los periodos de interés. Consiste en encontrar el valor de los pagos que, hechos al final de cada periodo de interés, sean equivalentes al pago único que se hace al final de un periodo de pago.
2. La segunda forma consiste en modificar la tasa, haciendo uso del concepto de tasas equivalentes, para hacer que coincidan los periodos de interés y de pago.
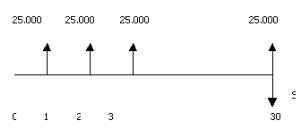
Ejemplo 1
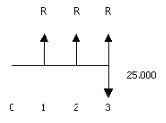
Hallar el monto de S de 30 pagos trimestrales de $25.000 cada uno suponiendo una tasa del 24% CM. realizándolo por los dos métodos.
Solución
1. A. Se reemplaza el pago de $25.000 al final de un trimestre, por pagos al final de cada mes así:
B. Entonces queda una anualidad simple, porque los pagos son mensuales de $R cada uno y la tasa de
i = 24%/12
i = 2%
C. Se tiene entonces que:
25.000 = R (1+0.02)3)-1/0.02
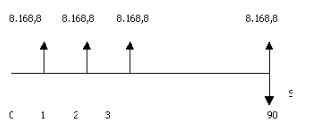
R = 8.168,87
D. El número de pagos mensuales será de 30 x 3 = 90, entonces S será:
S = 8.168,87 (1+0.02)90-1/0.02
S = 2.018.990
2. A. Se busca una tasa efectiva trimestral equivalente al 24% CM
(1+0.02)12 = (1+i)4
i = 6.1208% Efectivo trimestral
B. Se tiene entonces:
S = 25.000 (1+0.061208)30-1/0.061208
S = 2.018.990