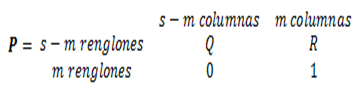Introducción
Dentro de esta investigación se planteó el objetivo de definir cada uno de los conceptos que integran el análisis de Markov, comenzando desde los más básicos hasta los más complejos, al igual el por qué es llamado así a dicho estudio, dándole este nombre por su autor (Markov) en este documento se plasma acerca de su biografía, así como todos sus logros que ejecutó.
Otro tema de suma importancia que hacemos mención, son las cadenas de Markov, que hacen referencia a una herramienta para analizar el comportamiento y el gobierno de determinados tipos de procesos estocásticos, esto es, procesos que evolucionan de forma no determinística a lo largo del tiempo en torno a un conjunto de estados.
Una cadena de Márkov, por tanto, representa un sistema que varía un estado a lo largo del tiempo, siendo cada cambio una transición del sistema.
Para tales cadenas, se hace el uso de diversos términos involucrados para un mejor entendimiento, como son: Los estados son la caracterización de la situación en que se halla el sistema en un instante dado, matriz de transición: Que es el arreglo numérico donde se condensa las probabilidades de un estado a otro. La matriz regular: es una matriz cuadrada que posee inversa. Estado recurrente: Un estado es recurrente si después de haber entrado a este estado, el proceso definitivamente regresa a ese estado, Matriz ergódica: Si los estados en una cadena son recurrentes, aperiódicos y se comunican entre si. Estados absorbentes: Una cadena de Márkov en la que uno o más estados es un estado absorbente, es una cadena de Márkov absorbente.
Todos estos temas se explican más a detalle y con mejor entendimiento dentro del documento.
Análisis de Markov
El análisis de Markov, llamado así por los estudios realizados por el ruso Andréi Andréyevich Márkov entre 1906 y 1907, sobre la secuencia de los experimentos conectados en cadena y la necesidad de descubrir matemáticamente los fenómenos físicos. La teoría de Markov se desarrolló en las décadas de 1930 y 1940 por A.N.Kolmagoron, W.Feller, W.Doeblin, P.Levy, J.L.Doob y otros.
El análisis de Markov es una forma de analizar el movimiento actual de alguna variable, a fin de pronosticar el movimiento futuro de la misma. Este método ha comenzado a usarse en los últimos años como instrumento de investigaciones de mercadotecnia, para examinar y pronosticar el comportamiento de los clientes desde el punto de vista de su lealtad a una marca y de sus formas de cambio a otras marcas, la aplicación de esta técnica, ya no solo se limita a la mercadotecnia sino que su campo de acción se ha podido aplicar en diversos campos.
Andréi Márkov
Andréi Andréyevich Márkov: (14 de junio de 1856 – 20 de julio de1922) fue un matemático ruso conocido por sus trabajos en la teoría de los números y la teoría de probabilidades.
Márkov nació en Riazán, Rusia. Antes de los 10 años su padre, un funcionario estatal, fue trasladado a San Petersburgo donde Andréi entró a estudiar en un instituto de la ciudad. Desde el principio mostró cierto talento para las matemáticas y cuando se graduó en 1874 ya conocía a varios matemáticos de la Universidad de San Petersburgo, donde ingresó tras su graduación. En la Universidad fue discípulo de Chebyshov y tras realizar sus tesis de maestría y doctorado, en1886 accedió como adjunto a la Academia de Ciencias de San Petersburgo a propuesta del propio Chebyshov. Diez años después Márkov había ganado el puesto de académico regular. Desde 1880, tras defender su tesis de maestría, Márkov impartió clases en la Universidad y, cuando el propio Chebyshov dejó la Universidad tres años después, fue Márkov quien le sustituyó en los cursos de teoría de la probabilidad. En 1905, tras 25 años de actividad académica, Márkov se retiró definitivamente de la Universidad, aunque siguió impartiendo algunos cursos sobre teoría de la probabilidad.
A parte de su perfil académico, Andréi Márkov fue un convencido activista político. Se opuso a los privilegios de la nobleza zarista y llegó a rechazar las condecoraciones del propio zar en protesta por algunas decisiones políticas relacionadas con la Academia de Ciencias. Hasta tal punto llegó su implicación en la política que llegó a ser conocido con el sobrenombre de «el académico militante».
Márkov arrastró durante toda su vida problemas relacionados con una malformación congénita en la rodilla que le llevaría varias veces al quirófano y que, con el tiempo, fue la causa de su muerte cuando el 20 de julio del año 1922 una de las muchas operaciones a las que se sometió le produjo una infección generalizada de la que no pudo recuperarse.
Aunque Márkov influyó sobre diversos campos de las matemáticas, por ejemplo en sus trabajos sobre fracciones continuas, la historia le recordará principalmente por sus resultados relacionados con la teoría de la probabilidad. En 1887 completó la prueba que permitía generalizar el teorema central del límite y que ya había avanzado Chebyshov. Pero su aportación más conocida es otra.
Su trabajo teórico en el campo de los procesos en los que están involucrados componentes aleatorios (procesos estocásticos) darían fruto en un instrumento matemático que actualmente se conoce como cadena de Márkov: secuencias de valores de una variable aleatoria en las que el valor de la variable en el futuro depende del valor de la variable en el presente, pero es independiente de la historia de dicha variable. Las cadenas de Márkov, hoy día, se consideran una herramienta esencial en disciplinas como la economía, la ingeniería, la investigación de operaciones y muchas otras.
Cadenas de Markov
Las cadenas de Márkov son una herramienta para analizar el comportamiento y el gobierno de determinados tipos de procesos estocásticos, esto es, procesos que evolucionan de forma no determinística a lo largo del tiempo en torno a un conjunto de estados.
Una cadena de Márkov, por tanto, representa un sistema que varía un estado a lo largo del tiempo, siendo cada cambio una transición del sistema. Dichos cambios no están predeterminados, aunque sí lo está la probabilidad del próximo estado en función de los estados anteriores, probabilidad que es constante a lo largo del tiempo (sistema homogéneo en el tiempo). Eventualmente, es una transición, el nuevo estado puede ser el mismo que el anterior y es posible que exista la posibilidad de influir en las probabilidades de transición actuando adecuadamente sobre el sistema (decisión).
Conceptos básicos
Para el estudio de las cadenas de Márkov, deben tenerse en cuenta algunos conceptos claves como los siguientes:
Estados
El estado de un sistema en un instante t es una variable cuyos valores solo pueden pertenecer al conjunto de estaos en el sistema. El sistema modelizado por la cadena, por lo tanto, es una variable que cambia con el valor del tiempo, cambio al que llamamos transición.
Matriz de transición
Los elementos de matriz representan la probabilidad de que el estado próximo sea el correspondiente a la columna si el estado actual es el correspondiente a la fila.
Posee 3 propiedades básicas:
- La suma de las probabilidades de los estados debe ser igual a 1.
- La matriz de transición debe ser cuadrada.
- Las probabilidades de transición deben estar entre 0 y 1.
Distribución actual (Vector Po): Es la manera en la que se distribuyen las probabilidades de los estados en un periodo inicial, (periodo 0). Esta información te permitirá averiguar cuál será la distribución en periodos posteriores.
Estado estable: Se puede decir que el estado estable es la distribución de probabilidades que en cierto punto quedará fija para el vector P y no presentará cambios en periodos posteriores.
Por consiguiente un estado es recurrente si y solo si no es transitorio.
Ejemplo:
Suponga que hay s-m estados transitorios (t1, t2,…, ts-m) y m estado absorbentes (a1, a2,…, am), se escribe la matriz de probabilidades de transición P como sigue:
Conclusión
Para concluir podemos decir que las cadenas de Markov son una herramienta para analizar el comportamiento y el gobierno de determinados tipos de procesos estocásticos, esto es, procesos que evolucionan de forma no determinística a lo largo del tiempo en torno a un conjunto de estados.
Que para su elaboración requieren del conocimiento de diversos elementos como son el estado y la matriz de transición.
Dichos elementos fueron descubiertos por su creador Markov, el cual realizó una secuencia de experimentos conectados en cadena y la necesidad de descubrir matemáticamente los fenómenos físicos
Este método es muy importante, ya que ha comenzado a usarse en los últimos años como instrumento de investigaciones de mercadotecnia, para examinar y pronosticar el comportamiento de los clientes desde el punto de vista de su lealtad a una marca y de sus formas de cambio a otras marcas, la aplicación de esta técnica, ya no solo se limita a la mercadotecnia sino que su campo de acción se ha podido aplicar en diversos campos.
Esperemos que este artículo sea de gran utilidad y que los conceptos contenidos queden explicados de manera clara.
Referencias
- Pérez, J. (2011, 3 de Junio). Andrei Markov. Recuperado de http://investigacindeoperaciones.html
- Morales, L. (2011, 2 de Junio). Cadenas de Markov. Recuperado de: http://io2-ingindustrial.blogspot.com/2011/06/cadenas-de-markov.html